Выбор вида уравнения регрессии
Задача определения функциональной зависимости, наилучшим образом описывающей ЭД, связана с преодолением ряда принципиальных трудностей. В общем случае для стандартизованных данных функциональную зависимость показателя от параметров можно представить в виде
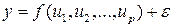 , (7.5)
, (7.5)
где f – заранее не известная функция, подлежащая определению;
ε - ошибка аппроксимации ЭД.
Указанное уравнение принято называть выборочным уравнением регрессии y на u. Это уравнение характеризует зависимость между вариацией показателя и вариациями факторов. А мера корреляции измеряет долю вариации показателя, которая связана с вариацией факторов. Иначе говоря, корреляцию показателя и факторов нельзя трактовать как связь их уровней, а регрессионный анализ не объясняет роли факторов в создании показателя.
Еще одна особенность касается оценки степени влияния каждого фактора на показатель. Регрессионное уравнение не обеспечивает оценку раздельного влияния каждого фактора на показатель, такая оценка возможна лишь в случае, когда все другие факторы не связаны с изучаемым. Если изучаемый фактор связан с другими, влияющими на показатель, то будет получена смешанная характеристика влияния фактора. Эта характеристика содержит как непосредственное влияние фактора, так и опосредованное влияние, оказанное через связь с другими факторами и их влиянием на показатель.
В регрессионное уравнение не рекомендуется включать факторы, слабо связанные с показателем, но тесно связанные с другими факторами. Не включают в уравнение и факторы, функционально связанные друг с другом (для них коэффициент корреляции равен 1). Включение таких факторов приводит к вырождению системы уравнений для оценок коэффициентов регрессии и к неопределенности решения.
Функция f должна подбираться так, чтобы ошибка ε в некотором смысле была минимальна. Существует бесконечное множество функций,описывающих ЭД абсолютно точно (ε = 0), т.е. таких функций, которые для всех значений параметров uj,2 , uj,3 , …, uj,т принимают в точности соответствующие значения показателя yi , i =1, 2, …, п. Вместе с тем, для всех других значений параметров, отсутствующих в результатах наблюдений, значения показателя могут принимать любые значения. Понятно, что такие функции не соответствуют действительной связи между параметрами и показателем.
В целях выбора функциональной связи заранее выдвигают гипотезу о том, к какому классу может принадлежать функция f, а затем подбирают "лучшую" функцию в этом классе. Выбранный класс функций должен обладать некоторой "гладкостью", т.е. "небольшие" изменения значений аргументов должны вызывать "небольшие" изменения значений функции (ЭД содержат некоторые ошибки измерений, а само поведение объекта подвержено влиянию помех, маскирующих истинную связь между параметрами и показателем).
Простым, удобным для практического применения и отвечающим указанному условию является класс полиномиальных функций
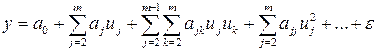 (7.6)
(7.6)
Для такого класса задача выбора функции сводится к задаче выбора значений коэффициентов a0 , aj , ajk , …, ajj , … . Однако универсальность полиномиального представления обеспечивается только при возможности неограниченного увеличения степени полинома, что не всегда допустимо на практике, поэтому приходится применять и другие виды функций.
Частным случаем, широко применяемым на практике, является полином первой степени или уравнение линейной регрессии
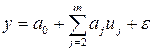 . (7.7)
. (7.7)
Это уравнение в регрессионном анализе следует трактовать как векторное, ибо речь идет о матрице данных
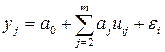 , i =1, 2, … , n. (7.8)
, i =1, 2, … , n. (7.8)
Обычно стремятся обеспечить такое количество наблюдений, которое превышало бы количество оцениваемых коэффициентов модели. Для линейной регрессии при п > т количество уравнений превышает количество подлежащих определению коэффициентов полинома. Но и в этом случае нельзя подобрать коэффициенты таким образом, чтобы ошибка в каждом скалярном уравнении обращалась в ноль, так как к неизвестным относятся аj и ei, их количество n + т – 1, т.е. всегда больше количества уравнений п. Аналогичные рассуждения справедливы и для полиномов степени, выше первой.
Для выбора вида функциональной зависимости можно рекомендовать следующий подход:
· в пространстве параметров графически отображают точки со значениями показателя. При большом количестве параметров можно строить точки применительно к каждому из них, получая двумерные распределения значений;
· по расположению точек и на основе анализа сущности взаимосвязи показателя и параметров объекта делают заключение о примерном виде регрессии или ее возможных вариантах;
· после расчета параметров оценивают качество аппроксимации, т.е. оценивают степень близости расчетных и фактических значений;
· если расчетные и фактические значения близки во всей области задания, то задачу регрессионного анализа можно считать решенной. В противном случае можно попытаться выбрать другой вид полинома или другую аналитическую функцию, например периодическую.
Дата добавления: 2015-05-05; просмотров: 1492;
