Метод моментов. Метод предложен К. Пирсоном в 1894 г

Метод предложен К. Пирсоном в 1894 г. Сущность метода:

· выбирается столько эмпирических моментов, сколько требуется оценить неизвестных параметров распределения. Желательно применять моменты младших порядков, так как погрешности вычисления оценок резко возрастают с увеличением порядка момента;

· вычисленные по ЭД оценки моментов приравниваются к теоретическим моментам;

· параметры распределения определяются через моменты, и составляются уравнения, выражающие зависимость параметров от моментов, в результате получается система уравнений. Решение этой системы дает оценки параметров распределения генеральной совокупности.

Пример 2.4. Предположим, что случайная величина Х имеет гамма-распределение. Необходимо найти оценки параметров этого распределения (можно отметить, что нормальное распределение является частным случаем гамма-распределения).

Решение. Функция плотности гамма-распределения имеет вид

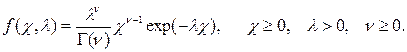
Распределение характеризуется двумя параметрами ν и λ, поэтому следует выразить один параметр через оценку математического ожидания, а другой – через оценку дисперсии. Математическое ожидание и дисперсия этого распределения равны ν/λ и ν/λ ² соответственно. Пусть их оценки определены равны:

α₁= 27,51, μ₂ = 0,91.

Составим систему уравнений для оцениваемых параметров

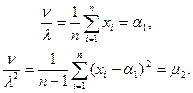
Разделив оценку математического ожидания на оценку дисперсии, получим

λ =α₁/μ₂ =30,12,

Метод моментов позволяет получить состоятельные, достаточные оценки, они при довольно общих условиях распределены асимптотически нормально. Смещение удается устранить введением поправок. Эффективность оценок невысокая, т.е. даже при больших объемах выборок дисперсия оценок относительно велика (за исключением нормального распределения, для которого метод моментов дает эффективные оценки). В реализации метод моментов проще метода максимального правдоподобия. Напомним, что метод целесообразно применять для оценки не более чем четырех параметров, так как точность выборочных моментов резко падает с увеличением их порядка.