ОЦЕНКИ МОМЕНТОВ И КВАНТИЛЕЙ РАСПРЕДЕЛЕНИЯ
Для характеристики эмпирического распределения можно использовать оценки центральных и начальных моментов. Применение находят моменты до четвертого порядка включительно, так как точность выборочных моментов резко падает с увеличением их порядка, в частности, дисперсия начальных моментов порядка r зависит от моментов порядка 2r. Она становится значительной для моментов высокого порядка даже при больших объемах выборки. Выборочные значения моментов определяют непосредственно по выборке или по сгруппированным данным.
Выборочные значения центральных моментов случайной величины X вычисляются по выборке с применением с формул
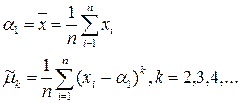 (2.1)
(2.1)
Указанные величины являются оценками соответствующих теоретических моментов распределения и должны рассматриваться как случайные. Вычисления по формулам (2.1) дают состоятельные, но смещенные оценки моментов старше первого. Смещение удается устранить введением поправочных коэффициентов, зависящих от объема выборки. Несмещенными и состоятельными будут оценки
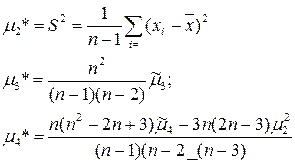 (2.2)
(2.2)
Оценки моментов по сгруппированным ЭД
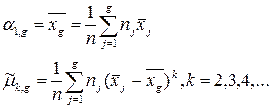 (2.3)
(2.3)
где 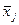 – центр j-го интервала; g – количество интервалов. Первый и последний интервалы могут быть открытыми. Тогда для них центры устанавливаются экспертным путем, исходя из сущности параметра.
– центр j-го интервала; g – количество интервалов. Первый и последний интервалы могут быть открытыми. Тогда для них центры устанавливаются экспертным путем, исходя из сущности параметра.
Группирование и приписывание соответствующей частости значения варианты в середине интервала группирования вносят некоторые искажения (при этом подразумевается, что распределение результатов наблюдения внутри интервала равномерное). Если распределение непрерывно и имеет достаточно высокий порядок соприкосновения с осью абсцисс (значения функции плотности распределения быстро убывают при удалении от центра распределения), то для снижения ошибок группирования используют поправки Шеппарда. Уточненные значения выборочных моментов для случая равной длины всех интервалов определяются через оценки моментов, вычисленные по сгруппированным данным:
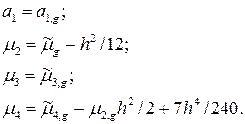 (2.4)
(2.4)
где h – длина интервала группирования. Указанные поправки ведут к уточнению только при соблюдении указанного условия, в противном случае они могут привести к еще большей ошибке.
Начальный эмпирический момент порядка r по несгруппированным данным определяется соотношением
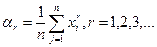 (2.5)
(2.5)
Центральные и начальные оценки моментов связаны между собой следующими зависимостями:
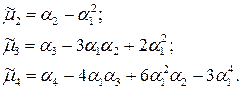 (2.6)
(2.6)
В процессе обработки ЭД проще сначала определить оценки начальных моментов, потом перейти к смещенным оценкам центральных моментов и затем вычислить несмещенные оценки.
Оценки моментов (в том числе среднее арифметическое) могут быть дробными величинами, даже если значения параметров являются целыми.
Квантилью, отвечающей уровню вероятности G, называют такое значение варианты xG, при котором функция распределения случайной величины принимает значение G, т. е. квантиль – это значение аргумента xG функции распределения, при котором F(xG)=G.
Эмпирическую квантиль находят по заданному значению вероятности G, используя вариационный ряд или ступенчатую ломаную линию.
Наряду с указанными параметрами для описания распределений применяются и другие характеристики:
· среднеквадратическое отклонение ;
· коэффициенты асимметрии и эксцесса ;
· стандартизованные переменные u=(x–α1)/S (S—средне квадратичное отклонение).
Стандартизация переменной позволяет упростить расчеты, кроме того, в литературе многие справочные статистические таблицы приводятся именно для стандартизованных переменных. Нетрудно показать, что математическое ожидание стандартизованной переменной равно нулю, а дисперсия равна единице, т.е. после такого преобразования ЭД справедливы следующие соотношения:
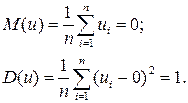
Величина u называется центрированной и нормированной. Переход от центрированной и нормированной величины к исходной осуществляется простым преобразованием x=uS+m1. Потери информации при стандартизации и обратном преобразовании не происходит.
Анализируя назначение рассмотренных параметров, необходимо отметить следующее. Одни параметры характеризует средние величины, а другие – вариацию. Главное назначение средних величин (оценок начальных моментов и в первую очередь первого момента распределения) состоит в их обобщающей функции. Это обобщение позволяет заменить множество различных индивидуальных значений показателя средней величиной, характеризующей всю однородную совокупность. Иначе говоря, средняя величина является типической характеристикой варианты в конкретной выборке. Иногда средняя величина обобщает и неоднородные совокупности данных. Например, может применяться такой показатель как среднее количество обработанных запросов на сервере в течение суток, хотя очевидно, что дневная загрузка сервера сильно отличается от загрузки в ночное время. Указанный показатель имеет смысл для оценки ресурса накопителей на жестких дисках. Наряду оценками математического ожидания (средними величинами в формулах 2.1 и 2.5) находят применение и другие оценки – среднее геометрическое, среднее гармоническое значение.
Каждый элемент ЭД формируется под влиянием как общих закономерностей, так и особых условий и случайных событий. Следовательно, в обработке ЭД большой интерес представляют вопросы оценки величин, характеризующих вариацию значений параметра у разных объектов или у одного и того же объекта в разные моменты времени. Вариацией какого-либо параметра (показателя) в совокупности наблюдений называется различие его значений у разных элементов этой совокупности.
Дата добавления: 2015-05-05; просмотров: 1889;
