ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ И ИХ СВОЙСТВА

Значение параметра, вычисленное по ограниченному объему ЭД, является случайной величиной, т. е. значение такой величины от выборки к выборке может меняться заранее не предвиденным образом. Следовательно, в результате обработки ЭД определяется не значение параметра Θ, а только лишь его приближенное значение – статистическая оценка параметра Θ*. Оценка есть неточное, неполное, приближенное отображение параметра. Получить статистическую оценку параметра теоретического распределения означает найти функцию от имеющихся результатов наблюдения, которая и даст приближенное значение искомого параметра. Различают два вида оценок – точечные и интервальные. Точечными называют такие оценки, которые характеризуются одним числом. При малых объемах выборки точечные оценки могут значительно отличаться от истинных значений параметров, поэтому их применяют при большом объеме выборки. Интервальные оценки задаются двумя числами, определяющими вероятный диапазон возможного значения параметра. Эти оценки применяются для малых и для больших выборок. Рассмотрим вначале точечные оценки.

Применительно к каждому оцениваемому параметру закона распределения генеральной совокупности существует множество функций, позволяющих вычислить искомые значения. Например, оценку математического ожидания можно вычислить, взяв среднее арифметическое выборочных значений, половину суммы крайних членов вариационного ряда, средний член выборки и т.д. Указанные функции отличаются качеством оценок и трудоемкостью реализации.

Качество оценок характеризуется такими свойствами, как состоятельность, несмещенность, эффективность и достаточность.

Состоятельность характеризует сходимость по вероятности оценки Θ* к истинному значению параметра Θ при неограниченном увеличении объема выборки n. Для состоятельности оценки достаточно, но не обязательно, чтобы математическое ожидание квадрата отклонения оценки от параметра M[Θ – Θ*]² стремилось к нулю с увеличением объема выборки (здесь и далее символ М означает математическое ожидание). Свойство состоятельности проявляется при неограниченном увеличении n, а при небольших объемах ЭД наличие этого свойства еще недостаточно для применения оценки.

Несмещенность характеризует отсутствие систематических (в среднем) отклонений оценки от параметра при любом конечном, в том числе и малом, объеме выборки, т. е.

M[Θ*] =Θ.

Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Не всегда наличие смещения плохо. Оно может быть существенно меньше погрешности регистрации значений параметра или давать дополнительную гарантию выполнения требований к значению параметра (если даже при положительном смещении оценка Θ*меньше предельно допустимого значения, то несмещенное значение тем более будет отвечать этому условию). В таких ситуациях допустимо применение смещенных оценок, если они вычисляются проще, чем несмещенные. Но даже несмещенная оценка может быть удалена от истинного значения.

Эффективность характеризует разброс случайных значений оценки около истинного значения параметра. Среди всех оценок следует выбрать ту, значения которой теснее сконцентрированы около оцениваемого параметра. Для многих применяемых способов оценивания выборочные распределения параметров асимптотически нормальны, поэтому часто мерой эффективности служит дисперсия оценки. В таком понимании эффективная оценка – это оценка с минимальной дисперсией. При неограниченном увеличении n эффективная оценка является и состоятельной. В случае оценивания одного параметра дисперсия несмещенной оценки отвечает условию Рао – Крамера

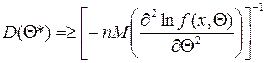
где f(x,Θ) – плотность распределения варианты; n – количество наблюдений.

Сравнительная эффективность оценки с дисперсией D_n[Θ*] измеряется коэффициентом эффективности

ε =D[Θ*]/D_k[Θ*],

который не превышает единицы. Чем ближе коэффициент ε к единице, тем эффективнее оценка. Отмеченное ограничение применимо и к дискретным распределениям, если вместо плотности распределения подставить в него функцию вероятности.

Достаточность характеризует полноту использования информации, содержащейся в выборке. Другими словами, оценка Θ* будет достаточной, если все другие независимые оценки на основе данной выборки не дают дополнительной информации об оцениваемом параметре. Эффективная оценка обязательно является и достаточной.

Рассмотренные свойства применимы также и к ЭД, которые характеризуются многомерными распределениями вероятностей.

Подходы к формированию оценок разработаны в теории несмещенных оценок, предложенной А. Н. Колмогоровым и С. Рао. В данной теории предполагается известным с точностью до параметра Θ вид функции плотности распределения наблюдаемой случайной величины f(x, Θ). Вид распределения устанавливается исходя из априорных соображений, например, на основе общепринятых суждений о характере безотказной работы технических средств. Тогда задача сводится к нахождению такой функции от результатов наблюдений, которая дает несмещенную и эффективную оценку.