ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
Методы обработки ЭД опираются на базовые понятия теории вероятностей и математической статистики. К их числу относятся понятия генеральной совокупности, выборки, эмпирической функции распределения.
Под генеральной совокупностью понимают все возможные значения параметра, которые могут быть зарегистрированы в ходе неограниченного по времени наблюдения за объектом. Такая совокупность состоит из бесконечного множества элементов. В результате наблюдения за объектом формируется ограниченная по объему совокупность значений параметра x1, x2, …, xn. С формальной точки зрения такие данные представляют собой выборку из генеральной совокупности. Наблюдаемые значения xi называют вариантами, а их количество – объемом выборки n. Для того чтобы по результатам наблюдения можно было делать какие-либо выводы, выборка должна быть репрезентативной (представительной), т. е. правильно представлять пропорции генеральной совокупности. Это требование выполняется, если объем выборки достаточно велик, а каждый элемент генеральной совокупности имеет одинаковую вероятность попасть в выборку.
Пусть в полученной выборке значение x1 параметра наблюдалось n1 раз, значение x2 – n2 раз, значение xk – nk раз, n1 + n2 + … + nk= n. Совокупность значений, записанных в порядке их возрастания, называют вариационным рядом, величины ni – частотами, а их отношения к объему выборки ni = ni / n – относительными частотами (частостями). Очевидно, что сумма относительных частот равна единице. Другой формой вариационного ряда является ряд накопленных частот, называемый кумулятивным рядом.
Под распределением понимают соответствие между наблюдаемыми вариантами и их частотами или частостями. Пусть nx – количество наблюдений, при которых случайные значения параметра Х меньше x. Частость события X<x равна nx / n. Это отношение является функцией от x и от объема выборки: Fn(x)= nx / n. Величина Fn(x) обладает всеми свойствами функции распределения:
· Fn(x) – неубывающая функция, ее значения принадлежат отрезку [0 – 1];
· если x1 – наименьшее значение параметра, а xk – наибольшее, то Fп(x)=0, когда x<=x1, и Fп(x)=1, когда x>xk .
Функция Fп(x) определяется по ЭД, поэтому ее называют эмпирической функцией распределения. В отличие от эмпирической функции Fn(x) функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения, она характеризует не частость, а вероятность события X<x. Из теоремы Бернулли вытекает, что частость Fn(x) стремится по вероятности к вероятности F(x) при неограниченном увеличении n. Следовательно, при большом объеме наблюдений теоретическую функцию распределения F(x) можно заменить эмпирической функцией Fn(x).
Основные свойства функции Fn ( x).
1. 0 Fn(x) 1.
2. Fn (x) - неубывающая ступенчатая функция.
3. Fn(x) = 0, x x1 .
4. Fn(x) = 1, x > xn .
Пример 2.1 Задана выборка случайной величины X: {4 3 3 5 2 4 3 4 4 5}. Построить график эмпирической функции распределения Fn(x).
Решение. Вариационный ряд случайной величины имеет вид {2 3 3 3 4 4 4 4 5 5}. Затем выделяем полуинтервалы (-,2], (2,3], (3,4], (4,5], (5,+]. На полуинтервале (-,2] Fn(x)=0/10=0. При 2<x3 Fn(x)=1/10=0,1.
Аналогично определяем значения Fn(x) на остальных полуинтервалах:
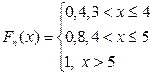 .
.
График функции Fn(x)приведен на рис. 2.1.

Замечание. В каждой точке оси x, соответствующим значениям xi функция Fn(x) имеет скачок. В точке разрыва Fn(x) непрерывна слева и принимает значение, выделенное знаком 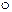 .
.
Дата добавления: 2015-05-05; просмотров: 1427;
