ФИЗИЧЕСКИЕ ОСНОВЫ ПОЛУЧЕНИЯ ИНФОРМАЦИИ

Вся объективная информация об окружающем нас мире, физические, химические и другие количественные теории, промышленное производство базируются на результатах измерений. Процессы во Вселенной и живой клетке, в центрах звезд и молекулах, в ракетном двигателе и атоме могут быть поняты в той мере, в какой удается создать их описание, называемое в науке «моделью». Что это означает? Это означает, что мы мысленно выделяем некий объект из его окружения (Солнце из совокупности звезд, клетку из их совокупности в организме и т.д.) путем описания его отличительных свойств.

При корректном описании свойств объектов можно понять, как их идентифицировать и чем они отличаются. Например, Солнце отличается от клетки размерами, температурой, спектром и мощностью электромагнитного излучения.

Сложность заключается в том, что на уровне одних рассуждений мы никуда не продвигаемся в понимании свойств объектов и только запутываем вопрос. Действительно, в рассматриваемом примере необходимо ответить на вопросы: что такое «размер», «температура», «спектр», «мощность» и т.д. Во-вторых, каким-то образом определить для каждого объекта характерные «размер», «температуру», «спектр», «мощность»; в-третьих, ввести градации свойств, с тем, чтобы можно было говорить о малости этого свойства в одном объекте по сравнению с другим.

Ответы на поставленные вопросы дает наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности, называемая метрологией. В метрологии рассматриваются вопросы получения и представления объективной количественной информации о физических объектах; источником ее являются результаты измерений.

Под физической величиной понимается некоторое свойство физических объектов, качественно общее для них, но в количественном отношении индивидуальное для каждого объекта [1]. Например, линейный размер является свойством космического объекта (звезды, галактики) и отдельного атома. То же самое относится к массе, температуре и другим свойствам физических объектов.

Необходимо подчеркнуть, что реальные объекты обладают бесконечным числом свойств. Выбирая некоторые из них для измерений, мы мысленно упрощаем физический объект, создаем его модель той или иной степени сложности. Это обстоятельство необходимо всегда иметь в виду, поскольку грубые модели, во-первых, могут существенно исказить представления о физическом объекте и, во-вторых, увеличить погрешности результатов измерений. Например, определяется величина электрического тока в цепи по показаниям амперметра, измеряющего действующее значение тока. Если форма реального тока в цепи отлична от синусоиды, то показания амперметра (пренебрегая его собственной погрешностью) будут содержать ошибку тем большую, чем больше реальная форма тока отличается от синусоиды. Если форма тока приближается к прямоугольной, то погрешность может составить десятки процентов.

В предыдущем абзаце содержится логическое противоречие: чтобы измерить физическую величину какого-либо объекта необходимо построить его модель, а для построения модели необходимо сначала выполнить измерения для определения параметров модели. Указанное противоречие является объективно существующим фактором процесса познания. Преодолевается оно методом последовательных приближений: сначала строится грубая модель объекта и проводятся измерения его параметров; по мере получения результатов измерений модель уточняется, и вновь проводятся измерения, но уже более точные и т. д.

Так что же понимается под термином «измерение»? Под измерением понимается нахождение значения физической величины путем физического эксперимента сравнения данной физической величины с известной физической величиной того же рода, принятой за единицу измерения.

Чтобы величина была измерима, она должна обладать свойствами аддитивности, т.е. для нее должно быть известно как физически (а не математически) выполнить операции сравнения и сложения (суммирования).

Рассмотрим следующий пример. Имеется стержень длиной X. Возьмем второй стержень и совместим один его конец с концом первого стержня, а выступающую за противоположный конец первого стержня часть второго стержня удалим (отрежем). Мы выполнили операцию сравнения. Получились два стержня длинной X. Расположив их один за другим по одной прямой соприкасающимися концами, получим общую длину X₁ = X + X = 2 X, тем самым, выполнив операцию физического суммирования. Продолжая указанный процесс, можно сопоставить стержень длиной X со стержнем любой другой длины nּX, где n - целое число (более подробный анализ процедур сравнения и что делать, если n не целое число, выходит за рамки данного курса и описан в учебниках по метрологии). Теперь достаточно принять длину X за единицу измерения 1_X, чтобы реализовать основное уравнение измерений

X _n = n ·1_X,

где 1_X – принятая за единицу величина той же природы, что и X_n; имеет соответствующее наименование (один метр, один фут, один дюйм);

n - неименованное число, указывающее сколько единиц измерения 1_X содержит измеряемая физическая величина X_n; называется это число числовым значением величины.

Следовательно, физическая величина «длина» является аддитивной и ей может быть сопоставлено число, указывающее во сколько раз данная физическая величина X_n больше такой же по природе физической величины, принятой за единицу измерения 1_X. Свойством аддитивности обладают такие физические величины, как длина, площадь, масса, время, электрический ток и другие. Их называют экстенсивными (аддитивными) величинами.

Приведенное основное уравнение измерений, будучи чрезвычайно простым в записи, довольно сложно реализуется в виде технических устройств.

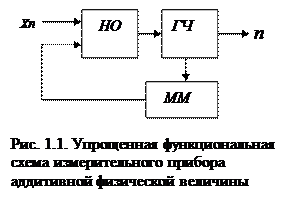
Во-первых, необходимо иметь набор единиц физической величины и устройство их суммирования (набор гирь, устанавливаемых на чашку весов; набор единичных отметок длины на линейке; набор электрических сопротивлений и т.д.). Средство измерений, хранящее в приборе единицу физической величины 1_X, называется мерой. Чтобы сравнивать с мерой входную величину, согласно уравнению, количество мер должно быть равно максимальному значению n. Такое устройство называется магазином мер (ММ).

Во-вторых, нужно устройство, которое обеспечивало бы выполнение операции сравнения измеряемой физической величины X_n с установленным на магазине значением n ·1_X. Такое устройство называется нуль – органом (НО) или компаратором. На выходе НО появляется один из трех сигналов: X_n больше n ·1_X; X _n меньше n ·1_X; X _n= n ·1_X.

В третьих, должно быть устройство выработки и хранения чисел n. По сигналу с НО числа n должны возрастать (если X_n > n ·1_X), уменьшаться (если X_n < n·1_X). Назовем это устройство генератором чисел (ГЧ). По сигналу с ГЧ в магазине мер количество единиц должно возрастать или уменьшаться согласно росту или уменьшению числа n. Процесс измерения считается завершенным в тот момент, когда на выходе НО появляется сигнал равенства X_n = n ·1_X. Установившееся в ГЧ число n будет числовым результатом измерения физической величины X _n.

Описанный процесс измерений можно представить следующей упрощенной функциональной схемой (рис. 1.1).

Теперь попытаемся указанным выше способом организовать измерение температуры. Выясняется, что нет процедур, позволяющих непосредственно установить температуру тела А равной температуре тела В, можно только дать оценку у какого из тел температура выше. Как реализовать операцию суммирования температур тел А и В вообще неясно. Например, имеется два ведра с водой какой – то температуры. Сольем воду в одну бочку. Понятно, что при этом объем воды в бочке станет равен сумме объемов ее в каждом ведре (объем – аддитивная величина). А температура? Тоже сложится? Очевидно, нет. Например, если температура воды в ведрах была одинакова, то после объединения в бочке она останется такой же.

Подобные физические величины, не обладающие свойством аддитивности, называются интенсивными (неаддитивными). В рамках данного выше определения измерений и их основного уравнения такие величины не могут быть измеримыми. В то же время, интенсивные величины (температура, плотность, давление, твердость) являются определяющими параметрами физических и химических процессов и без знания их значений невозможен ни теоретический анализ, ни техническая реализация большинства физических и химических процессов.

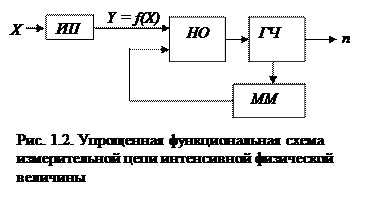
Выход из тупика был найден Г. Галилеем (1564-1642 г.г.) и заключается он в следующем. Для подлежащей определению интенсивной физической величины Х ищут экстенсивную величину Y, связанную хорошо изученной зависимостью Y = f(X) с интенсивной величиной. Измеряют экстенсивную величину Y и по известной зависимости X = f ^-1(Y) определяют значение интенсивной физической величины X. Так, давление с помощью мембраны или сильфона преобразуется в линейное перемещение, измерять которое мы умеем. Температура может быть преобразована в линейное перемещение жидкости в трубке, угловое перемещение биметаллической пластинки, приращение омического сопротивления проводника или полупроводника и т.д. Таким образом, в процедуры измерения вошла операция преобразования одной физической величины в другую.

Экстенсивные величины, как выясняется при более подробном рассмотрении, в большинстве случаев так же не могут быть непосредственно сопоставлены с единицей соответствующей физической величины. Измерения расстояний до космических объектов, измерения электрических и магнитных величин (тока, напряжения, мощности, индуктивности и т.д.) могут быть выполнены только с помощью преобразования измеряемой величины в связанную с ней функциональной зависимостью другую, легко измеримую физическую величину. Таким образом, мы приходим к понятию «измерительный преобразователь», т.е. устройству, преобразующему одну физическую величину в другую по известной функциональной зависимости.

Не всякий преобразователь может быть отнесен к категории «измерительный». Например, обычный рычаг является преобразователем силы, но его нельзя считать «измерительным преобразователем». Чтобы преобразователь отнести к категории «измерительный», он должен обладать набором характеристик, позволяющих определить степень отличия преобразованной величины данным преобразователем от преобразованной величины, полученной с помощью некоего «идеального» преобразователя. Указанные характеристики называются метрологическими характеристиками и в дальнейшем будут рассмотрены более подробно. Теперь можно дать точное определение термину «измерительный преобразователь».

Измерительный преобразователь (ИП) – техническое средство, имеющее метрологические характеристики, предназначенное для преобразования измеряемой величины в другую величину или измерительный сигнал, удобный для обработки, хранения, дальнейших преобразований, индикации или передачи [1].

Функциональная схема измерительной цепи интенсивной физической величины, в которую входит ИП, представлена на рис. 1.2.

В процессе развития измерительной техники измерительные преобразователи получили широчайшее распространение для преобразования не только интенсивных, но и экстенсивных физических величин и входят в состав измерительных приборов и систем в качестве важнейших устройств.

Отметим два существенных обстоятельства, связанных с ИП.

Первое. Преобразование физической величины в измерительный сигнал, пригодный для сравнения с мерой, достигается, чаще всего, рядом преобразований. Например, изменение температуры преобразуется в изменение величины электрического сопротивления проволоки; сопротивление преобразуется в напряжение; напряжение усиливается (что тоже есть измерительное преобразование) и только после этого подается на НО для сравнения с мерой. Поэтому под ИП на рис. 1.2 нужно понимать, в общем случае, последовательность ИП. Первый конструктивно обособленный ИП называется датчиком.

Второе. Преобразование одной и той же физической величины может выполняться ИП, работающими на различных принципах измерений (принцип измерений – физическое явление или эффект, положенное в основу преобразований [1]). Например, изменение температуры можно преобразовать в линейное перемещение столба жидкости (как в медицинском термометре), в изменение электрического сопротивления или электрического напряжения. Объемный расход жидкости можно преобразовать в частоту электрического сигнала, высоту подъема образцового тела специальной формы, величину электрического тока.

Практически все датчики преобразуют входные физические величины в тот или иной параметр электрического сигнала (амплитуду напряжения или тока, частоту или фазу синусоподобного сигнала и т.д.). Это связано с хорошо развитой техникой преобразования электрических сигналов, передачей их на большие расстояния, сравнения с мерой и получения кодов числовых значений величин. А коды легко вводятся в системы автоматического управления (регулирования) производственными процессами или выводятся на цифровые дисплеи для представления измерительной информации потребителю.

В данном пособии будет рассматриваться только та часть измерительных преобразований физических величин, которая связана с датчиками. Теория и технические реализации измерительных преобразователей, следующих за датчиками до получения результатов измерений, будут излагаться в других дисциплинах.

Обсуждение особенностей преобразования той или иной физической величины с целью получения измерительного сигнала, чем мы в дальнейшем и займемся, необходимо предварить кратким анализом общих для всех преобразователей свойств. Цель этого анализа – введение показателей, по которым одни физические эффекты будут считаться более предпочтительными, чем другие при преобразовании одних и тех же физических величин.