ВЕЩЕСТВО И ФИЗИЧЕСКИЕ ПОЛЯ
4.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Во введении было дано определение физической величины как «некоторое свойство физических объектов, качественно общее для них, но в количественном отношении индивидуальное для каждого объекта». Это определение, являясь обобщенным понятием, не дает понимания конкретных свойств физических объектов, подлежащих измерению. С другой стороны, сами средства измерений и, в частности, измерительные преобразователи, являются физическими объектами. Как же обеспечивается взаимодействие одних физических объектов (чьи свойства подлежат измерению), с другими, являющимися средствами измерений?
Из п. 2.7 ясно, что с энергетической точки зрения, измерительное преобразование сводится к переводу энергии одного вида в энергию другого (например, механической в электрическую) использованием известных физических явлений или эффектов. Поскольку физические объекты могут находиться в разных состояниях, то измерительные преобразования могут выполняться путем взаимодействий нескольких видов: вещества с веществом, поля с полем или поля с веществом.
Сначала дадим определение вещества и физического поля.
Под веществом понимаются физические объекты, обладающие массой в состоянии покоя.
Под физическим полем понимается особое состояние пространства вокруг вещества, проявляющееся в создании силового воздействия на частицы другого вещества, помещенного в любую точку этого пространства.
Строго говоря, данные выше определения не совсем точны. Дело в том, что поля при взаимодействии с веществом (фотоэффект, комптоновское рассеяние) проявляют себя как частицы, а электроны при прохождении через кристаллы рассеиваются как волны поля. Поэтому более точная модель материи соответствует единству вещества и поля, или, в терминах физики, материя обладает корпускулярно - волновым дуализмом. Указанные обстоятельства приходится учитывать при исследованиях свойств полупроводников, поверхностных явлений на границах сред и т.д.
Однако, для большей части задач технических измерений модель материи, при которой вещество и поле разделено, вполне приемлема. На нее и будем опираться.
4.2. ВЕЩЕСТВО
Любое вещество состоит на микроскопическом уровне из одних и тех же частиц – нейтронов, протонов и электронов, которые образуют атомы и молекулы. Но количество частиц в атомах и молекулах, их взаимное расположение и связи определяют различное макроскопическое (т.е. в больших объемах или масштабах) состояние вещества – в виде газа, жидкости, твердого тела или плазмы.
4.2.1. Газ – состояние вещества, в котором его частицы (молекулы или атомы) не связаны силами взаимодействия и движутся свободно, заполняя весь представленный им объем. Данное определение соответствует модели идеального газа.
Молекулы в газе при давлении 1,01·105 Па (1ат) и температуре 273,16 К (00С) расположены в среднем на расстоянии 1·10-8 м друг от друга, а силы межмолекулярного взаимодействия несущественны уже на расстояниях (0,5-1)·10-9 м. Это позволяет предполагать, что молекулы движутся хаотично и независимо друг от друга, соударяясь и разлетаясь как механические шары. При более низких давлениях расстояния между молекулами газа еще больше возрастают и его свойства с высокой точностью можно описать моделью идеального газа.
При сделанных предположениях, кинетическая теория газов дает уравнение связи между средней кинетической энергией одной молекулы и температурой газа в виде
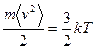 , (4.1)
, (4.1)
где m - масса одной молекулы;
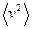 - средний квадрат скорости молекул;
- средний квадрат скорости молекул;
k = 1,38·10-23 Дж/К – константа, называемая постоянной Больцмана;
T – абсолютная температура.
Молекулы газа в своем хаотическом движении соударяются со стенками сосуда или мембраной датчика давления, передавая им часть своего импульса. В единицу времени на единицу площади стенки или мембраны передается импульс p, равный
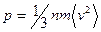 , (4.2)
, (4.2)
где n - количество молекул в единице объема.
Выражая в (4.2) произведение массы молекулы на среднюю скорость из (4.1), получим значение импульса, макроскопически воспринимаемого как сила, действующая на единицу площади (т.е. давление):
P = nkT.
Удобно рассматривать количество газа, равное массе одного моля, поскольку в этом случае количество молекул постоянно для любого газа и равно числу Авогадро N = 6,022·1023 моль-1. Для этого случая последнее выражение переходит в уравнение Клапейрона:
PV = RT, (4.3)
в котором R = Nk = 8,314 Дж/(моль·К) – универсальная газовая постоянная;
V – объем газа приходящийся на 1 моль при давлении Р.
Для произвольной массы газа m уравнение (4.3) записывается в виде уравнения Менделеева – Клапейрона:
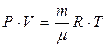 . (4.4)
. (4.4)
где µ - масса одного моля газа.
Часто в расчетах используется плотность газа ρ, равная массе газа в единице объема:
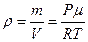 . (4.5)
. (4.5)
С ростом давления молекулы газа сближаются, их взаимодействие становится значительным и уравнение связи параметров газа (при давлениях выше 1 МПа) существенно усложняется по сравнению с (4.3).
Если газ охлаждать, то его плотность растет и при определенной температуре происходит конденсация газа, т.е. его переход в жидкое состояние.
Можно поступить по-другому: при постоянной температуре повышать давление до получения жидкой фазы. Однако для каждого газа есть критическая температура ТКР, выше которой газ не переходит в жидкое состояние ни при каких давлениях. Минимальное давление, при котором газ еще переходит в жидкое состояние при критической температуре ТКР, называется критическим давлением РКР. Газ с температурой ниже ТКР называется паром.
В таблице 4.1 приведены параметры критической точки и объем vКР одного килограмма газа в этой точке для ряда распространенных газов.
Таблица 4.1
Параметры критической точки некоторых газов
|
4.2.2. Жидкость – агрегатное состояние вещества, промежуточное между твердым и газообразным. Как твердое тело, жидкость сохраняет свой объем, образует поверхность; как газ - принимает форму сосуда, в котором находится. Отличительная особенность жидкости – текучесть.
Качественно текучесть объясняется наличием в жидкости объединений молекул, в которых тепловые движения происходят упорядочено. Отдельные молекулы, за счет избыточной тепловой энергии, рвут связи в своем объединении и переходят в соседнее. Средняя частота таких скачков составляет 1011 - 1012 с-1. При наличии внешней силы большая часть скачков молекул происходит по направлению силы, что макроскопически проявляется как текучесть.
4.2.3. Твердое тело - агрегатное состояние вещества, характеризующееся стабильностью формы. Атомы (или молекулы) твердых веществ удерживаются на среднем расстоянии друг от друга порядка 1·10-10 м, на котором уравновешиваются электростатические силы отталкивания и притяжения.
Частицы многих твердых тел образуют на микроскопическом уровне периодическую пространственную структуру – кристаллическую решетку. В узлах кристаллической решетки могут находиться атомы, молекулы или ионы, совершающие вращательные движения и малые колебания вокруг положений равновесия.
С точки зрения протекания электрического тока тела делятся на диэлектрики (удельное сопротивление 1012-1014 Ом·м), металлы (удельное сопротивление 10-2-10-4 Ом·м) и полупроводники, у которых сопротивление меньше, чем у диэлектриков, но которое, в отличие от металлов, понижается с ростом температуры. Чтобы понять в общих чертах свойства твердых тел, необходимо предварительно рассмотреть электрические поля, которые и определяют макроскопические свойства твердых тел.
4.3. ОПИСАНИЕ ФИЗИЧЕСКИХ ПОЛЕЙ
Как было указано выше, под физическим полем понимается особое состояние пространства вокруг вещества, проявляющееся в создании силового воздействия на качественно подобное вещество, в любой точке этого пространства.
В соответствии с данным определением можно говорить о поле скоростей движущегося газа (например, ветра на разных высотах), поле температур (при передаче тепла от какого-либо объекта), поле электрических или магнитных сил, поле притяжения материальных тел независимо от их природы (поле тяготения).
Физические поля существуют в трехмерном пространстве и изменяются во времени. Следовательно, их описание должно даваться функцией (или функциями) от трех координат (в декартовой системе) и времени. Анализ подобных выражений оказывается крайне сложным. Поэтому, по возможности, выражения упрощают, рассматривая различные частные случаи.
С точки зрения зависимости от времени, поля разделяют на статические, не зависящие от времени; стационарные, параметры которых изменяются во времени периодически по известным зависимостям и нестационарные, изменяющиеся во времени без периодического повторения значений поля в отдельных точках пространства. Проще всего рассматривать статические и стационарные поля, и мы начнем рассмотрение именно с них.
С точки зрения пространственного воздействия на физические объекты, поля делятся на скалярные и векторные.
Скалярное поле - это поле, параметр которого в каждой точке пространства задается одним числом. Например, распределение (поле) температуры металлического бруска, нагреваемого с одного конца. В каждой точке бруска температура своя, но ее значение зависит только от координаты рассматриваемой точки и времени нагрева t, и не зависит от какого – то выделенного направления. Поэтому, выбрав некоторую систему координат, температуру Т в любой точке бруска можно представить как функцию координат (x,y,z) и времени t: Т = f(x,y,z,t).
Предположим, скалярное поле статично, т.е. значения температур в каждой точке бруска остаются неизменными во времени. Тогда можно соединить мысленно все точки равной температуры, они образуют поверхность равных температур. В каждой точке указанной поверхности можно указать направление, по которому температура нарастает быстрее всего. Еще раз подчеркнем, что речь идет не о повышении температуры во времени, а о росте (или спаде) ее в пространстве, при переходе от точки к точке. Указанное направление быстрейшего роста или спада скалярного поля называется градиентом (в уравнениях пишут или grad T или используют специальный знак ΔT).
Градиент, как характеристика скорости пространственного нарастания поля, включает в себя производные по координатам, а как характеристика направления - является вектором. Окончательно – градиент функции T(x,y,z) есть вектор, проекциями которого на координатные оси служат значения частных производных этой функции.
В литературе принято обозначать направления координатных осей x, y, z единичными векторами, т.е. стрелками, направленными по соответствующим координатным осям и длиной в одну единицу; эти единичные вектора обозначаются соответственно буквами i, j, k (вектора будут обозначаться жирными буквами). В указанных стандартных обозначениях градиент температурного поля запишется так:
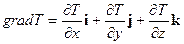 . (4.8)
. (4.8)
Предполагается, что читатель знаком с элементарными операциями над векторами, в частности, что сумма векторов есть вектор, полученный по правилу параллелограмма, а разность двух векторов есть вектор, направленный от конца одного к концу другого.
Векторное поле – это поле, параметр воздействия на физические объекты которого в каждой точке пространства задается величиной и направлением действия. Для описания векторного поля используют два метода:
- графический, когда значение поля в каждой точке пространства изображают в виде стрелки (вектора), направление которой показывает направление действия поля в данной точке, а длина в условных единицах равна величине (модулю) поля в этой точке;
- аналитический, в котором вектор обозначается либо в виде выделенной жирным шрифтом буквы (например, сила F), либо в виде буквы, умноженной на вектор единичной длины. Например, выражение для импульса частицы: p = mּνּn, где p – вектор импульса; m – масса частицы; v – модуль скорости частицы; n – единичный вектор скорости, т.е. вектор, модуль которого равен единице, а направление совпадает с направлением скорости частицы.
 Для полного уяснения правил изображения векторных полей и выполнения некоторых математических операций с векторами, рассмотрим точки на поверхности диска, вращающегося с постоянной угловой скоростью (см. рис. 4.1).
Для полного уяснения правил изображения векторных полей и выполнения некоторых математических операций с векторами, рассмотрим точки на поверхности диска, вращающегося с постоянной угловой скоростью (см. рис. 4.1).
Выделим на поверхности диска некую точку А и проведем к ней из центра круга О радиус – вектор r, который не только определяет минимальное расстояние от центра О до точки А, но и указывает в системе координат, связанной с диском, направление на точку А. Ясно, что r – вектор (имеет длину и определенное направление).
Относительно системы координат, не связанной с диском, видно, что радиус – вектор r вращается с постоянной периодичностью вокруг точки О, образуя стационарное векторное поле. Другими словами: все точки на радиусе – векторе r, описав угол 2π за время Δt, возвращаются в исходное состояние; интервал времени Δt называется периодом вращения.
Угол, на который поворачивается за единицу времени вектор r, называется угловой скоростью вращения ω. Отношение угла к интервалу времени ω = 2π/Δt является, конечно, скаляром, но необходимо каким – то образом указать, что вращение происходит не хаотично в трехмерном пространстве, а в определенной плоскости (в нашем случае – это плоская поверхность диска).
Плоскость, согласно аналитической геометрии, задается перпендикуляром единичной длины к ней, который обозначен на рис. 4.1 буквой n. Окончательно имеем: все точки диска, вращающегося с постоянным периодом Δt, образуют поле постоянной угловой скорости ω = ωּn, причем, по договоренности, вектор ω направлен так, чтобы, глядя с его конца на диск, видно было перемещение радиуса – вектора r против движения часовой стрелки.
Каждая точка диска, кроме угловой скорости ω, имеет и линейную скорость v, которую легко вычислить: за время одного периода Δt точка на диске проходит путь 2πr, следовательно, v = 2πr/Δt. Поскольку ω = 2π/Δt, линейную скорость можно записать через угловую:
v= ω·r. (4.9)
Но диск вращается, точка А на нем непрерывно меняет свое положение, поэтому возникает вопрос: а куда же направлен вектор скорости? Он направлен, как легко доказать, по касательной к окружности. Сама касательная перпендикулярна радиусу r в точке касания и лежит в плоскости диска, то есть, перпендикулярна вектору угловой скорости ω.
Если вектор (в частности, скорости v) перпендикулярен плоскости, в которой лежат два других вектора (ω и r), то знаком × (векторное умножение) обозначают операцию получения вектора, перпендикулярного плоскости, в которой лежат перемножаемые вектора, а модуль нового вектора равен произведению модулей исходных векторов, умноженного на синус угла между ними. В рассматриваемом случае можно, следовательно, записать вектор линейной скорости, с учетом выражения (4.9), в виде
v = ω × r. (4.10)
Если вспомнить, что точки на радиусе – векторе имеют различные модули (т.е. расстояния от оси вращения), то можно заключить: на вращающемся диске точки образуют поле линейных скоростей, направленных по касательной к окружности вращения в каждой точке и величиной (модулем), пропорциональной расстоянию от центра вращения до соответствующей точки.
Непрерывное изменение направления линейной скорости v вращающейся точки А приводит к появлению центростремительного ускорения а, равного по модулю а = v2/r и направленного по радиусу – вектору r. По второму закону Ньютона, произведение массы материальной точки m на ускорение (вектор) создает силу, направленную по направлению ускорения. На рис. 4.1 в формуле силы задание направления достигается умножением произведения массы m и модуля ускорения v2/r на вектор r. Но вектор r может быть любой длины, поэтому умножение на него не только указывает направление действия силы, но изменяет и ее модуль. Чтобы указать направление силы F и исключить влияние длины вектора r, одновременно с умножением на него выражение делится на длину (модуль) вектора r, что дает в итоге
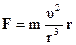 . (4.11)
. (4.11)
Мы рассмотрели поле скоростей и сил неподвижных материальных точек на вращающемся диске. А что будет, если по поверхности вращающегося диска материальная точка массой m движется с постоянной линейной скоростью vр вдоль радиуса – вектора r? Как показано в курсах теоретической механики, в этом случае на точку действует сила, лежащая в плоскости вращения (т.е. перпендикулярная вектору угловой скорости ω) и перпендикулярная вектору vр. Сила эта по имени описавшего ее ученого называется кориолисовой силой Fk и в векторной форме она равна:
Fk = 2 m vр × ω. (4.12)
Векторные поля можно, конечно, описать с помощью введения трехмерной системы координат, как это сделано для скалярного поля. Однако, подобное представление не слишком удобно: во–первых, результаты вычислений оказываются зависимыми от выбранных направлений осей координат; во–вторых, одному векторному уравнению соответствует три уравнения разложения вектора по координатным осям, что усложняет решение задач.
Поэтому обычно задача формулируется в векторной форме, далее переходят к разложению векторов по координатным осям, но при этом направления осей подбирают так, чтобы задача имела простое решение (например, одну из осей направляют по неизменному направлению поля), а окончательный результат решения вновь обобщают в векторной форме.
4.4. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
Электрическое поле, наряду с гравитационным и магнитным полями, наиболее часто встречающееся силовое поле. Указанные универсальные поля определяют взаимодействие частиц как внутри вещества на микроскопическом уровне (между ядрами атомов и электронами, между атомами и молекулами), так и на уровне макроскопическом, определяя все многообразие электромагнитных и гравитационных явлений. В измерительной технике гравитационное поле не имеет сколь ни будь существенного значения, и мы его отдельно рассматривать не будем.
Источником электрического поля являются элементарные заряды электрона и протона. Заряды эти равны между собой (1,60219ּ10-19 Кл) и противоположны по знаку в том смысле, что электрон от электрона отталкивается (и протон от протона), а электрон к протону притягивается. Условно заряд электрона назван отрицательным, а протона положительным.
Природа электрических зарядов не ясна, но известно, что:
- электрическая сила отталкивания между двумя электронами в 1040 больше их гравитационного притяжения. Именно поэтому строение веществ, их химические, механические, тепловые и другие макроскопические свойства определяются электрическими силами;
- величина заряда частиц остается постоянной при любой скорости их движения. Уникальное свойство, поскольку, согласно теории относительности, тела, в зависимости от относительной скорости движения, меняют геометрические размеры, массу и другие физические параметры.
В 1785 г. Шарль Кулон открыл основной закон взаимодействия электрических зарядов, названный его именем: если имеются две группы точечных зарядов q1 и q2, то сила взаимодействия между ними F в вакууме определяется выражением
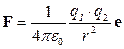 . (4.13)
. (4.13)
где e – единичный вектор направления от заряда q2 к q1;
r – расстояние между зарядами;
ε0 – константа, называемая электрической постоянной; по сути – это постоянный коэффициент, определяемый выбором системы единиц; в системе СИ константа равна 8,85·10-12 Ф/м.
Довольно часто закон (4.13) пишут в скалярной форме, словесно дополняя (или предполагая по умолчанию), что речь идет о выделенном направлении – прямой между зарядами. В этом случае единичный вектор e из выражения (4.13) исчезает. Такая запись неудачна. Это видно, если задать основной вопрос электростатики: как две (или больше) группы разнесенных в пространстве зарядов q1 и q2 воздействуют на третий заряд q3? Найти ответ без векторного представления направлений и сил не удастся.
Сформулированную задачу можно решать непосредственно, используя (4.13), но в этом случае любая замена величины или положения в пространстве заряда q3 потребует полного повторения всех выкладок.
Поэтому поступают следующим образом: рассматривают воздействие некоторой группы зарядов q1, помещенной в точку пространства с нулевыми координатами, на единичный заряд q2, помещенный в точку 1 пространства. Сила взаимодействия зарядов F(1) определится по закону Кулона. Можно сказать по-другому: сила F(1) описывает нечто (названное электрическим полем), существующее в точке 1 и при отсутствии в ней единичного заряда q2, а при помещении такого заряда – проявляющее себя как сила. Такое представление позволяет описать поле зарядов q1 без привлечения второго заряда q2. Для этого выражение (4.13) нужно поделить на q2. Полученная величина называется напряженностью электрического поля E(1) и она характеризует действие всех зарядов, кроме q2 в точке пространства, обозначенной цифрой 1. Размерность напряженности – В/м. Теперь получить значение силы, действующей на любой заряд в точке 1, не представляет трудности – для этого достаточно напряженность поля в точке 1, умножить на величину заряда, например q3, помещенного в эту точку,
F(1) = E(1)· q3. (4.14)
Введение понятия напряженности поля имеет глубокий смысл, поскольку позволяет разделить задачи расчета поля и расчета количества зарядов, вносимых в его отдельные точки.
Если заряды распределены в пространстве, то их напряженность E(1) в точке 1 определяется векторным суммированием напряженностей от отдельных групп зарядов:
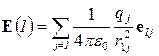 , (4.15)
, (4.15)
где qj – заряд j – той группы;
r1j – расстояние от точки 1 до j – той группы зарядов;
e1j – единичный вектор от точки 1 по направлению зарядов j – той группы.
 Теперь предположим, что в поле зарядов E перемещается малый заряд q1 из точки a в точку b. При этом, как известно из механики, совершается работа, равная скалярному произведению вектора силы на вектор перемещения вдоль траектории движения (рис. 4.2).
Теперь предположим, что в поле зарядов E перемещается малый заряд q1 из точки a в точку b. При этом, как известно из механики, совершается работа, равная скалярному произведению вектора силы на вектор перемещения вдоль траектории движения (рис. 4.2).
| |
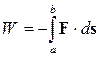 ,
,
или при перемещении единичного заряда
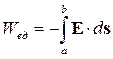 . (4.16)
. (4.16)
Допустим, перемещение единичного заряда из a в b шло по верхней траектории, а обратно – по нижней. Чему будет равна полная работа? Поскольку прямое перемещение выполнялось против сил поля, то обратное – по направлению сил и работа имеет знак плюс; сумма работ переноса заряда от a до b и обратно равна нулю. Если бы сумма работ по замкнутому контуру не была равна нулю, то выбирая соответствующим образом пути перемещения из точки a в b и обратно, мы получали бы работу без затраты энергии, т.е. вечный двигатель. Равенство нулю интеграла (4.16) по замкнутому контуру означает, что величина работы зависит только от разности потенциальных энергий точек a и b, называемой напряжением U и не зависит от формы пути:

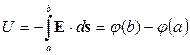 , (4.17)
, (4.17)
где φ(a) – потенциальная энергия единичного заряда после совершения работы по переносу его из бесконечности (где напряженность поля равна нулю) в точку a;
φ(b) - потенциальная энергия единичного заряда после совершения работы по переносу его из бесконечности в точку b.
Вычисляется потенциал любой точки поля достаточно легко. Например, для вычисления потенциала точки b необходимо в интеграле (4.17) нижний предел заменить бесконечностью, а путь, по которому заряд q переносится из бесконечности считать прямой линией (работа ведь не зависит от траектории переноса заряда). Получим:

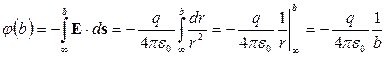 .
.
Потенциал от действия j групп зарядов qj в контролируемой точке 1 будет равен
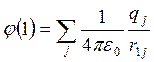 , (4.18)
, (4.18)
где r1j - расстояние от точки 1 до j – той группы зарядов.
Последнее выражение позволяет сделать два важных вывода:
- Для расчета работы, выполняемой зарядами в электрических полях достаточно вычислить скалярное поле потенциалов, что существенно легче, чем трехмерные вектора, описывающие напряженность поля.
- Электрические поля обладают свойством суперпозиции, т.е. поле каждой группы зарядов (или их потенциалы) действуют независимо от действия других зарядов (потенциалов), а суммарный эффект есть сумма действия отдельных потенциалов.
На этих свойствах базируются все расчеты линейных электрических цепей. Например, на какой-то элемент (для определенности - катушку с металлическим проводом, называемую индуктивностью) действует переменное и постоянное электрические поля. Суммарное движение зарядов в проводе катушки, называемое током, рассчитывают в два этапа: на первом этапе вычисляют отдельно движение зарядов от постоянного поля, отдельно от переменного, а на втором этапе - суммируют результаты расчетов.
Для перехода от скалярного поля потенциалов к векторному полю напряженностей, достаточно продифференцировать выражение (4.17). В итоге получится: E = - grad φ.
 В заключение рассмотрим практически важную систему двух разнесенных равных по величине, но разноименных, точечных зарядов +q и –q, называемую диполем. Примем, что расстояние между зарядами считается от отрицательного к положительному, т.е. расстояние l – вектор, длиной l. Как пример подобной системы можно указать на полярные молекулы, например, молекулу воды Н2О. В ней атомы водорода расположены не симметрично относительно атома кислорода, а под углом в 1050. Поэтому суммарный отрицательный заряд иона кислорода несколько смещен относительно суммарного положительного заряда ионов водорода и образуется диполь.
В заключение рассмотрим практически важную систему двух разнесенных равных по величине, но разноименных, точечных зарядов +q и –q, называемую диполем. Примем, что расстояние между зарядами считается от отрицательного к положительному, т.е. расстояние l – вектор, длиной l. Как пример подобной системы можно указать на полярные молекулы, например, молекулу воды Н2О. В ней атомы водорода расположены не симметрично относительно атома кислорода, а под углом в 1050. Поэтому суммарный отрицательный заряд иона кислорода несколько смещен относительно суммарного положительного заряда ионов водорода и образуется диполь.
Рассмотрим потенциал поля, образуемый диполем на большом расстоянии от самих зарядов. «Большое расстояние» означает, что расстояние между зарядами l пренебрежимо мало по сравнению с расстоянием до точки, в которой определяется потенциал системы.
На рис.4.3 изображен диполь, у которого начало координат помещено в точку О, удаленную от обоих зарядов на l/2 и точка в пространстве N, удаленная на расстояние r от начала координат, в которой необходимо вычислить величину поля от действия зарядов диполя.
Обозначим расстояние от зарядов –q
|
|
|
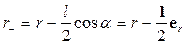
(4.19)
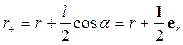 .
.
В выражениях учтено, что длина диполя l, умноженная на cosα является проекцией вектора l на направление единичного вектора er, т.е. скалярным произведением указанных векторов.
Потенциал в точке N, согласно (4.18) равен
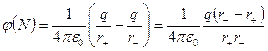 .
.
Произведение в знаменателе r+ r- можно приближенно заменить r2, а разность длин в числителе, с учетом (4.19), равна l·er. Следовательно
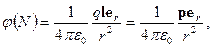 (4.20)
(4.20)
где p = q·l – вектор, называемый электрическим моментом диполя и совпадающий по направлению с вектором l.
С учетом того, что модуль вектора er единичной длины, (4.20) можно записать в скалярной форме
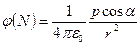 . (4.21)
. (4.21)
Конец радиуса – вектора r описывает в пространстве шаровую поверхность. Потенциал диполя в разных точках этой поверхности будет различен и, как видно из (4.21), определяется углом α. В частности, при α = 0, т.е. в направлении вектора l, потенциал равен
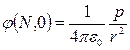 ,
,
а в направлении, перпендикулярном вектору l, когда α = π/2, 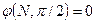 .
.
Полученный результат показывает, что потенциал на оси диполя меньше, чем для одиночного заряда одного знака, поскольку в знаменателе (4.21) стоит квадрат расстояния. А факт равенства нулю потенциала на плоскости, перпендикулярной вектору l, соединяющему заряды, естественен – потенциалы равные по величине, но противоположные по знаку взаимно компенсируются. Последнее, однако, не означает, что и напряженность поля E(α) при α = π/2 равна нулю. Вычислив grad φ(N) и задавшись α = π/2, получим величину так называемой поперечной компоненты напряженности поля, направленной параллельно вектору электрического момента:
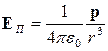 . (4.22)
. (4.22)
Если диполь с электрическим моментом p поместить во внешнее электрическое поле напряженностью EВ, то на заряды будут действовать силы, равные, согласно закону Кулона, по модулю qE, но противоположно направленные по направлению вектора напряженности EВ. Как известно из теоретической механики, пара противоположно направленных сил образует механический момент М, равный произведению силы на длину плеча, перпендикулярного действующим силам.
Модуль механического момента сил равен в нашем случае М = р·ЕВ·sinα, где α – угол между векторами электрического момента p и напряженности EВ. Момент М стремится повернуть диполь вдоль вектора напряженности EВ так, чтобы к зарядам, создавшим поле, ближе находился заряд диполя противоположного знака. Поскольку произведение модулей двух векторов на синус угла между ними есть модуль векторного произведения векторов, можно выражение момента записать в векторной форме:
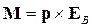 . (4.23)
. (4.23)
4.5. ПОЛЕ ДВИЖУЩИХСЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
4.5.1. Поле зарядов, движущихся линейно с постоянной скоростью
Рассмотрим систему большого количества электрически заряженных частиц положительной и отрицательной полярности, причем одни из них могут свободно перемещаться. Например, отрезок металлической проволоки, в которой электроны проводимости свободно перемещаются между положительными ионами, образующими кристаллическую решетку.
Под действием тепловой энергии электроны совершают хаотические движения внутри металла. Может ли реализоваться ситуация, когда в какой – то части проволоки окажется электронов больше, чем в другой? Ответ будет отрицательным, поскольку электростатические силы настолько велики, что из области избытка положительного заряда немедленно (а точнее, со скоростью света в вакууме) будет распространяться электростатическое поле, которое притянет электроны, компенсирующие положительный заряд. Следовательно, в проволоке никаких диполей образоваться не может, и электрическое поле вне проволоки равно нулю.
Если к концам проволоки приложить внешнее электрическое поле, то электроны начнут, в дополнение к тепловому движению, перемещаться по направлению, заданному напряженностью поля. У каждого электрона составляющая скорости вдоль проволоки своя, но поскольку их очень много, то можно говорить о некоторой средней скорости v.
Поместив вне проволоки неподвижный электрический заряд, можно убедиться, что внешнее электрическое поле отсутствует. Следовательно, в проволоке сохранилась равная плотность положительных и отрицательных зарядов. Если же внешний заряд движется с постоянной скоростью параллельно проволоке (или если расположить параллельно вторую проволоку с движущимися зарядами), то возникает силовое взаимодействие систем зарядов: при движении в одном направлении они притягиваются, а в противоположных – отталкиваются.
По аналогии с электрическим полем, считают, что движущиеся заряды образуют в пространстве силовое поле, названное магнитным. В чем его отличие от электрического?
Во–первых, не существует магнитных частиц, которые создают соответствующее поле. Поэтому напряженность поля должна иметь замкнутую форму вокруг порождающих его движущихся электрических зарядов; опыты подтверждают это предположение.
Во–вторых, магнитное поле воздействует только на движущиеся электрические заряды.
Экспериментально установлено, что вектор напряженности магнитного поля, названный магнитной индукцией В, направлен перпендикулярно плоскости, в которой лежат вектора скорости электрических зарядов v и радиус – вектор r к точке, в которой наблюдается поле. На рис. 4.4 показано направление векторов; коэффициент k = μ0/4πr3. Величина вектора индукции В, созданного зарядами q, движущимися линейно со скоростью v, равна
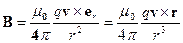 , (4.24)
, (4.24)
где В - вектор магнитной индукции, величина которого имеет размерность тесла (Т);
μ0 = 4π·10-7 Г/м - коэффициент, называемый магнитная постоянная (Г – сокращение от единицы индукции генри);
er – единичный вектор по направлению вектора r.
 С какой же силой действует магнитное поле на движущийся заряд q? Опыт показывает, что сила F по модулю пропорциональна величине заряда и его скорости, а по направлению перпендикулярна векторам скорости и магнитной индукции; в векторной форме эта зависимость имеет вид:
С какой же силой действует магнитное поле на движущийся заряд q? Опыт показывает, что сила F по модулю пропорциональна величине заряда и его скорости, а по направлению перпендикулярна векторам скорости и магнитной индукции; в векторной форме эта зависимость имеет вид:
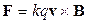 , (4.25)
, (4.25)
где k – константа, зависящая от выбора системы единиц.
Если заряды движутся в проводе, намотанном в виде катушки, называемой соленоидом, то вектор магнитной индукции В внутри ее будет направлен по оси соленоида. С какой силой будет воздействовать магнитное поле на электрический заряд, движущийся вдоль той же оси? Поскольку в данном случае угол между направлением скорости v и направлением вектора индукции В равен нулю, то и их векторное произведение равно нулю; следовательно, магнитное поле соленоида не оказывает силового действия на заряд, движущийся по его оси.
Если же электрические заряды движутся перпендикулярно вектору магнитного поля, то сила воздействия поля максимальна и, согласно (4.25), будет направлена перпендикулярно плоскости, в которых лежат вектора скорости v и индукции В.
4.5.2. Поле зарядов, движущихся с ускорением
В 1831г. Майкл Фарадей обнаружил, что изменяющееся во времени магнитное поле порождает электрическое. Если в переменное магнитное поле поместить проволоку, то под действием образовавшегося электрического поля электроны начнут перемещаться к одному из концов проволоки. Образуется диполь с разными потенциалами на концах. Это явление называется электромагнитной индукцией и используется в электротехнике для выработки электроэнергии в силовых генераторах.
Как показано в п.4.4, вокруг диполя в вакууме образуется электрическое поле, максимальное значение которого и направление задается формулой (4.22). Если электрическое поле Е изменять, т.е. сделать его переменным, то оно будет порождать магнитное с индукцией В, направленной перпендикулярно напряженности Е. Подобное поле называется электромагнитным. Правда, из (4.22) и (4.24) видно, что величина электрических и магнитных полей с удалением от диполя быстро спадает (см. знаменатели в указанных выражениях), но зато они существуют вне любого вещества, в вакууме, порождая друг друга.
Для уточнения параметров электромагнитного поля, рассмотрим систему, в центре которой расположен положительный заряд +q, относительно которого колеблется отрицательный заряд –q, перемещаясь периодически в крайние положения, определяемые концами вектора l на рис. 4.2.
Допустим, отрицательный заряд делает одно полное колебание за время Т, которое называется периодом колебаний. Количество колебаний за секунду f, называемое частотой колебаний, равно f = 1/Т и измеряется в герцах (Гц).
Чтобы записать колебания в виде тригонометрической функции, необходимо Т и f, т.е. секунды и герцы, заменить угловым выражением аргумента функции. Для этого достаточно учесть, что через время Т функция повторяет свои значения, т.е. период колебания эквивалентен полному углу 2π и, соответственно, любое промежуточное значение угла может быть задано следующим равенством: φ = 2π·t/Т или φ = 2π·f·t, где t – текущее время. Величина ω = 2π/Т = 2π·f имеет специальное название - угловая частота.
Теперь можно записать выражение для электрического момента диполя р в виде
p = -qlcosωt. (4.26)
Максимальное значение коэффициента перед косинусом называется амплитудой гармонической функции, в нашем случае амплитуда равна рм = ql.
Электрический момент диполя порождает переменное электрическое поле, которое, в свою очередь порождает магнитное, которое вновь порождает электрическое и т.д.
На перемещение зарядов в диполе затрачивается энергия. Во что она преобразуется (по закону сохранения энергии, просто исчезнуть она не может)?
Ответ на этот вопрос дает электродинамика. Уравнения электродинамики и последующие эксперименты показали, что энергия перемещения зарядов в диполе уносится электромагнитным полем в пространство. При этом вектор направления мощности излучения Р перпендикулярен векторам Е и В. На рис. 4.2 направление Р совпадает с направлением единичного вектора er (понятно, что излучение в равной мере идет и в направлении -er).
Конец вектора er при своем произвольном вращении описывает шар. Следовательно, электромагнитное излучение диполя образует колеблющееся электромагнитное поле, уносящее энергию по всем направлениям. Но в разных количествах: поскольку максимум напряженности электрического поля диполя находится на векторе, перпендикулярном оси диполя (см. выражение (4.22)), то в этом направлении излучается максимум энергии, по оси диполя – энергия излучения равна нулю; по остальным направлениям – некоторые промежуточные значения.
Укажем еще два важных вывода из уравнений электродинамики.
Первое. Излучаемая диполем мощность пропорциональна квадрату второй производной по времени от электрического момента, т.е.
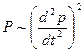 ,
,
или с учетом значения величины модуля р из (4.26)
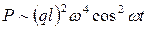 .
.
Из последнего выражения видно, что излученная мощность пропорциональна четвертой степени частоты; значит эффективно можно излучать только сигналы высокой частоты. Именно по этой причине все устройства радиосвязи работают на высокой частоте.
Второе. На большом удалении от диполя снижение максимальных значений (амплитуд) составляющих поля Ем и Вм происходит обратно пропорционально удалению r (а не r2) от диполя. Благодаря этому высокочастотное электромагнитное излучение распространяется на весьма большие расстояния. Скорость распространения электромагнитных волн в вакууме с = 3·108 м/с (300000 км/с).
В завершение этого раздела укажем, что инфракрасное излучение, видимый свет, рентгеновские лучи, γ – излучение являются электромагнитными волнами различной длины волны λ, которая равна скорости распространения с деленная на частоту f. Оказалось, что электромагнитные гармонические волны генерируются и воспринимаются приемниками различно в зависимости от их частоты.
Вопросы наложения случайного низкочастотного измерительного сигнала на высокочастотный гармонической (модуляция сигналов) для передачи совместно на большие расстояния будут рассмотрены в других дисциплинах.
Ниже в таблице приведены данные по электромагнитным волнам различных частот (совокупность частот называется спектром) и источникам их возбуждения [20].
Таблица 4.2.
Спектр электромагнитных волн
| Частота, f, Гц | Длина волны, λ, м | Название диапазона | Источники. Основные методы возбуждения |
| 103 до 1012 | 3·105 до 30·10-4 | Радиоволны | Переменные токи в проводниках и электронных потоках (генераторы радиочастот, генераторы СВЧ) |
| 1012 до 3,7·1014 | 8·10-7 | ИК - излучение | Излучение молекул и атомов при тепловых и электрических воздействиях |
| 3,7·1014 до 7,5·1014 | 4·10-7 | Видимый свет | |
| 7,5·1014 до 3·1017 | 1·10-9 | УФ излучение, мягкий рентген | Излучение атомов при воздействиях ускоренных электронов |
| 3·1017 до 3·1020 | 1·10-12 | Рентген, γ – излучение | Атомные процессы при воздействии ускоренных заряженных частиц |
| 3·1020 до 3·1023 | 3·10-15 | γ – излучение | Ядерные процессы, радиоактивный распад, космические процессы |
Дата добавления: 2015-04-29; просмотров: 1432;
