ДИЭЛЕКТРИКИ В НИЗКОЧАСТОТНОМ ЭЛЕКТРИЧЕСКОМ

ПОЛЕ

7.1. ОБЩАЯ ХАРАКТЕРИСТИКА ПРОЦЕССОВ

Диэлектрики, как сказано в гл. 6, имеют такую запрещенную энергетическую зону, что при умеренных напряженностях электрического поля (порядка 1 - 40 кВ/мм, пока не наступит пробой), электрический ток не проводят. Однако, как обнаружил Майкл Фарадей, введение диэлектрика между противоположно заряженными параллельными металлическими пластинами приводит к изменению разности потенциалов (напряжения) между ними. Но напряжение есть характеристика потенциальной энергии электрического поля. Куда же она делась?

Здесь возможны два варианта: или была совершена работа по переносу зарядов в поле, образованном между двумя металлическими пластинами, или внутри диэлектрика образовалось (индуцировалось) поле, направленное встречно полю пластин.

Поскольку в диэлектрике свободное движение зарядов невозможно, остается предположить возникновение индуцированного внутреннего поля диэлектрика. Эксперименты и последующий теоретический анализ подтвердил это предположение. Кратко рассмотрим физические процессы в системе из проводящих обкладок и диэлектрика между ними.

Предварительно необходимо определить полную напряженность поля в вакууме, создаваемую зарядами q. Другими словами, если окружить заряды q замкнутой поверхностью площадью А, то чему равна полная напряженность поля, называемая потоком вектора напряженности Е_П? Если замкнутая поверхность А имеет произвольную конфигурацию, то вычислить величину потока вектора по известному заряду q крайне сложно, поскольку необходимо знать величину и направление вектора напряженности в каждой точке поверхности А.

Задача резко упрощается, если учесть, что поток вектора одинаков через любую замкнутую поверхность, внутри которой находятся заряды q. Выберем замкнутую поверхность в виде сферы радиусом r c центром в точке расположения зарядов q. Тогда напряженность в каждой точке сферы будет направлена по нормали к поверхности и равна (см. раздел 4.4)

. (7.1)

Для определения потока вектора достаточно выражение (7.1) умножить на площадь сферы, равной 4πr². Получим значение потока Е_П через любую замкнутую поверхность вокруг зарядов q (ε₀ - электрическая постоянная)

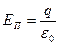. (7.2)

Теперь рассмотрим поле двух параллельно расположенных металлических пластин, заряженных равными зарядами противоположных знаков (рис. 7.1). Площадь пластин равна А, расстояние между ними – h.

Заряды равномерно растекаются по пластинам, создавая поверхностную плотность зарядов (количество зарядов на единицу площади) σ, равную для верхней пластины

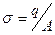(7.3)

и для нижней, соответственно

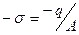. (7.4)

Поместим пластины в объем, изображенный на рис. 7.1 пунктирными линиями. Объем является замкнутым, следовательно, он охватывает полный поток векторов напряженности каждой из пластин.

Поток вектора напряженности верхней пластины будет равен q/2ε₀ вверх и такой же поток вниз; в целом, согласно (7.2), по объему q/ε₀. Для нижней пластины выражения аналогичны, только знаки потоков отрицательны.

Общий поток поля под нижней пластиной (область 1) Е₁ равен сумме потоков от верхней пластины Е/2 и нижней – Е/2 (поскольку направления векторов напряженностей совпадают):

Е₁ = q/2ε₀ + (- q/2ε₀) = 0.

По той же причине напряженность поля над верхней пластиной Е₃ = 0.

В области 2 между пластинами вектора напряженности направлены встречно, т.е. вычитаются, и поле будет равно

Е₂ = q/2ε₀ - (- q/2ε₀) = q/ε₀. (7.5)

Напряжение между пластинами U есть, согласно разделу 4.4, работа по переносу единичного заряда против сил поля на расстояние d между пластинами, т.е.

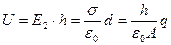. (7.6)

Система из двух проводящих обкладок, разделенных непроводящей средой, называется конденсатором, а коэффициент пропорциональности между величиной заряда q на пластинах конденсатора и напряжением U – емкостью конденсатора С:

q = СU, (7.7)

где

С = ε₀ А/h. (7.8)

Если в поле конденсатора внести диэлектрик, то заряды его атомов или молекул, до этого симметричные, начнут смещаться, образуя диполи. У симметричных молекул (например, Н₂, О₂, N₂) по направлению поля будут несколько смещаться орбиты электронов так, что центр суммарного отрицательного заряда молекулы не будет совпадать с координатами положительного заряда. У полярных молекул (типа Н₂О, СО, NH) существующие диполи будут поворачиваться по направлению внешнего поля. В любом случае образуется дипольный момент р, направленный навстречу вектору напряженности поля между пластинами конденсатора.

Общий дипольный момент молекул диэлектрика в единице объема называется вектором поляризации Р и он равен произведению числа молекул в единице объема N на дипольный момент одной молекулы, т.е. Р = Np.

Экспериментально установлено, что для большинства диэлектриков вектор поляризации пропорционален напряженности поля конденсатора Е_К, значение которого пока не известно (известна только напряженность поля в вакууме как поток Е₂ деленный на площадь пластин А):

,

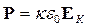где κ – константа, называемая диэлектрической восприимчивостью диэлектрика.

Напряженность поля в диэлектрике будет равна напряженности поля от плотности зарядов на обкладках минус поле, образованное диполями в единице объема, т.е.

,

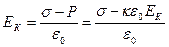откуда, после элементарных преобразований, получаем

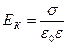, (7.9)

где ε = 1 + κ – безразмерная величина называемая диэлектрической проницаемостью среды.

Диэлектрическая проницаемость среды показывает во сколько раз напряженность поля в диэлектриках меньше, чем в вакууме при одинаковых величинах зарядов на обкладках конденсатора. Она для различных диэлектриков разная, но порядок величин следующий:

- у газов от 1,00027 (водород) до 1,00096 (углекислый газ);

- у жидкостей от 2,1 (керосин, скипидар, трансформаторное масло) до 81 (у воды);

- у твердых веществ от 2,0 (парафин, бумага) до 10 (слюда, стекло, мрамор).

Есть особый класс твердых веществ, называемых сегнетоэлектриками, у которых необычайно большая диэлектрическая проницаемость. Например, у титаната бария BTiO₃ проницаемость равна 1200.

Теперь можно вычислить напряжение заряженного конденсатора с диэлектриком

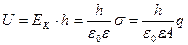, (7.10)

и, с учетом (7.7), его емкость

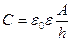. (7.11)

Последнее выражение показывает, какими параметрами конденсатора можно варьировать при разработке измерительных преобразователей: площадью обкладок А; толщиной диэлектрика (расстоянием между обкладками) h и диэлектрической проницаемостью ε.

Емкость конденсаторов измеряется в фарадах (Ф). Реальные ИП обладают незначительным диапазоном изменения емкости, порядка десятков (редко – сотен) пикофарад (1 пФ = 1·10^-12 Ф), что, конечно, усложняет достижение заданных метрологических характеристик [15].

Однако простота реализации, малые габариты и высокая временная стабильность преобразователей делают их привлекательными при разработке ИП многих физических величин в электрический сигнал.

7.2. ПИТАНИЕ ЕМКОСТНЫХ (КОНДЕНСАТОРНЫХ) ИП

Какой бы параметр емкостного преобразователя не изменялся под воздействием входной физической величины, очевидно, что получится параметрический ИП, не обладающий энергией для передачи в следующие преобразователи измерительной информации. Поэтому необходимо предусмотреть источник внешней энергии, питающий ИП.

Формально, в соответствии с (7.10), можно зарядить емкость каким – то точно известным зарядом и по изменению напряжения на обкладках судить об изменении параметра (расстояния h, площади A и т.д.) в функции от преобразуемой физической величины. Или подать на конденсатор точное значение напряжения и за выходной параметр принять количество зарядов.

Практически такой подход применяется крайне редко. Связано это с тем, что в реальных схемах измерения (подводящих проводах, входных каскадах последующих ИП) и в самих емкостных ИП существуют токи утечек и поддержать постоянство зарядов на обкладках какое-то время крайне сложно. Поэтому реально используются схемы, которые периодически восполняют потерю зарядов. Делается это или подачей на конденсатор гармонического [14] или импульсного тока [15].

Для понимания возникающих при этом вопросов рассмотрим простую схему питания емкостного ИП источником гармонического тока. Ток, как поступательное движение заряженных частиц через конденсатор (он называется током проводимости), конечно, отсутствует. Однако если во времени изменять величину и полярность напряжения на обкладках конденсатора, то будет изменяться напряженность поля в диэлектрике. А это, в соответствии с (7.9), ведет к изменению плотности зарядов на обкладках. Во внешней, подводящей цепи, изменение зарядов воспринимается как переменный электрический ток. Условный ток через диэлектрик конденсатора называется током смещения.

Подключим к конденсатору емкостью С источник гармонического сигнала

, (7.12)

где U₀ – амплитуда, т.е. максимальное значение сигнала относительно нулевого уровня;

ω – угловая частота, введенная в п. 4.5.2;

t – текущее время.

Величина заряда на конденсаторе, согласно выражению (7.7), будет изменяться во времени по закону

q(t) = Cu(t). (7.13)

Поскольку измеряемым параметром является ток в цепи, необходимо выражение (7.13) продифференцировать (напоминаем, что ток есть среднее количество зарядов, прошедших через поперечное сечение проводника dq за бесконечно малый интервал времени dt отнесенный к dt; см. раздел 5.3):

.

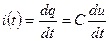В частном случае изменения напряжения по гармоническому закону, заданному в виде (7.12), величина тока перезаряда конденсатора равна:

. (7.14)

Следовательно, ток i(t) так же является гармонической функцией с той же частотой ω, что и напряжение. Запишем его, по аналогии с (7.12), в виде

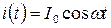; (7.15)

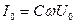- амплитудное значение тока.

Последнее выражение можно трактовать как закон Ома для участка цепи, связывающего значение тока через элемент цепи и падение напряжения на нем. Для амплитуд напряжения и тока связь имеет вид

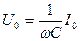. (7.16)

Величина Z_C = 1/ωC называется емкостным сопротивлением по аналогии с резистивным (омическим) сопротивлением. Принципиальное отличие емкостного сопротивления от омического заключается в его частотной зависимости: чем выше частота гармонической функции тока или напряжения, тем меньше емкостное сопротивление конденсатора.

Теперь можно сформулировать общие требования к источнику питания емкостного ИП: это должен быть генератор периодической функции точно известного вида (если это гармонический сигнал – то без искажения формы синусоиды) с постоянной амплитудой и постоянной частотой. Выполнение указанных требований усложняет разработку блоков питания по сравнению, например, с блоками питания для терморезистивных ИП.

Последнее существенное обстоятельство, которое необходимо отметить, заключается в том, что между проводами, подводящими и отводящими ток емкостного ИП, между электродами ИП и окружающими предметами образуются паразитные конденсаторы.

На рис. 7.2 приведена эквивалентная схема емкостного ИП, подключенного к генератору гармонического сигнала. Внутреннее сопротивление генератора обозначено Z_Г, напряжение u_Г = U₀sin ωt. Генератор нагружен на емкостные нагрузки, образованные емкостью преобразователя С_П, паразитными емкостями между проводами С₁₂, емкостями между электродами ИП и окружающими токопроводящими предметами С₁, С₂. Как правило, паразитные емкости бывают одного порядка с приращением емкости ИП под действием физической величины, и ток на нагрузке (входном сопротивлении последующего ИП2) i_П существенно отличается от тока с генератора i_Г.

Величину емкости С₁₂ можно сделать постоянной, если емкостной ИП окружить экраном (металлической сеткой, например), соединенным с общим проводом (общей землей) и функцию преобразования ИП определять в такой комплектации.

Влияние емкостей С₁ и С₂ на величину тока через емкостной ИП C_П так же можно быть исключено. Для этого необходимо обеспечить режим короткого замыкания на входе ИП2 и нулевое выходное сопротивление генератора гармонического сигнала, т.е. обеспечить выполнение условий Z_П = 0; Z_Г = 0.

Поясним это требование на примере входного сопротивления ИП2. Предположим, С₁₂ = 0 и ток через С_П равен i. Этот ток разветвляется на сумму токов: через емкость С₂ и через входное сопротивление ИП2 - i_П. Общее сопротивление цепи Z_О, подключенной к выходном электроду С_П, равно параллельному соединению входного сопротивления Z_П и сопротивления паразитной емкости С₂, равное Z_С = 1/(ωС₂):

.

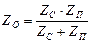Если Z_П = 0, то общее сопротивление нагрузки Z_О = 0 и влияние паразитной емкости исчезает. Физически полученный результат объясняется следующим образом: если после С_П имеется короткое замыкание (Z_П = 0), то нагрузкой генератора является только сопротивление С_П и ток, поступающий на ИП2 является только функцией величины емкости емкостного ИП.

Используя операционные усилители, рассмотренные в гл. 3, подключение емкостного ИП может быть реализовано по схеме рис. 7.3 (цепи питания операционных усилителей постоянным током условно не показаны).

Сигнал питания ИП подается на вход первого операционного усилителя А1, включенного по схеме повторителя. Обычно это гармонический сигнал с частотой порядка 10 кГц и амплитудой единицы вольт. Выходной сигнал ИП (емкости С_П) в виде тока поступает на второй каскад (операционный усилитель А2 с емкостной отрицательной обратной связью). Сопротивление R2 не имеет принципиального значения; оно необходимо (как и сопротивление R1) для стабилизации рабочей точки усилителя по постоянному току, т.е. для исключения дрейфа нуля. Выбирается величина сопротивления из условия отсутствия влияния на работу ИП по переменному току: R2 » Z_Co; Z_Co = 1/(ωC₀).

Гармонический сигнал u(t) = U₀ sin ωt поступает на вход А1 и в точности повторяется на выходе за счет действия цепи отрицательной обратной связи. Происходит это следующим образом. Предположим, часть тока с выхода А1 ответвляется паразитной емкостью провода на землю и напряжение u₁(t) на выходе А1 понижается относительно входного. Между входами усилителя появляется разность напряжения Δu = u(t) – u₁(t), которая усиливается до тех пор, пока напряжения на входах А1 не сравняются (Δu = 0), т.е. до выполнения условия u₁(t) = u(t).

Переменный ток, текущий через емкость преобразователя С_П полностью компенсируется током обратного знака, поступающего через емкость обратной связи С₀, что соответствует сформулированному выше условию подключения ИП к точке с нулевым сопротивлением.

Согласно результатам гл. 3, напряжение на выходе усилителя с отрицательной обратной связью u_В (t) связано с напряжением на входе u(t) зависимостью

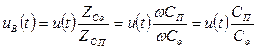. (7.17)

Выражение (7.17) показывает, что примененная схема включения ИП не только парирует влияние паразитных емкостей, но и обеспечивает линейность функции преобразования (связь между выходным напряжением схемы и изменением емкости ИП – С_П). И еще одно важное свойство рассматриваемой схемы: в правой части окончательного выражения (7.17) отсутствует частота гармонического сигнала, следовательно, погрешность преобразования не зависит от частотной нестабильности задающего генератора; достаточно обеспечить только амплитудную стабильность сигнала.

В технической литературе приводится много схем включения емкостных ИП, обладающих различными полезными свойствами. Цель проведенного анализа заключается в демонстрации проблем, возникающих при конструировании емкостных ИП, а именно: изготовлением конденсатора с переменной площадью электродов или диэлектрической проницаемостью среды разработка ИП не исчерпывается; появляется много дополнительных узлов, существенно влияющих на метрологические характеристики устройства.

7.3. ЕМКОСТНЫЕ ИП С ИЗМЕНЕНИЕМ ГЕОМЕТРИЧЕСКИХ

ПАРАМЕТРОВ

В соответствии с (7.11) изменение величины емкости ИП изменением геометрических параметров может достигаться или изменением площади обкладок A = A₀ ± ΔA, или расстоянием между ними h = h₀ ± Δh, где A₀, h₀ – среднее значение площади обкладок и расстояния между ними, а ΔA, Δh – приращения соответствующих величин.

Для выбора того или иного изменения параметра необходимо оценить линейность, чувствительность преобразования и диапазон изменения входной физической величины. При этом возможны два варианта: рассматривать изменение емкости от изменения входной физической величины или изменение емкостного сопротивления Z_С = 1/(ωС).

Итак, имеется два выражения, связывающие изменяемый параметр с величиной емкости:

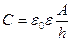(7.11)

и

. (7.12)

Чувствительность преобразования при изменении площади электродов на ΔA при выходном сигнале пропорциональном емкости равна

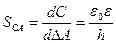, (7.13)

а при изменении расстояния между электродами

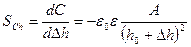. (7.14)

Аналогичным образом можно определить чувствительность при изменении емкостного сопротивления.

Оценим относительные чувствительности емкостных ИП для двух рассматриваемых случаев. Для этого разделим (7.13) на (7.14):

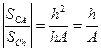. (7.14)

Если расстояние между обкладками конденсатора h много меньше их площади S, то предпочтительно параметром преобразования выбирать изменение расстояния между обкладками. Указанное обстоятельство определяет конструкцию емкостных ИП: если измеряемые линейные перемещения физического объекта малы (от десятка микрон до нескольких миллиметров), то используется ИП с изменением расстояния между обкладками. Например, емкостной ИП толщины диэлектрической пленки на поточной линии ее производства.

На рис. 7.4 показана часть емкостного датчика давления. Преобразователь давления в величину емкости состоит из двух камер. В первую поступает измеряемое давление Р, воздействующее на мембрану с жестким центром М. Вторая камера образована корпусом датчика и мембраной. На корпус нанесена пленка диэлектрика Д, а на нее напылена пленка металла, образующая с жестким центром мембраны две обкладки емкостного ИП.

Входное давление Р вызывает прогиб мембраны М и, тем самым, изменение емкости ИП. Использование жесткого центра обеспечивает параллельное перемещение части мембраны при ее прогибе под действием входного давления.

Если расстояния между обкладками конденсаторного ИП велики, то, согласно (7.14), ИП с изменением площади обкладок обеспечивают гораздо большую чувствительность.

Широкое применение ИП с изменением площади обкладок нашли при разработке измерителей уровня порошкообразных пищевых продуктов, зерна, цемента, песка, жидкостей (топлива, кислот, щелочей) в баках. Если сыпучие материалы или жидкости не электропроводны, то измеряют емкость между металлической стенкой бака и опущенным в него стержнем или тросом, изолированным от корпуса бака.

Пример выполнения емкостного уровнемера для токопроводящей жидкости (кислота, щелочь, растворы солей) приведен на рис. 7.5 [13].

В баке диаметром D и высотой h опущен металлический провод диаметром d₂, окруженный слоем диэлектрика диаметром d₁. Провод является одной обкладкой конденсаторного ИП. Вторая обкладка является переменной величиной, определяемой уровнем (высотой) жидкости х. От днища бака до верхнего слоя жидкости обкладкой является сама электропроводящая жидкость, и диэлектрическая проницаемость на этом участке будет определяться проницаемостью диэлектрика ε_r1. На интервале высот h - x второй обкладкой емкости ИП является корпус бака диаметром D, а диэлектрическая проницаемость среды определяется проницаемостью газа ε_r2, равной практически единице (см. раздел 7.1), и проницаемостью диэлектрика ε_r1.

В целом величина емкости определяется суммой параллельно включенных емкостей: емкости в газовой части бака С₁ и емкости заполненной жидкостью части бака – С₂:

.

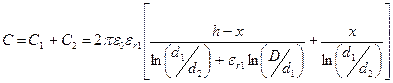В большинстве практических случаев D » d₁ и первым слагаемым в квадратных скобках можно пренебречь. Остается приближенное равенство, выражающее линейную зависимость емкости от высоты столба жидкости:

.

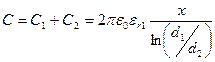7.4. ЕМКОСТНЫЕ ИП С ИЗМЕНЕНИЕМ ДИЭЛЕКТРИЧЕСКОЙ

ПРОНИЦАЕМОСТИ СРЕДЫ

Согласно выражению (7.11), изменение диэлектрической проницаемости среды ε между обкладками конденсатора изменяет величину емкости С. Как пример подобного ИП, рассмотрим емкостной сорбционный преобразователь влажности.

Измерения содержания влаги в газах, жидкостях и твердых материалах является наиболее массовым видом физико–химических измерений, и выполняются практически во всех отраслях промышленности.

Сорбционные ИП, выполненные напылением чувствительных слоев, появились в семидесятых годах, когда выяснилось, что основным фактором эксплуатационных отказов микросхем является натекание влаги через керамические и пластмассовые корпуса элементов. Для исследования процессов натекания паров воды и механизмов воздействия их на работоспособность микросхем, в корпуса начали встраивать емкостные ИП концентрации влаги; позднее разработанные конструкторские и технологические идеи были использованы для изготовления ИП в виде отдельных устройств.

ИП представляет собой изолирующую подложку размерами обычно не более 4 мм на 8 мм, покрытую пленкой металла (никелем, алюминием) толщиной несколько микрон. Поверх металлической пленки наносится слой пористого диэлектрика; чаще всего это пористая пленка двуокиси алюминия Al₂O₃ или полиамида. И, наконец, верхний слой – тонкий слой золота (порядка 1 мкм), проницаемый для паров воды (рис. 7.6).

Слой золота и металлическая подложка (на рисунке это никель) образуют обкладки конденсатора, а диэлектриком служит тонкая пленка окиси алюминия (ε_А = 8) или полиамида (ε_П = 3,6 – 5,0).

Пленки окиси алюминия (полиамида) содержат большое количество микроскопических пор, в которые проникают молекулы воды. Хотя поры занимают часть α площади поверхности А пленки, благодаря их глубине, общая поверхность сорбции увеличивается в сотни раз по сравнению с непористыми материалами. Поскольку диэлектрическая проницаемость воды ε_В = 81, то по мере накопления молекул воды в диэлектрическом слое увеличивается емкость конденсатора. Рассмотрим механизм изменения величины емкости подробнее на примере ИП с пленкой двуокиси алюминия (рис. 7.7).

Проникшие сквозь кристаллическую решетку золота молекулы воды адсорбируют на поверхности окиси алюминия, в основном на боковых поверхностях пор (поскольку площадь их поверхности много больше площади горизонтальной плоской поверхности А). Идет процесс физической сорбции, механизм которой кратко описанный в разделе 6.3.

Согла­сно теории сорбции, поры заполняются в несколько этапов. Первоначально, при небольшой влажности, стенки поры обволакиваются монослоями воды. После насыщения стенок пор молекулами воды, во - первых, умень­шается радиус пор (в поре образуется водяной «чулок»); во-вторых, на дне поры образуется водяной во­гнутый мениск. В районе мениска начинает конденсироваться жидкая фаза, хотя давление паров воды меньше давления насыщения р₀, т.е. давления, при котором пар конденсируется на гладкой горизонтальной поверхности большой площади.

Поясним сказанное выше. В п. 4.2.1 было указано, что газ при температуре ниже Т_КР может переходить в жидкое состояние и именно такое состояние газа называется паром. В частности, если поддерживать постоянную температуру замкнутого сосуда, частично заполненного водой, то над плоской горизонтальной поверхностью воды образуется паровая фаза (испарившаяся вода). Пар и вода находятся в состоянии динамического равновесия: сколько молекул воды переходит в пар, столько же возвращается в воду. При данной температуре Т₀ можно говорить о давлении насыщенного пара р₀. Данные для нескольких температур приведены в таблице:

Если при давлении паров 4,2 кПа понизить температуру сосуда (и содержимого) до 10⁰С, часть пара перейдет в жидкую фазу так, что давление оставшегося пара будет 1,2 кПа, т.е. будет иметь место процесс частичной конденсации пара.

А как ведет себя водяной пар в газе (например, в воздухе) с температурой Т_Г, предположим, при 30⁰С? Если пар находится при парциальном давлении р (например, при 1,2 кПа), меньшем давления насыщения р₀, то он ведет себя как газ. Понижение температуры Т_Г до значения, при котором данное парциальное давление пара р соответствует насыщению (в нашем примере это понижение температуры до 10⁰С), ведет к частичной конденсации пара; на внутренних стенках сосуда с газом начнет появляться пленка (или капли) воды.

В 1871 г. Кельвин установил, что в капиллярах, где поверхность воды криволинейна за счет эффекта поверхностного натяжения (образует мениск), пар конденсируется при давлениях меньших р₀. Им было получено уравнение, связывающее давление насыщения над мениском р с давлением насыщения над горизонтальной поверхностью воды р₀:

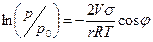, (7.15)

где V - молярный объем воды;

σ – коэффициент поверхностного натяжения воды при температуре Т;

r – радиус капилляра (или поры в пористом материале);

φ – краевой угол мениска воды со стенками поры; в расчетах принимают φ = 0;

R – универсальная газовая постоянная;

Т – абсолютная температура.

Теперь становится понятно, почему в микропорах конденсируется жидкая фаза воды, хотя температура пара выше насыщения над гладким зеркалом воды. Для примера, определим, при каком радиусе пор наступит насыщение, если парциальное давление пара равно 1,2 кПа, а окружающая температура - плюс 30⁰С (Т = 303,16 К).

Вода при указанной температуре имеет коэффициент поверхностного натяжения σ = 71,2·10^-3 Н/м и молярный объем ее V = 18·10^-6 м³/моль. Подставим данные в выражение (7.15):

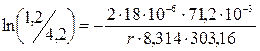, откуда r ≈ 0,8·10^{-9 м.}

Полученные результаты позволяют сделать два вывода.

Первый – диэлектрик в ИП должен иметь вполне определенный размер пор. В порах малого диаметра (если условно считать их форму цилиндрической) при меньших давлениях пара начинается его конденсация и, как следствие, растет чувствительность преобразователя. Для справки – радиус молекулы воды равен 0,15·10^{-9 м. Если использовать такой высококачественный диэлектрик как слюда (поверхность не содержит пор) или высококачественный сорбент силикагель (поры от одного до тысячных долей миллиметра), чувствительность преобразователя будет крайне низка: и в первом и во втором случаях не будут конденсироваться пары воды. В первом случае из – за отсутствия пор, во втором – поры слишком большого диаметра.}

Второй вывод. Поскольку в уравнения сорбции и конденсации входит температура, то необходимо исключить влияние этого дестабилизирующего фактора. Это можно сделать либо помещая ИП в термостат с постоянной температурой, либо вводя второй канал измерения, содержащий преобразователь текущей температуры емкостного ИП. Как правило, для стационарных измерителей, питающихся от сети, используют первых путь, а для переносных приборов, питающихся от батареек – второй.

Исходя из описанного механизма работы емкостного ИП влагосодержания, его функция преобразования (зависимость величины емкости конденсатора от влагосодержания окружающей среды) при произвольной влажности равна [16]:

, (7.16)

где ε_о - диэлектрическая проницаемость вакуума;

e_S - диэлектрическая проницаемость твердой Al₂O₃ (e_S = 8);

e_а - диэлектрическая проницаемость воздуха (e_а = 1);

А - площадь сенсора;

a - пористость пленки;

d - толщина барьерного слоя;

l – средняя длина пор, на которой может происходить конденсация воды;

B – средняя длина пор, заполненных газом;

e_в - диэлектрическая проницаемость барьерного слоя;

X - часть пор, заполненных водой (X = aA).

Первое слагаемое в правой части является постоянной величиной, определяемой конструктивными параметрами ИП - диэлектрической проницаемостью диэлектрика, толщиной барьерного слоя и т.д. Второе слагаемое описывает изменение емкости в функции от доли пор, заполненных водой при данном парциальном давлении пара в окружающем газе.

Для измерения влагосодержания при малых парциальных давлениях пара, необходимо использовать диэлектрик с еще меньшим средним диаметром пор, чем у окиси алюминия. Например, для измерения микровлажности используют емкостной ИП с диэлектриком из тонкой пленки окиси кремния.