ПОСТОЯННЫМ ЭЛЕКТРИЧЕСКИМ ПОЛЕМ
5.1. ПОСТАНОВКА ЗАДАЧИ
В главе 4 были рассмотрены некоторые особенности электрического и электромагнитного полей. При этом не обсуждались вопросы, откуда берутся заряды, что их удерживает на расстоянии друг от друга, каким образом можно заряды перемещать против сил поля, создавая электромагнитные колебания различных частот. Подробное рассмотрение указанных вопросов выходит за рамки данного курса.
Укажем только, что затратой механической, химической, тепловой энергии в электрогенераторах, аккумуляторах, солнечных элементах можно разделить электрические заряды так, что на двух разнесенных выходах будут разные потенциалы.
Образовавшееся электрическое поле взаимодействует с веществом, создавая различные эффекты в зависимости от напряженности поля, вида и состояния вещества, наличия других сопутствующих полей и т.д.
В данном курсе не ставится задача описать и объяснить все возможные эффекты взаимодействия электрического поля и вещества, а показать, как они могут быть использованы для создания измерительных преобразователей с выполнением основных требований, сформулированных в п. 2.8.
Даже в такой, более узкой, постановке, рассмотреть все многочисленные эффекты не представляется возможным. Поэтому далее не будут рассматриваться эффекты, связанные с измерением электрических и электромагнитных параметров (напряжение, мощность, частота, фазовые сдвиги и т.д.), поскольку большая часть из ИП электрических величин рассматриваются в других дисциплинах. А среди эффектов, связанных с преобразованием неэлектрических физических величин, будут рассмотрены наиболее часто используемые в промышленных системах измерения.
5.2. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТАЛЛОВ
К металлам относится большая группа элементов таблицы Менделеева (86 из 106 элементов таблицы) и их соединения (сплавы), отличительными свойствами которых являются высокая электропроводность и теплопроводность. В твердом состоянии металлы, как правило, имеют кристаллическую структуру: в узлах кристаллической решетки располагаются ионы с положительным зарядом. Электроны самой последней от ядра орбиты (валентные электроны) настолько слабо связаны с ионами, что под действием окружающей температуры (температура, как известно, есть мера квадрата скорости электронов) отрываются от своих атомов и хаотично, подобно газу, перемещается в межкристаллическом пространстве. Плотность свободно перемещающихся электронов (называемых электронами проводимости) составляет порядка 1022 – 1023 в 1 см-3, что в 150 раз больше, чем число молекул газа в том же объеме при атмосферном давлении.
Сохраняют свою форму твердые тела и, в частности, металлы, благодаря действию электростатических сил, описанных в гл. 4. На большом удалении атомов друг от друга действуют силы притяжения между отрицательно заряженными электронами оболочек и положительно заряженными ядрами соседних атомов. По мере сближения атомов электростатические силы нарастают, усиливая эффект. Поскольку атомы являются сложной системой электрических зарядов, сила их взаимодействия F определяется не законом Кулона, а величиной, пропорциональной седьмой степени расстояния, т.е. сила взаимодействия быстро спадает с ростом расстояния r: F ~ k/r7.
 На рис. 5.1 показана зависимость силы электростатического взаимодействия между двумя атомами F как функция расстояния r [11]. Видно, что по мере сближения атомов сила притяжения растет. Но при этом начинают существенно влиять силы отталкивания между положительно заряженными ядрами и общий эффект притяжения ядер убывает до тех пор, пока суммарная сила взаимодействия на расстоянии d между ядрами не станет равна нулю. При дальнейшем сближении атомов силы отталкивания быстро нарастают.
На рис. 5.1 показана зависимость силы электростатического взаимодействия между двумя атомами F как функция расстояния r [11]. Видно, что по мере сближения атомов сила притяжения растет. Но при этом начинают существенно влиять силы отталкивания между положительно заряженными ядрами и общий эффект притяжения ядер убывает до тех пор, пока суммарная сила взаимодействия на расстоянии d между ядрами не станет равна нулю. При дальнейшем сближении атомов силы отталкивания быстро нарастают.
Временное постоянство и неизменность формы металлов, их сопротивление сжатию и растяжению определяются силами электростатического взаимодействия между атомами.
В области d равенства сил притяжения и отталкивания имеется небольшой участок, в пределах которого функция F(r) линейна. Это означает, что после сжатия или растяжения, например, металлического стержня длиной l на малую длину Δl, он восстановит свой размер l. Этот эффект называется упругой деформацией и позволяет изготавливать упругие узлы ИП (мембраны, пружины, сильфоны и т.д.). Отношение приращения длины Δl к самой длине l называется относительным удлинением ε = Δl / l.
Внешняя сила FВ, необходимая для деформации стержня с единичной площадью поперечного сечения называется нормальным напряжением σ (размерность – Па). Если площадь поперечного сечения стержня обозначить через S, то
σ = FВ/S.
В пределах области упругой деформации тел относительная деформация и нормальное напряжение связаны между собой законом Гука:
σ = Е·ε, (5.1)
где Е – постоянная для каждого металла величина (размерность – Па), называемая модулем упругости или модулем Юнга; для большинства образцов стали Е ≈ 2·1011 Па.
Смысл модуля упругости можно понять, если положить ε = 1: это напряжение, которое необходимо приложить к стержню для удвоения его длины. Конечно, реально никогда такое напряжение к образцам не прикладывается – они будут деформированы безвозвратно или разрушатся; обычно величина ε не превышает значений 0,001 – 0,005.
В процессе упругой деформации изменяется не только длина стержня l, но и его поперечные размеры. Экспериментально установлено, что в пределах упругой деформации относительное изменение поперечных размеров стержня 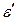 , отнесенное к относительной продольной деформации ε, для данного материала есть величина постоянная, называемая коэффициентом поперечной деформации или коэффициентом Пуассона μ:
, отнесенное к относительной продольной деформации ε, для данного материала есть величина постоянная, называемая коэффициентом поперечной деформации или коэффициентом Пуассона μ:
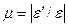 . (5.2)
. (5.2)
Для большинства металлов μ ≈ 0,3.
С воздействием механической силы на металлический образец связан еще один эффект: изменение геометрических размеров образца (например, при растягивающих усилиях длина стержня увеличивается, а поперечное сечение уменьшается) приводит к изменению его электрического сопротивления. Это явление называется тензорезистивным эффектом. Его мы рассмотрим подробнее позднее, но уже сейчас можно заметить, что, тензоэффект позволяет силы (или давления) преобразовать в изменение электрического сопротивления проволоки.
5.3. ЭФФЕКТЫ ПРИ ВОЗДЕЙСТВИИ ВНЕШНЕГО
ЭЛЕКТРИЧЕСКОГО ПОЛЯ НА МЕТАЛЛ
Предположим, имеется устройство, которое затратой своей энергии разделяет электрические заряды (например, гальванический элемент). На клеммах устройства имеются потенциалы φ1 и φ2. Нас интересуют потенциалы (а не напряженность поля), поскольку их разность φ1 - φ2 определяет ту работу, которую могут совершить заряды в данном поле (см. уравнение (4.17)).
Разность потенциалов, как указывалось выше, называется напряжением U: U = φ1 - φ2, единица измерения – вольт (В). Если клеммы соединить между собой металлической проволокой, то под действием разности потенциалов электроны проводимости станут перемещаться от одной клеммы к другой. Поскольку устройство продолжает затрачивать энергию (в нашем примере – химическую) на разделение зарядов и поддержание разности потенциалов, в проводнике установится стационарный поток электронов, называемый электрическим током. Величина тока I определяется как отношение числа зарядов (электронов) Δq, переместившееся через поперечное сечение проводника за время наблюдения Δt:
I = Δq/ Δt; (5.3)
размерность единицы силы тока - ампер (А).
В более общей записи, с учетом возможного изменения числа зарядов, проходящих через поперечное сечение проводника в единицу времени, ток определяется выражением
I = dq/dt. (5.4)
Ток I, протекающий через единицу поперечной площади проводника называется плотностью тока j:
j = I / S, (5.5)
где S – площадь поперечного сечения проводника.
Исходя из представлений о свободных электронах в металлах, Пауль Друде предположил, что электроны проводимости в металле ведут себя подобно молекулам идеального газа. В промежутках между соударениями они движутся совершенно свободно, пробегая в среднем некоторый путь λ. Длина пробега электронов, в отличие от газов, где соударяются молекулы, ограничивается соударениями с ионами, образующими кристаллическую решетку металла. В процессе столкновений устанавливается тепловое равновесие между электронным газом и кристаллической решеткой.
Согласно кинетической теории газов, каждая частица движется хаотически, меняя свою скорость и направление движения после каждого соударения. Поэтому средняя скорость электронов по любому направлению равна нулю.
Но энергия частиц определяется квадратом скорости, которая не может быть отрицательной. Под средней скоростью частиц понимают именно корень квадратный из усредненных квадратов скоростей. Обозначается эта средняя скорость обычно так 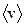 и равна
и равна
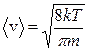 , (5.6)
, (5.6)
где k = 1,38·10-23 Дж/К – постоянная Больцмана;
Т – абсолютная температура;
m = 9,1·10-31 кг – масса электрона.
При комнатной температуре (~300 К) средняя скорость электронов проводимости по формуле (5.6) имеет значение:
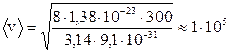 м/с.
м/с.
При включении внешнего электрического поля на хаотическое тепловое движение электронов, происходящее со средней скоростью 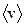 , накладывается упорядоченное их движение с некоторой средней скоростью
, накладывается упорядоченное их движение с некоторой средней скоростью 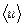 , величина которой может быть оценена, исходя из формулы плотности тока
, величина которой может быть оценена, исходя из формулы плотности тока
j = ne 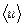 , (5.7)
, (5.7)
где е = 1,6·10-19 Кл – заряд электрона.
Предельно допустимая техническими нормами плотность тока для медных проводов составляет около 107 А/м2 (10 А/мм2). Подставим в последнее выражение значение плотности тока и указанную в п. 5.2 плотность электронов n = 1·1029 м-3. Получим оценку величины средней скорости электронов под действием электрического поля 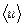 ≈ 10-3 м/с. Видно, что вклад направленного движения электронов существенно (в 108 раз) меньше их средней скорости теплового движения.
≈ 10-3 м/с. Видно, что вклад направленного движения электронов существенно (в 108 раз) меньше их средней скорости теплового движения.
Вызываемое полем изменение среднего значения кинетической энергии электронов определяется из следующих соображений.
Средний квадрат результирующей скорости равен
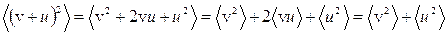 .
.
Сомножитель при коэффициенте 2 равен нулю, поскольку средняя скорость теплового движения v равна нулю, о чем говорилось выше.
Среднее увеличение кинетической энергии электронов в за счет действия внешнего поля составляет
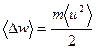 . (5.8)
. (5.8)
Для оценки приращения энергии необходимо в (5.8) оценить величину средней скорости ‹u›. Предположим, что поле, ускоряющее электроны, однородно и имеет модуль напряженности, равный Е. Тогда под действием поля электрон будет двигаться с ускорением еЕ/m, пока, пролетев в среднем расстояние λ, не ударится об ион и не передаст ему свою энергию. Если считать, что после предыдущего соударения электрон начинает движение с нулевой скоростью, то максимальное значение скорости упорядоченного движения составит в среднем
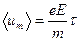 ,
,
где τ = λ/‹v› — среднее время между двумя последовательными соударениями электрона с ионами решетки; в выражении учтено, что |v + u| практически равно |v|.
Заменив в последнем выражении τ его значением, и учтя, что средняя скорость равна половине максимальной (поскольку минимальная равна нулю), получим окончательно
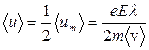 . (5.9)
. (5.9)
Подстановка этого выражения в формулу (5.7) дает значение плотности электрического тока в проводнике
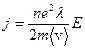 . (5.10)
. (5.10)
Полученное выражение есть одна из форм записи закона Ома для участка цепи: плотность тока j пропорциональна напряженности поля E. Придадим, однако, последней формуле другой вид. Для этого умножим и разделим ее на длину провода l и площадь поперечного сечения S:
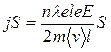 .
.
Слева, согласно (5.5), стоит выражение тока I, а справа произведение leE выражает работу по переносу зарядов в электрическом поле. С учетом того, что работа равна разности потенциалов (напряжению) U, уравнение приобретает вид:
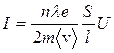 . (5.11)
. (5.11)
Коэффициент при U, показывающий какое сопротивление оказывает кристаллическая решетка упорядоченному движению электронов, называется электрической проводимостью; чаще на практике используется обратная ей величина, называемая омическим (резистивным) сопротивлением R
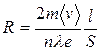 . (5.12)
. (5.12)
Закон Ома получает традиционный вид I = U/R.
Величина
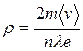 , (5.13)
, (5.13)
определяющая сопротивление проводника единичной длины и единичной площади называется удельным сопротивлением.
Рассмотрим выражение (5.12) с точки зрения возможности реализации измерительных преобразователей.
Допустим, имеется проволока длиной l, площадью поперечного сечения S и сопротивлением R. Приложим к концам проволоки растягивающую силу F. Проволока деформируется; по закону Гука ее длина увеличится на Δl = l·ε, где ε – относительное удлинение из (5.1), а площадь S уменьшится (с учетом коэффициента Пуассона) на ΔS ~ S·0,1·ε2. Общее сопротивление проводника изменится и станет равным
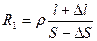 .
.
Следовательно, если к проволоке приложить силу в пределах упругой деформации, получится преобразователь силы в омическое сопротивление на основе тензоэффекта. Учитывая малую величину относительных приращений линейных размеров при упругой деформации, сразу можно отметить, что тензоэффект весьма незначительно изменяет первоначальную величину сопротивления. Это, конечно, серьезный недостаток. Есть два пути его преодоления – поискать другой физический эффект преобразования деформаций в электрический параметр или использовать измерительные усилители, рассмотренные в главе 3, для усиления выходного сигнала ИП.
Теперь проанализируем выражение (5.13) под тем же углом зрения, т.е. возможности использовать свойства металлического проводника в постоянном электрическом поле для создания ИП. Здесь просматриваются две возможности.
Первая связана с зависимостью средней скорости электронов ‹v› от температуры проволоки (см. выражение (5.6)). С ростом температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решетки, что приводит к уменьшению длины свободного пробега λ электронов проводимости. Внешне это проявляется как зависимость удельного сопротивления от температуры (терморезистивный эффект).
В широком диапазоне температур зависимость ρ = ρ(Т) нелинейная; но можно подобрать металлы (медь, платина, никель), для которых в диапазоне температур от 200 до 800 К указанная зависимость близка к линейной и имеет вид:
ρ = ρ0 [1 + α(T – T0)], (5.14)
где ρ0 – удельное сопротивление проволоки при некоторой начальной температуре Т0 (обычно за начальную температуру принимают 00 С);
α – температурный коэффициент сопротивления; числовое значение его для меди и платины близко к 0,004 Ом/К.
Вторая возможность создания ИП связана с наличием в выражении (5.13) концентрации свободных электронов n. При постоянной температуре средние скорости электронов проводимости у разных металлов примерно одинаковы, но концентрации электронов различны. Если создать контакт двух проводников из разных металлов (например, сварив их концы), то электронный газ из металла с более высокой концентрацией электронов будет переходить в металл с меньшей их концентрацией. На концах проводников возникнет разность потенциалов тем большая, чем выше разность температур между местами контактов. Это явление называется эффектом Зеебека, по фамилии физика, открывшего его в 1821г.
Описанные выше эффекты не исчерпывают всех исследованных в физике проявлений взаимодействия электрического поля с металлами (их более 20), но перечисленные выше используются чаще других при разработке ИП.
Наличие некоторой однозначной зависимости омического сопротивления проводника или напряжения на концах спая двух проводников от воздействия физической величины другой природы (температуры, силы) является только предпосылкой, а не гарантией разработки соответствующего ИП. Связано это с тем, что вместо весьма сложных взаимовлияющих физических процессов в металлах и сплавах, выше рассматривались их предельно упрощенные модели.
Поэтому необходимо, хоть и весьма сжато, оценить возможность реализации ИП на соответствующем эффекте так, чтобы выполнить требования п. 2.8 (линейность функции преобразования, минимум основной погрешности, незначимость динамической погрешности, слабое влияние неинформативных параметров и окружающей среды и т.д.).
5.4. ИП НА ОСНОВЕ ЭФФЕКТА ЗЕЕБЕКА
ИП на основе эффекта Зеебека называется термоэлектрическим преобразователем, или, короче, термопарой.
Итак, на концах спая двух разнородных металлов 1 и 2 при температуре Т образуются разные потенциалы, определяемые концентрацией электронов проводимости n01 и n02 соответственно в каждом из них. При этом принимается, что указанные электроны перемещаются в кристаллической решетке как идеальный газ. Согласно кинетической теории идеального газа, давление его при температуре Т равно p = n0kT, где n0 - концентрация электронов, k – постоянная Больцмана (см.п. 4.2.1).
Даже если температуры обоих металлов одинаковы, но 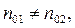 то давления электронного газа в них различны. Примем для определенности, что давление р1 > р2; тогда под действием перепада давлений р1 - р2 электроны будут переходить из первого металла во второй в большем количестве, чем из второго в первый. Это будет происходить до тех пор, пока электрическое поле, возникающее вследствие преимущественного перехода электронов, не компенсирует своим противодействием влияния перепада давления. Контактная разность потенциалов Δφ12, которая возникает на границе двух металлов в результате перехода электронов, выражается формулой
то давления электронного газа в них различны. Примем для определенности, что давление р1 > р2; тогда под действием перепада давлений р1 - р2 электроны будут переходить из первого металла во второй в большем количестве, чем из второго в первый. Это будет происходить до тех пор, пока электрическое поле, возникающее вследствие преимущественного перехода электронов, не компенсирует своим противодействием влияния перепада давления. Контактная разность потенциалов Δφ12, которая возникает на границе двух металлов в результате перехода электронов, выражается формулой
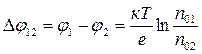 , (5.15)
, (5.15)
где φ1 и φ2 – потенциалы на конце металла 1 и 2 соответственно.
Уравнение (5.15) демонстрирует два свойства эффекта Зеебека, делающие его привлекательным для создания генераторного ИП температуры:
- напряжение (разность потенциалов Δφ12) зависит только от отношения концентраций электронов, т.е. от химических свойств металлов; в уравнение не входят ни длина проводов, ни площадь их поперечного сечения и т.д. Это позволяет использовать очень тонкие провода, достаточно обеспечить их механическую прочность. Как следствие, ИП оказывается миниатюрным и быстродействующим, т.е. исключается динамическая погрешность преобразования;
- напряжение зависит от температуры линейно, а это позволяет предположить линейность функции преобразования разрабатываемого ИП.
Как правило, провода, из которых изготавливают термопару, химически отличны от проводов, которыми термопара соединяется с вольтметром или другим измерительным средством, преобразующим для потребителя напряжение в величину измеряемой температуры. Поэтому важно установить, как влияют дополнительные провода на конечную разность потенциалов.
Возьмем последовательно соединенные 4 провода из различных металлов (рис. 5.2) и рассмотрим образовавшиеся потенциалы φ1, φ2, φ3, φ4 на границах их раздела. Термопару образуют провод 1 и 4. Разность потенциалов φ1 - φ4, с учетом того, что каждый внутренний проводник имеет свой потенциал, равна:
 φ1 - φ4 = (φ1 - φ2) + (φ2 - φ3) +(φ3 - φ4).
φ1 - φ4 = (φ1 - φ2) + (φ2 - φ3) +(φ3 - φ4).
Раскрыв скобки в правой части выражения, получим результат, совпадающий с (5.15):
Δφ14 = φ1 – φ4 ,
что позволяет сделать вывод: разность потенциалов на концах термопары не зависит от наличия промежуточных проводников и спаев. Полученный вывод сильно упрощает требования к построению измерительных каналов с термопарами – отпадает необходимость задавать какие-то обязательные требования к проводникам, соединяющим термопару с последующим измерительным прибором или ИП (например, усилителем).
Нужно, однако, четко понимать, при каких ограничениях сделан последний вывод – все промежуточные проводники и спаи находятся при одной и той же температуре. Если температуры для разных спаев различны, то общей компенсации промежуточных термо э.д.с. не будет иметь места.
Теперь можно изобразить простейшую измерительную цепь, включающую термопару (рис. 5.3). Она состоит из термопары (провода 1 и 2), милливольтметра (или промежуточного ИП) и соединительных проводов от него до термопары. Один спай у термопары, называемый горячим спаем (Г.С), реализован сваркой или пайкой проводников 1 и 2. Второй спай, называемый холодным спаем Х.С., непосредственно у термопары не соединен, к нему подключаются провода (чаще всего медные), присоединяющие измерительный прибор (или последующий ИП).

Горячий спай при измерениях погружают в исследуемую среду (печь нагревательного котла, камеру сгорания двигателя и т.д.), а концы холодного спая, расположенного вне зоны исследуемой среды, подключают к последующим средствам измерения.
Как было ранее показано, промежуточные провода не влияют на разность потенциалов термопары, поэтому можно считать, что провода 1 и 2 холодного спая соединены так же, как и горячего.
Оценим напряжение, развиваемое термопарой на входе в милливольтметр (поскольку сопротивление горячего спая порядка 30 - 60 Ом, а входное сопротивление милливольтметра десятки кОм, будем считать, что термопара подключена к бесконечно большому сопротивлению). В рассматриваемой цепи два источника напряжения: напряжение горячего спая UГ и напряжение холодного спая UХ. Общее напряжение равно алгебраической сумме напряжений. Согласно (5.15)
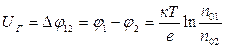 ;
; 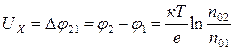 ,
,
а их сумма U будет равна
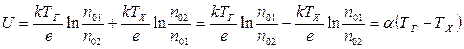 . (5.16)
. (5.16)
В последнем выражении через ТГ и ТХ обозначены температуры соответственно горячего и холодного спаев; коэффициент α называется удельной термо-э.д.с. и равен
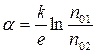 . (5.17)
. (5.17)
В выражение (5.17) входят постоянная Больцмана k, заряд электрона e и концентрации электронов в термоэлектродах n01 и n02, слабо изменяющиеся в широком диапазоне температур (примерно от 200 до 1000 К). Поэтому можно считать удельную термо–э.д.с. α величиной постоянной. В таком случае уравнение (5.16) описывает линейную функцию преобразования: напряжение на концах холодного спая U пропорционально разности температур (ТГ – ТХ). В частном случае нахождения спаев при равной температуре напряжение U = 0.
Линейность функции преобразования очень ценное свойство, но есть в выражении (5.16) указание и на сложность, которая становится очевидной, если раскрыть скобки: U = αТГ - αТХ. Первое слагаемое есть напряжение от измеряемой температуры, а второе – напряжение, пропорциональное температуре окружающей среды вне зоны измерения. В терминах гл. 2 это аддитивная составляющая погрешности преобразования, которую нельзя оставить без внимания.
Для примера положим, что в топке котла измеряется температура порядка ТГ = 9000С. От корпуса топки идет тепловой поток и в области холодного спая (вне котла) температура равна ТХ = 800С. В итоге напряжение на выходе термопары будет, согласно (5.16), пропорционально не 9000С, а 8200С, что, конечно, недопустимо.
Чтобы исключить указанную составляющую погрешности, схему измерения приходится существенно усложнять: или помещать холодный спай в термостат с известной температурой (например, 00С), или другим ИП температуры, например, термометром сопротивления, измерять температуру холодного спая и в результаты измерений вводить соответствующую поправку.
Теперь оценим крутизну функции преобразования α. Величины заряда электрона и постоянной Больцмана приводились ранее, остается оценить величину логарифма в выражении (5.17). Концентрации электронов пропорциональны валентности металлов и различаются в 2 - 4 раза. Поэтому логарифм отношения концентраций близок к единице. Исходя из этого
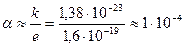 В/К.
В/К.
При столь малой крутизне преобразования (при изменении температуры на 1000 К выходное напряжение изменится на U ≈ 0,1 В), выходное напряжение термопары будет составлять сотые доли вольта. Канал измерения вновь, в дополнение к термостату, приходится усложнять, вводя в него усилители и устройства подавления помех. Усилители были рассмотрены в гл. 3, а подавители помех будут изложены в последующих курсах (один из простых приемов будет изложен в п. 8.1).
В заключение приведем данные по наиболее распространенным в промышленности серийным термопарам. Большая часть из них изготавливается не из чистых металлов, а из сплавов, специально разработанных для этой цели. Название термопары состоит из слова «термопара» и наименования материала проводов. Например: ТХА – термопара хромель – алюмель.
Таблица 5.1.
Данные по промышленным термопарам
| Наименова-ние термопары | Материал проводов | Отличительные особенности | Диапазон преобразова-ния, 0С | Термо-э.д.с. в конечных точках, мВ |
| Хромель – алюмель (ТХА) | Алюмель: никель + алюминий(2%) + кремний(1,3%) + марганец (2,3%) + кобальт (1,9%). Хромель: никель + хром (9%) + кобальт (1%). | Наиболее линейная функция преобразования | - 50,0 до 1300,0 | - 1,889 до 52, 398 |
| Хромель – копель (ТХК) | Копель: медь + никель, кобальт (43,5%) + марганец (0,1 – 1,0%). | Большая термо - э.д.с. | - 50,0 до 800,0 | - 3,11 до 66,42 |
| Железо – константан (ТЖК) | Константан: медь + никель (40%) + марганец (1,5%). | Устойчива в окислительных средах | -100,0 до 800,0 | - 4,63 до 45,53 |
5.5. ИП НА ОСНОВЕ ТЕРМОРЕЗИСТИВНОГО ЭФФЕКТА
С изменением температуры металлической проволоки изменяется ее удельное сопротивление примерно по линейному закону (5.14)
ρ = ρ0 [1 + α(T – T0)].
Реально берут проволоку из особо чистой платины, меди или никеля и наматывают катушку с тем, чтобы сопротивление ее было в диапазоне от 10 до 1000 Ом. Функция преобразования температуры в сопротивление имеет вид
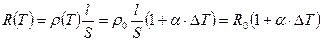 , (5.18)
, (5.18)
где α - температурный коэффициент сопротивления;
ΔТ =Т – Т0.
Коэффициент сопротивления в общем виде зависит от температуры α(Т), поскольку вместе с температурой меняются величины удельного сопротивления ρ0, длина l и площадь поперечного сечения S. Для оценки величин, на которые может изменяться температурный коэффициент, укажем, что для платины в области 273 К (00С) α(273) = 0,004 К-1, а в области 20 К α(20) = 0,0004 К-1, т.е. на порядок меньше.
Размерность К-1 означает, что проводник, с сопротивлением 1 Ом, при изменении температуры на 1 К изменит начальное сопротивление на 0,004 Ом. Если ИП имеет начальное значение сопротивления не один, а R0 Ом, то приращение его при изменении температуры на 1 К составит R0 · 0,004 Ом.
Статические характеристики термометров сопротивления (особенно платиновых) тщательно исследуют, поскольку это самые точные ИП температуры промышленного применения. Когда речь идет об измерениях с погрешностью менее 0,01 – 0,001 К, использовать линейную модель функции преобразования не представляется возможным. Международная температурная шкала 1990 г. (МТШ – 90) устанавливает следующие уравнения функции преобразования для платиновых термометров:
- в области температур от 13,8 К (температура, при которой водород находится в трех равновесных фазах – жидкой, твердой и газообразной, называется эта температура «тройной точкой») до 273,16 К (тройная точка воды):
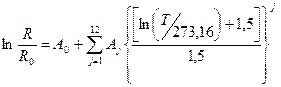 ;
;
- в области температур от 273,16 К до 1234,94 К (температура затвердевания серебра):
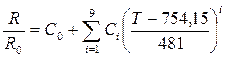 ,
,
где R – сопротивление ИП при температуре T;
R0 – сопротивление ИП при температуре 273,16 К;
А0, Аj, C0, Ci – постоянные коэффициенты, значения которых приведены в стандарте.
Потенциально высокая точность преобразования температуры в сопротивление может быть реализована только при условии преодоления некоторых недостатков подобных ИП.
В первую очередь, речь идет о низкой чувствительности α преобразователей. Предположим, с целью уменьшения инерционности и степени влияния на объект измерения (за счет высокой теплоемкости катушки с проволокой), вместо катушки взят один виток проволоки, длиной 1 см и площадью поперечного сечения 0,01 мм2. Сопротивление такого витка при 273,16 К будет равно R0 = 0,1 Ом. Изменение температуры на 1 К изменит сопротивление на α·R0 = 0,0004 Ом.
Поскольку терморезистивный ИП является параметрическим преобразователем, к нему необходимо по проводам подвести ток от внешнего источника питания и по другим проводам передать измерительный электрический сигнал последующему ИП. При этом оказывается, что на фоне колебаний сопротивлений подводящих проводов, помех, дрейфа нуля усилителей выделить сигнал, соответствующий изменению сопротивления ИП при изменении температуры на 1 К, практически невозможно.
Поэтому обычно низкую чувствительность компенсируют применением ИП с R0, равным 56, 100 или 500 Ом. Но увеличение числа витков проволоки ведет к росту ее массы и, как следствие, увеличению инерционности ИП и отбору им значительного количества тепла от объекта измерения.
Следующая сложность связана с тем, что терморезистор, в отличие от термопары, является параметрическим ИП; он не вырабатывает энергии – ее, как указывалось выше, нужно подавать от внешнего источника в виде электрического тока. Поскольку сопротивление ИП достаточно велико (а с ростом температуры при измерениях еще увеличивается), протекание тока сопровождается выделением джоулева тепла, повышающего температуру чувствительного элемента выше измеряемой.
Методы оценки влияния джоулева тепла на погрешность преобразования температуры в сопротивление и расчета допустимой величины питающего тока будут даны после рассмотрения тепловых полей; сейчас же можно указать, что величина тока не должна превышать единиц мА.
В заключение рассмотрения ИП температуры на основе терморезистивного эффекта, приведем данные по металлам, наиболее часто применяемых для изготовления промышленных и лабораторных термометров сопротивления [26].
Таблица 5.2.
Характеристики металлов для термометров сопротивления
| Металл | Диапазон преобразования, К | Чувствительность при 273К, К-1 | Примечания |
| Платина | 13 - 1300 | 0,004 | Высокая стабильность показаний, широкий диапазон преобразуемых температур; используются как в рабочих, так и эталонных ИП. |
| Медь | 70 - 473 | 0,004 | При температуре свыше 573 К активно окисляется, что определяет верхнюю границу диапазона преобразования. |
| Никель | 70 – 573 | 0,0064 | Высокая чувствительность и удельное сопротивление. Недостатки – сильное влияние примесей на функцию преобразования и структурное превращение при 623 К. |
5.6 ИП НА ОСНОВЕ ТЕНЗОРЕЗИСТИВНОГО ЭФФЕКТА
Суть эффекта, как указано в п. 5.3, состоит в том, что при растяжении или сжатии проволоки длиной l и поперечным сечением S в пределах упругой деформации, ее сопротивление изменяется. Малая величина упругой деформации определяет незначительность изменения сопротивления. А увеличение длины проволоки приведет к усреднению преобразуемой физической величины на большой длине, не обеспечивая преобразования локальных деформаций.
Преодолеваются возникшие противоречия использованием чувствительного элемента из тонкого провода (диаметром от 15 до 25 мкм) или фольги толщиной 3 – 5 мкм и специальной геометрической формой его укладки – зигзагом.
На рис. 5.4 показаны основные типы тензорезисторов. На тонкую подложку (порядка 0,03мм) из пластика напыляется металлическая фольга, которая потом травится по специальному фотошаблону; получившийся проводник называется решеткой. Поверх решетки приклеивается второй слой пластика. Слои пластика исключают возникновение электрического замыкания отдельных элементов решетки и предохраняют ее от механических повреждений. Концы решетки выводят для подключения внешних элементов и преобразователей (источников питания, измерительных усилителей). Подобным же образом изготавливаются и проволочные решетки.
 Тензопреобразователь приклеивается на поверхность детали так, чтобы проволоки решетки были направлены вдоль ожидаемых (или исследуемых) деформаций (на рис. 5.4 это вертикальное направление). Деформация поверхности детали приводит к деформации проволоки тензорезистора и изменению ее сопротивления.
Тензопреобразователь приклеивается на поверхность детали так, чтобы проволоки решетки были направлены вдоль ожидаемых (или исследуемых) деформаций (на рис. 5.4 это вертикальное направление). Деформация поверхности детали приводит к деформации проволоки тензорезистора и изменению ее сопротивления.
Применяться тензорезистор может как первичный ИП, если наклеить его на корпус двигателя, на элемент моста или плотины и т.д. В этом случае ИП преобразует в приращение омического сопротивления непосредственно измеряемую физическую величину – деформацию конструкции. А можно наклеивать (или напылять) решетку тензорезистора на мембрану, являющуюся первичным ИП давления; на стальной цилиндр преобразователя силы в деформацию и т.д. В этих случаях тензорезистор выполняет роль вторичного ИП.
Теперь рассмотрим вид функции преобразования тензорезистора.
Пренебрегая пока соединительными участками решетки, направленными поперек основного направления, можно, в соответствии с (5.12) и (5.13) записать выражение для сопротивления тензорезистора R:
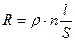 , (5.19)
, (5.19)
где ρ – удельное сопротивление проводника решетки;
n – число нитей в решетке;
l – длина одной нити;
S – площадь поперечного сечения нити.
Для определения величины относительного приращения сопротивления преобразователя ΔR/R, используем прием, описанный в гл. 3: выражение (5.19) прологарифмируем, потом продифференцируем по l, S, ρ и перейдем от дифференциалов к конечным приращениям. В итоге получим:
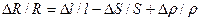 . (5.20)
. (5.20)
Далее необходимо относительные приращения площади и удельного сопротивления выразить через относительное приращение длины.
Начнем с площади поперечного сечения. По определению, при прямоугольном сечении провода площадь S = h·a, где h – высота, а – ширина проводника (для круглого провода S = π·d2/4, где d – диаметр). Логарифмируя выражение площади, беря производные и переходя к конечным приращениям, получим
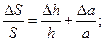

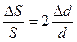 .
.
Согласно (5.2) относительная поперечная деформация связана с относительной продольной деформацией коэффициентом Пуассона, следовательно
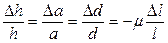 ,
,
и относительное приращение площади поперечного сечения проводника во всех случаях равно
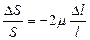 . (5.21)
. (5.21)
Перейдем к определению относительного приращения удельного сопротивления. Эта величина, как показали исследования, пропорциональна относительному изменению объема проволоки (формула Бриджмена [12])
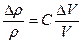 , (5.22)
, (5.22)
где С – константа Бриджмена;
ΔV/V – относительное изменение объема проводника.
Поскольку полный объем проводника равен V = S·n·l, то, с учетом (5.21)
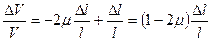 ,
,
и относительное приращение удельного сопротивления равно
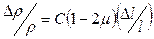 . (5.23)
. (5.23)
Подставив в выражение (5.20) значения соответствующих относительных величин из (5.21) и (5.23), после очевидных преобразований получим
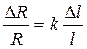 , (5.24)
, (5.24)
где константа k – чувствительность функции преобразования, равная
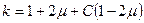 .
.
Эксперименты по определению константы С показали, что для металлов она близка к 1, поэтому можно принять значение чувствительности ИП k ≈ 2. Это дает основание представить, в первом приближении, функцию преобразования тензорезистивного ИП (5.24) в более простом виде
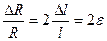 . (5.25)
. (5.25)
Величина относительного удлинения Δl ⁄ l = ε определяется из выражения (5.1) по известным механическим параметрам объекта (геометрическим размерам, модулю упругости и т.д.), к которому прикреплен тензорезистор.
Серийные тензорезисторы имеют стандартизованные значения сопротивлений в ненагруженном состоянии в диапазоне от 100 до 5000 Ом, величины относительных удлинений в пределах закона Гука приводились выше.
Можно убедиться, подставив в (5.25) приведенные в п. 5.2 величины относительных удлинений металлов в пределах упругости, что приращение сопротивления тензометра под нагрузкой составит весьма незначительную величину: максимальное относительное приращение сопротивления находится в пределах 0,002 – 0,01. Это усложняет последующее преобразование измерительного сигнала тензометра; решению возникшего затруднения будет посвящен п. 5.7.
А пока рассмотрим влияние на функцию преобразования тензометра поперечных участков проводника, соединяющих нити решетки. Указанные участки являются источниками одной из составляющих погрешности ИП.
Если полное сопротивление поперечных участков обозначить через RП, то сопротивление тензометра в ненагруженном состоянии будет 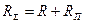 . При наличии поперечных деформаций детали, на которой укреплен тензометр, указанные участки решетки так же деформируются, и полное относительное приращение сопротивления имеет вид:
. При наличии поперечных деформаций детали, на которой укреплен тензометр, указанные участки решетки так же деформируются, и полное относительное приращение сопротивления имеет вид:
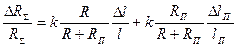 ,
,
где ΔlП / lП – относительное приращение длины поперечных участков проводника.
Первое слагаемое правой части содержит в знаменателе величину поперечного сопротивления, что указывает на снижение реальной чувствительности ИП относительно расчетного значения по (5.24), а второе слагаемое описывает вносимую аддитивную составляющую погрешности.
Парировать возникающие погрешности можно снижением сопротивления поперечных участков проводника так, чтобы обеспечить условие RП « R. Конструктивно этого добиваются, делая поперечные участки решетки много короче продольных и шире продольных, что хорошо видно на рис. 5.4а.
5.7. СХЕМЫ ПОДКЛЮЧЕНИЯ ПАРАМЕТРИЧЕСКИХ ИП
Поскольку параметрические ИП (терморезистивные и тензорезистивные преобразователи) не вырабатывают энергию, их подключение к последующим ИП связано с определенными сложностями. Основные требования, которые необходимо обеспечить при подключении параметрических преобразователей к источнику питания и последующему ИП следующие:
- не вносить существенных дополнительных погрешностей в результат преобразования первичным ИП (в выходной сигнал преобразователя);
- стремиться сохранить линейность функции преобразования дополнительных схем;
- обеспечить возможно большую чувствительность преобразования;
- парировать влияние внешних факторов (температуры, в первую очередь; изменений сопротивлений подводящих и отходящих линий и т.д.).
Для конкретизации дальнейшего анализа, будем рассматривать случай подключения тензометра; полученные результаты будут в полной мере распространяться на термометры сопротивления.
5.7.1. Потенциометрическое подключение ИП
Чтобы получить сигнал с тензорезисторного преобразователя необходимо пропустить через него ток от источника электрического напряжения. Тогда на сопротивлении тензорезистора R +ΔR возникнет падение напряжения по закону Ома. Как правило, источники электропитания имеют малое внутреннее сопротивление, и изменение сопротивления нагрузки не отражается на величине падения напряжения на нем. Другими словами, изменение сопротивления тензометра несколько изменит величину протекающего через него тока при неизменном падении напряжения на нем.
 Чтобы значимо изменялось напряжение на тензометре, последовательно с ним необходимо включить дополнительное (балластное) сопротивление. Упрощенная структурная схема включения тензометрического ИП представлена на рис. 5.5
Чтобы значимо изменялось напряжение на тензометре, последовательно с ним необходимо включить дополнительное (балластное) сопротивление. Упрощенная структурная схема включения тензометрического ИП представлена на рис. 5.5
К тензорезистивному ИП с сопротивлением RП подключен источник постоянного тока с напряжением е.
Ток, как видно на схеме, протекает последовательно через сопротивление R1, под которым понимается реальный резистор плюс внутреннее сопротивление источника питания и сопротивление подводящих проводов.
Нагрузкой ИП является входное сопротивление RВ следующего ИП. Для исключения влияния сопротивления проводов от тензорезистора до последующего ИП и замены ИП без дополнительной подстройки, обычно обеспечивают условие RВ » RП. Это условие позволяет исключить из рассмотрения влияние последующего ИП на функционирование тензопреобразователя.
При сделанном выше допущении, напряжение на тензорезисторе, по закону Ома, будет равно
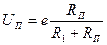 . (5.26)
. (5.26)
Полученное выражение может рассматриваться как функция преобразования нового ИП, включающего в себя тензорезистор как составную часть. Для оценки относительной погрешности преобразования, как и ранее, прологарифмируем (5.26), продифференцируем и перейдем к конечным приращениям:
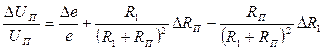 . ( 5.27)
. ( 5.27)
Обычно сопротивление R1 берется равным величине сопротивления ненагруженного тензорезистора, т. е. RП = R1 (причина этого будет понятна из дальнейшего анализа). Кроме того, неопределенность направления изменения погрешностей каждой составляющей в правой части (5.27), позволяет просуммировать все составляющие по модулю, что будет соответствовать случаю максимальной погрешности. С учетом сказанного, последнее выражение можно записать в виде:
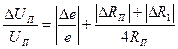 . (5.28)
. (5.28)
Проанализируем полученный результат.
Во – первых, правая часть выражения показывает, что нестабильности напряжения источника электрического питания е и величины обобщенного сопротивления R1 приводят к дополнительным погрешностям преобразования. Отсюда вывод - источник электропитания и сопротивление R1 необходимо рассматривать как измерительные преобразователи, чьи метрологические характеристики должны нормироваться и экспериментально исследоваться. Или придется поискать другое техническое решение, парирующее погрешность от нестабильности источника питания и сопротивлений.
Во – вторых, малый диапазон изменения сопротивления тензорезистора по сравнению с полным его сопротивлением, приводит к большой погрешностью преобразования при малых относительных изменениях полного сопротивления тензометра от влияющих величин. Если применить рассматриваемую потенциометрическую схему включения, то придется провести большое количество экспериментальных исследований принятых конструктивных решений и использовать сложные расчетные модели ИП.
Для пояснения сказанного, рассмотрим следующий типичный пример. Прогиб балки моста измеряется системой, первичным ИП которого служит тензометр с сопротивлением R0 = 500 Ом. Предельное относительное удлинение балки (в пределах упругой деформации) ε = 0,003. Согласно (5.25), изменение сопротивления тензометра во всем диапазоне удлинений составит 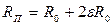 , т.е. весь диапазон изменения RП будет от 500 до 503 Ом.
, т.е. весь диапазон изменения RП будет от 500 до 503 Ом.
Пусть изменение обобщенного сопротивления R1 и самого тензорезистора от действия окружающей температуры незначительно, например, составляет 0,001 долю начального значения, или в абсолютных величинах в сумме 1 Ом. Относительно полного сопротивления тензорезистора (500 Ом) величина достаточно малая, но от изменяемой его части (максимум 3 Ома), несущей информацию об измеряемой физической величине, составит 30 % и более. Получается, что относительное изменение полного сопротивления потенциометрического ИП на 0,1% от действия влияющих факторов ведет к 30% относительной погрешности преобразования.
Здесь проявилась характерная особенность параметрических ИП: приращение изменяемого параметра под действием измеряемой величины составляет часть (часто незначительную) всего параметра, а приращение измерительного сигнала от влияющих факторов определяется всей величиной параметра.
Преодоление указанного недостатка является обычно сложной научно – технической и конструкторской задачей; для частного случая резистивных параметрических ИП решение будет приведено в следующем пункте.
Теперь вернемся к выражению (5.26) и определим приращение напряжения ΔUП при изменении сопротивления терморезистора под действием измеряемой величины на ΔRП:
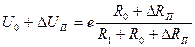 , (5.29)
, (5.29)
где U0 – падение напряжения на сопротивлении R0 тензорезистора в ненагруженном состоянии;
ΔRП = 2·ε·R0 – приращение сопротивления тензорезистора под нагрузкой.
Выходным параметром преобразователя является приращение напряжения ΔUП; для его определения вычтем из (5.27) выражение (5.26):
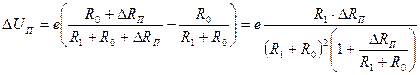 .
.
Поскольку в знаменатель последнего выражения входит значение приращения сопротивления тензорезистора ΔRП, то функция преобразования имеет нелинейный характер. Если считать, что для тензопреобразователей выполняется условие ΔRП « R1 + R0, функция преобразования приобретает линейный вид:
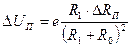 ,
,
и чувствительность преобразования S будет постоянной величиной, равной
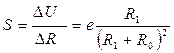 . (5.30)
. (5.30)
Теперь можно поставить следующий вопрос: при каком значении балластного сопротивления R1 будет иметь место максимальная чувствительность? Для ответа достаточно продифференцировать выражение (5.30) и приравнять результат к нулю:
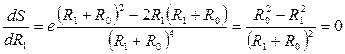 .
.
Откуда: максимум чувствительности преобразователя имеет место при R1 = R0 и равен он
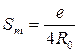 . (5.31)
. (5.31)
Дальнейший анализ потенциометрической схемы проводить не будем, поскольку она имеет один неустранимый существенный недостаток: присутствие в выходном сигнале UП = U0 + ΔUП большой неинформативной составляющей U0. Если вернуться к рассмотренному выше в данном разделе примеру и принять напряжение питания е = 10В, то U0 = 5 В, а значение информативного приращения сигнала не превысит ΔUПm = 0,03 В.
При этом необходимо помнить, что разделение напряжений сигнала мы делаем мысленно, используя принятую модель преобразователя. Физически же на выходе потенциометрической схемы с тензорезистором имеет место напряжение от 5,00 В до 5,03 В и отделить и усилить информативную часть сигнала в рассматриваемой схеме не представляется возможным.
Поэтому, как правило, в реальных измерительных системах используется мостовая схема включения, которую мы далее кратко рассмотрим.
5.7.2. Мостовые схемы включения параметрических ИП
Мостовые схемы являются частным случаем реализации дифференциального метода измерения, суть которого сводится к следующему:
Пусть имеется некоторая физическая величина X подлежащая измерению и известно априорно (до опыта), что измеряемая величина не принимает значений меньше Xmin. Тогда подбирают образцовую величину того же рода X0 из условия Xmin - X0 ≥ 0. Образцовой называется величина, значение которой известно с погрешностью намного меньшей (обычно от 3 до 10 раз), чем погрешности используемых средств измерений.
Далее реализуют процедуру физического вычитания X - X0 и дальнейшему измерительному преобразованию подвергают только остаток от вычитания ΔX = X - X0. Пример такого решения мы видели в главе 3 при рассмотрении схемы парирования дрейфа операционных усилителей.
Поскольку погрешностью образцовой величины X0, в силу ее малости, можно пренебречь, то погрешность результата преобразования будет определяться только погрешностью преобразования разности физических величин ΔX. Целесообразно выбирать величину X0 равной Xmin; в этом случае ΔX будет соответствовать изменяемой части физической величины.
Для резистивных параметрических преобразователей, у которых выходным сигналом является напряжение UП = U0 + ΔUП, за образцовую величину X0 принимают напряжение U0. Физическая реализация образцового напряжения U0 заключается в использовании второй потенциометрической схемы, подключенной к тому же источнику электрического тока, что и схема, рассмотренная в предыдущем пункте (рис. 5.6, делитель напряжения на сопротивлениях R2, R3). Каждое отдельное сопротивление в мостовой схеме называется плечом моста.
Источник питания е и сопротивления R1, RП образуют потенциометрическую схему, рассмотренную в предыдущем пункте, а сопротивления R2, R3 - вторую потенциометрическую схему.
Будем считать, как и в предыдущем пункте, что входное сопротивление последующего ИП очень велико и не оказывает влияния на работу мостовой схемы. Сделанное предположение вполне правдоподобно, поскольку входные сопротивления операционных усилителей (см. гл. 3) составляют сотни МОм, а сопротивления мостовых схем не превышают 1 - 5 кОм.
 При ненагруженном тензорезисторе, т.е. при RП = R0, напряжение точки А (рис. 5.6) относительно нижнего провода равно неинформативной части напряжения на тензорезисторе, то есть, U0. Согласно дифференциальному методу, желательно иметь напряжение точки В (образцовое напряжение) тоже равным U0. Условие баланса моста (равенства напряжений в точках А и В) может быть записано, если применить закон Ома. Падение напряжения на сопротивлении тензорезистора RП = R0 (обозначим его UА0) равно току по цепи R1 + R0, умноженному на сопротивление R0:
При ненагруженном тензорезисторе, т.е. при RП = R0, напряжение точки А (рис. 5.6) относительно нижнего провода равно неинформативной части напряжения на тензорезисторе, то есть, U0. Согласно дифференциальному методу, желательно иметь напряжение точки В (образцовое напряжение) тоже равным U0. Условие баланса моста (равенства напряжений в точках А и В) может быть записано, если применить закон Ома. Падение напряжения на сопротивлении тензорезистора RП = R0 (обозначим его UА0) равно току по цепи R1 + R0, умноженному на сопротивление R0:
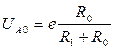 ; (5.32)
; (5.32)
аналогично падение напряжения на сопротивлении R3 (обозначим его UВ) равно

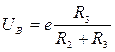 . (5.33)
. (5.33)
Приравнивая выражения (5.32) и (5.33)
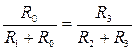 , (5.34)
, (5.34)
после простых преобразований получаем условие выполнения первого требования дифференциального метода измерений (условие равенства образцовой величины минимальному значению преобразуемого параметра):
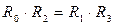 . (5.35)
. (5.35)
Второе требование дифференциального метода (вычитание физических величин) реализуется, если выходной сигнал снимать как разность потенциалов точек А и В, т.е. просто измерять напряжение между точками А и В. В этом случае, согласно (4.17),
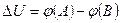 ,
,
или, измеряя потенциалы точек от одной базы (нижнего провода схемы), можно утверждать, что выходное напряжение мостовой схемы Um равно
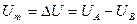 .
.
Если сопротивление тензометра изменяет свое значение под нагрузкой, напряжение точки А будет, в общем случае, изменяться как функция приращения сопротивления ΔRП
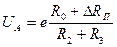 ,
,
и выходное напряжение мостовой схемы будет описываться следующим выражением, которое можно трактовать как функцию преобразования очередного ИП:
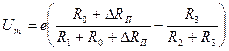 . (5.36)
. (5.36)
Второе слагаемое в правой части выражения заменим равным ему выражением из (5.34)
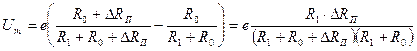 . (5.37)
. (5.37)
В последнем выражении, являющемся функцией преобразования мостовой схемы, нет в числителе отдельного слагаемого, определяемого начальным сопротивлением тензометра R0. Следовательно, выходное напряжение Um является функцией только приращения сопротивления ΔRП. Таким образом, поставленная цель исключить неинформативную часть сигнала, достигнута.
Максимальная чувствительность преобразования, как показано в п. 5.7.1, имеет место при условии R1 = R0; приняв это условие, последнее выражение можно упростить
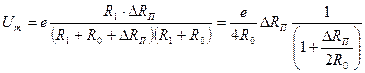 .
.
Сравнивая полученный результат с (5.29), заключаем, что максимальная чувствительность мостовой схемы близка к чувствительности потенциометрической схемы. Если приращение тензорезистора мало по сравнению с начальным значением, то последний сомножитель в правой части выражения близок к единице и функция преобразования становится линейной.
В заключение рассмотрим еще одно исключительно полезное свойство мостовой схемы. Для этого вернемся к выражению (5.34), предположив, что все сопротивления моста равны в исходном состоянии и что все они могут получать приращение, т.е. примем: RП = R0 + ΔR; R1 = R0 + ΔR1; R2 = R0 + ΔR2; R3 = R0 + ΔR3. При сделанных предположениях выражение (5. 34) примет вид
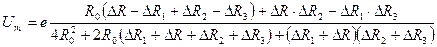 .
.
При малых значениях приращений их произведениями в числителе выражения, как величинами второго порядка малости можно пренебречь; так же поступим со всеми слагаемыми в знаменателе по сравнению с величиной 4 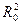 . В итоге получится следующее выражение для выходного сигнала мостовой схемы
. В итоге получится следующее выражение для выходного сигнала мостовой схемы
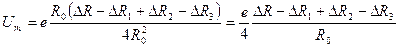 . (5.38)
. (5.38)
Вывод из последнего выражения: если в положении равновесия сопротивления всех плеч моста равны и приращения сопротивлений в смежных плечах равны, то разбаланса моста не наступает. А это позволяет парировать влияние внешних факторов на погрешность преобразователя (под ИП понимается, естественно, мостовая схема, частью которой является тензометр).
Практическую реализацию идеи покажем на примере измерения прогиба балки из п. 5.7.1. На балку наклеиваем 4 одинаковых тензорезистора: два из них по оси прогиба (они будут удлиняться по мере нагрузки моста), а два – поперек оси (на них действовать растягивающие усилия не будут).
Включим тензорезисторы в мостовую схему так, чтобы первые два образовали плечи RП и R2, а два вторых – соответственно плечи R1 и R3. На все 4 сопротивления действует внешняя температура, вызывая равное приращение сопротивлений (как в терморезистор
Дата добавления: 2015-04-29; просмотров: 1150;
