ПРЕОБРАЗОВАТЕЛЕЙ

2.1. ОБОБЩЕННАЯ ФУНКЦИОНАЛЬНАЯ СХЕМА ИП

В общем виде ИП представляет собой техническое устройство, имеющее входы (один или несколько), и выход. На вход подобного устройства поступает совокупность физических величин, характеризующих изучаемый физический объект, например, на вход амперметра поступает электрический ток, характеризуемый его формой, частотой, напряжением, фазовым сдвигом между током и напряжением, мощностью и т.д. Потребителя информации интересует одна из величин X, в частности, величина тока. В общем случае подлежащая определению физическая величина X изменяется во времени, т.е. Х = Х(t), где t - момент времени от какого-то условного начала отсчета (начала эксперимента, календарного года и тому подобного).

Поскольку физические объекты обладают совокупностью физических величин, на вход ИП поступают кроме Х(t) и те величины, которые не подлежат измерению 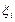(в нашем примере это напряжение, форма тока, частота, и т.д.); они называются неинформативными параметрами входного сигнала. Кроме того, на ИП воздействуют факторы окружающей среды, изменяющие, часто существенно, свойства преобразователя. Указанные факторы называются влияющими величинами и их значения обозначаются так же 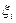. Сам измерительный преобразователь взаимодействует с измеряемым физическим объектом (например, потребляет от объекта измерений часть мощности), изменяя значение измеряемой величины Х(t); обозначим результат взаимодействия через N.

При создании ИП предполагалось, что он будет выполнять некоторое точно известное преобразование входной величины Х(t) в выходную величину Y_Н (t) по выбранной функции f_Н, называемой номинальной функцией преобразования. При отсутствии влияния ИП на объект измерения (т.е при N = 0) и постоянных, заранее оговоренных в документации значениях влияющих величин и неинформативных параметров входного сигнала 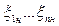(указанные условия называются нормальными условиями) :

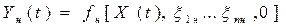. (2.1)

Очевидно, что функция преобразования должна обеспечивать однозначную зависимость выходной величины преобразователя от входной: увеличение или уменьшение значения входной величины X должно вести к соответствующему увеличению (или уменьшению) значения выходной величины Y. Желательно технически реализовать функцию, имеющую простое математическое описание и обеспечивающую возможно простую зависимость выходной величины от входной.

Всем указанным требованиям в максимальной степени отвечает линейная функция Y = SX + Y₀. Для ее описания достаточно двух параметров: начального значения выходной величины Y₀ (нулевого уровня), соответствующего нулевому (или какому-либо другому характерному) значению входной величины X, и показателя относительного наклона характеристики S = dY/dX, называемого чувствительностью преобразователя.

Чувствительность преобразователя – это, как правило, именованная величина с размерностью равной отношению размерности выходной величины Y к размерности входной величины X. Например, обычный ртутный термометр, в котором температура преобразуется в длину столбика ртути в капилляре, имеет размерность чувствительности м/⁰С, а термоэлектрический термометр, у которого выходным параметром является электрическое напряжение, соответственно В/⁰С.

На практике, к сожалению, чаще всего не удается найти такое преобразование входной величины X(t), чтобы на выходе ИП сигнал Y = f(X) был строго пропорционален величине входного воздействия. Например, преобразование давления в частоту вибрационно-частотного ИП происходит по уравнению, в котором входная величина стоит под знаком квадратного корня; уравнение преобразования криогенной температуры в сопротивление платинового термометра описывается уравнением двенадцатой степени и т.д. Как следствие - чувствительность преобразования S = dY/dX не остается постоянной по диапазону входной величины.

Преобразователь в реальных условиях применения (называемых рабочими условиями измерений) всегда имеет некоторые отличия от идеальной модели ИП:

· Функция преобразования f несколько отличается от теоретической модели f_н.

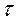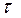· Выходной сигнал Y(t) преобразователя в момент времени t соответствует входной величине X в момент времени t - , где - время реакции преобразователя.

· Значения неинформативных параметров входного сигнала и влияющих величин x_i не совпадают с номинальными значениями x_iн.

· Влияние ИП на объект измерения N отличен от нуля.

По указанным причинам результат преобразования Y(t) в момент времени t имеет вид

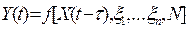. (2.2)

Разность выражений (2.2) и (2.1) определяет погрешность преобразования DU(t) значения физической величины Х(t). Естественно, на практике стремятся добиться того, чтобы погрешность преобразования DU(t) была существенно меньше выходного сигнала преобразователя Y(t). Учитывая малость величины DU(t) по сравнению с Y(t), разложим выражение разности в ряд Тейлора и ограничимся первыми членами разложения. Получим приближенное значение погрешности преобразования в виде:

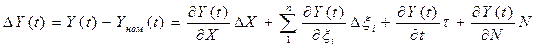, (2.3)

где 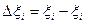_ном.

Необходимо сразу оговорить, что формула (2.3) не применяется для расчета погрешностей, а служит только для наглядного представления составляющих погрешности преобразования физической величины. Реальные погрешности имеют случайный (статистический) характер и их объединение производится по более сложным правилам математической статистики.

Рассмотрим отдельные члены правой части выражения (2.3). Первый называется основной погрешностью преобразователя - это погрешность, обусловленная не идеальностью собственных свойств ИП, т.е. отличием реальной характеристики преобразования f от номинальной f_н при нормальных условиях применения ИП. Второй член содержит дополнительные погрешности – погрешности результата преобразований, обусловленные реакцией преобразователя на изменения влияющих величин и неинформативных параметров входного сигнала относительно их номинальных значений. Третий член – динамическая погрешность – погрешность, обусловленная инерционностью ИП и скоростью изменения входного сигнала. Четвертый член содержит погрешность, которая образуется в результате взаимовлияния ИП на объект измерений (или на другой ИП, подключенный к входу или выходу анализируемого ИП). Особенность перечисленных групп погрешностей, кроме первой, состоит в том, что все они связаны не только со свойствами ИП, но и с условиями преобразования.

Смысл разбиения погрешности преобразования на различные составляющие заключается в том, что изучение каждой составляющей погрешности, уменьшение или исключение отдельных составляющих (это называется парированием погрешности) ведется разными способами и конструкторскими решениями.

Необходимо еще раз отметить, что непостоянство свойств самого ИП, скорости изменения измеряемой физической величины, неинформативных и влияющих параметров предполагают описание их моделей, в общем случае, понятиями и терминами математической статистики. В данном курсе не ставится задачи ознакомления студентов со статистическими моделями ИП. Указанный подход к анализу ИП будут изложен в других дисциплинах, после ознакомления с необходимым математическим аппаратом

2.2. АБСОЛЮТНАЯ, ОТНОСТИТЕЛЬНАЯ И ПРИВЕДЕННАЯ

ПОГРЕШНОСТИ ИП

Рассмотрим формы представления погрешностей преобразователей.

Предположим, что для некоторой физической величины, например, для биотоков мозга, предложен преобразователь с линейной (теоретически) функцией преобразования. Для нашего примера – это электронный усилитель постоянного тока с коэффициентом усиления 1000 и, следовательно, с номинальной функцией преобразования y = S·x = 1000ּx, где x, y – текущие значения входной и выходной физических величин, S – чувствительность. Это означает, что сигнал мозга в 0 мкВ должен преобразоваться усилителем в выходной сигнал 0 мкВ, а сигнал 20 мкВ - соответственно в 20000 мкВ.

Реальный преобразователь, в силу воздействия различных факторов (наводок, изменения напряжения питания, старения элементов схемы и т.д.), имеет несколько отличную от номинальной функцию преобразования. Как следствие, при подаче на вход усилителя 0 мкВ на выходе имеется сигнал 10мкВ; а при подаче на вход 20 мкВ, на выходе напряжение равно 20200 мкВ. Величина разности реального y_Р и номинального сигналов y_Н при каждом значении входного сигнала X называется абсолютной погрешностью преобразователя D_y, т.е. D_y = y_Р - y_Н. Величина D_y является объединением составляющих погрешностей, представленных в правой части выражения (2.3).

Графическая интерпретация сказанного дана на рис. 2.1; для наглядности картины, пропорции в изображении шкалы по оси Y искажены.

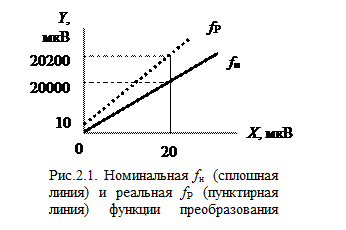Как видно из рисунка, абсолютная погрешность преобразования при входном сигнале x₁ = 0 равна D_y1 = 10 мкВ, а при сигнале x₂ = 20 мкВ - составляет D_y2 = 200 мкВ.

Абсолютную погрешность преобразования можно выразить по-другому, через входную физическую величину X. Для этого из номинального значения выходного сигнала (20000 мкВ) проведем горизонтальную линию до пересечения с реальной f_Р и номинальной f_н функциями. Из точек пересечения опустим перпендикуляры на ось X, которые дадут значения x_Р и x_н соответственно. Разность x_Р и x_н определяет значение абсолютной погрешности преобразования через входную величину, т.е. D_x = x_н - x_Р (обратите внимание на расстановку знаков при отсчете по оси X или Y).

Абсолютная погрешность не может, однако, служить мерой сравнения характеристик различных преобразователей. Действительно, абсолютная погрешность D_y = 200 мкВ составляет сотую долю от выходного сигнала 20000 мкВ, что может быть вполне приемлемо. А если те же D_y = 200 мкВ имеют место при выходном сигнале преобразователя 400 мкВ, то это никак нельзя считать допустимым. Поэтому вводится понятие относительной погрешности g_х = D_х/х = D_у/у, выражен­ной обычно в процентах.

Последнее понятие тоже не решает задачи оценки свойств ИП, поскольку при изменении значений х и у вдоль шкалы преобразователя, текущее значение относительной погрешности оказывается раз­личным для различных значений х: при больших значениях входной величины относительная погрешность мала, а при малых х относительная погрешность стремится к бесконечности. Вследствие этого в измерительной технике вводится еще одно специфическое понятие — приведенная погрешность, равная g₀ = D_х/Х_к = D_у/Y_к, где Х_к и Y_к - конечные значения диапазона измерения (если диапазон измерения начинается не с нуля, то Х_к и Y_к означают величину диапазона преобразования). По существу, g₀ является выраженной в процентах абсолютной погрешностью, так как в этом случае D_х (или D_у) относится не к текущему значению х, а к по­стоянной величине диапазона измерения Х_к (или Y_к).

2.3. АДДИТИВНЫЕ И МУЛЬТИПЛИКАТИВНЫЕ ПОГРЕШНОСТИ ИП

В теории ИП оказывается весьма важным разделение погрешности преобразования на составляющие в зависимости от изменения их значений при изменении входной величины x по диапазону преобразования.

Если реальная функция преобразования f_Р (на рис. 2.2,а обозначена цифрой 1) смещена относительно номиналь­ной 2 (рис. 2.2,а) так, что при всех значениях преобразуемой ве­личины x выходная величина у оказывается больше (или меньше) на одну и ту же величину D₀, то такая погрешность называется

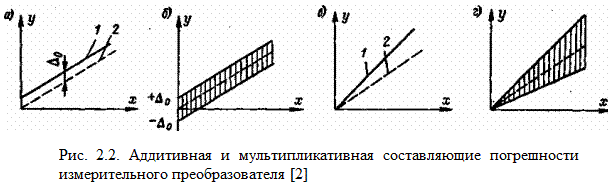аддитивной (по - латински «получаемая путем сложения») или погрешностью нуля. Если она является систематической, то есть постоянной по величине и неизменной во времени, то она может быть скорректирована путем смещения шкалы или смещения нулевого положения указателя. Для выполнения этой операции во многих приборах предусматривается электрическое или механическое устройство для установки нуля (так называемый «корректор»).

Если же аддитивная погрешность является случайной, то она не может быть скорректирована, и реальная характеристика, сме­щаясь произвольным образом (оставаясь параллельной самой себе), образует полосу погрешностей, ширина которой остается по­стоянной для любых значений х, как это показано на рис. 2.2, б.

Аддитивные погрешности возникают от постороннего груза на чашке весов при взвешивании, от неточной установки приборов на нуль перед измерением, от термо-э.д.с. в цепях постоянного тока и т. п.

Изменения чувствительности S преобразо­вателя (коэффициента усиления усилителя, коэффициента деления делителя, добавочного сопротивления вольтметра) ведут к тому, что абсолютная погрешность изменяется по диапазону преобразования и характеристика 1 преобразователя отклоняется от но­минальной 2 так, как это показано на рис. 2.2, в. Если отклонения являются слу­чайными, то они образуют полосу погрешностей (рис. 2.2, г).

Как видно из рисунка, возникающие вследствие этого абсолютные погрешности оказываются пропорциональными текущему значению преобразуемой величины x, и поэтому такая погрешность называется мультипликативной (по - латински «получае­мая путем умножения») или погрешностью чувстви­тельности.

Таким образом, погрешность преобразователя мы представили в виде двух компонентов: аддитивной (погрешность нуля) и мультипликативной (погрешность чувствительности). Возвращаясь к рассмотренному выше примеру, можно утверждать, что D_y1 = D₀ = 10 мкВ есть погрешность нуля данного усилителя (поскольку имеет место при нулевом значении входного сигнала). При входном сигнале x₂ = 20 мкВ погрешность складывается из погрешности нуля D₀ = 10 мкВ (еще раз подчеркиваем, что погрешность нуля постоянна во всем диапазоне изменения входной величины) и погрешности чувствительности D_y2S, равной D_y2S = D_y2 - D₀= 200 – 10 = 190 мкВ.

Создается впечатление, что аддитивная составляющая погрешности, неизменная во всем диапазоне преобразования, (в силу своей малости) несущественна по сравнению с мультипликативной составляющей, растущей вместе с входным сигналом. Поэтому аддитивной составляющей можно пренебречь, сосредоточившись на анализе и парировании мультипликативной погрешности.

Недопустимость подобного упрощения становится понятной, если рассмотреть относительные погрешности. Значения относительной аддитивной погрешности g(х) = D₀/x оказываются обратно пропорциональными х: при больших входных величинах х значения g(х) малы, но стремятся к бесконечности при приближении х к нулю. В этом заключается основное отрицательное свойство аддитивных погрешностей, не позволяющее использовать один и тот же пре­образователь для преобразования как больших, так и малых физических величин.

Чтобы относительная величина погрешности ИП не возрастала по мере уменьшения х, абсолютная погреш­ность преобразователя должна быть чисто мультипликативной. Тогда характеристика преобразователя, с учетом погрешности, описывалась бы выражением y = S(1 ± g_S)x, где gs — относительная погрешность изменения чувствительности. Абсолютная ширина полосы неопределенности в этом случае была бы пропорциональна преобразуемой величине х как d = 2g_S··x, а относительная погрешность g_S оставалась бы постоянной для любых малых значений х, ибо при х = 0 была бы равна нулю абсолютная погрешность преобразователя d.

Однако такой идеальный случай практически не осуществим, так как невозможно построить ИП, полностью ли­шенный аддитивных погрешностей. Эти погрешности в виде погрешностей от шума, дрейфа, трения, наводок, неизбежны в любых типах измерительных преобразователей. Поэтому у реальных ИП полоса неопределенности характеристики выглядит так, как это показано на рис. 2.1.

Функция преобразования реального ИП, с учетом аддитивной ±D₀, и мультипликативной ± g_S составляющих погрешностей, приобретает вид у = S(1 ± g_S) (х ± D₀). Производя умножение в правой части выражения и пренебрегая произведением двух малых величин g_S ·D₀, получим значение выходной величины в виде

у = Sх ± SD₀ ± Sg_S х. (2.4)

Выражение (2.4) отображает важное принципиальное свойство измерительных преобразователей – наличие погрешностей приводит к тому, что одному значению входной физической величины х могут соответствовать различные значения выходной величины у. Это значит, что величина у отображает входную величину х не одним значением, а в интервале погрешностей (с учетом возможных знаков перед составляющими погрешности) Dy = ±(SD₀+ Sg_S х).

2.4. ТРАНСФОРМАЦИЯ ПОГРЕШНОСТИ

ПОСЛЕДОВАТЕЛЬНОСТЬЮ ИП

При получении измерительной информации, как правило, выполняется не одно, а несколько измерительных преобразований; можно сказать, что ИП образуют последовательный измерительный канал. Каждый преобразователь в канале обладает собственными аддитивной и мультипликативной погрешностями. При этом возникают, по меньшей мере, два вопроса: во–первых, в какой форме представляется общая погрешность последовательно включенной группы ИП; и, во–вторых, как можно снизить общую погрешность последовательности ИП.

Из техники известны три возможных схемы включения преобразователей: последовательно, параллельно с последующим суммированием выходных сигналов и с обратной связью.

Рассмотрение начнем с последнего случая, когда часть сигнала с выхода преобразователя подается на вход для стабилизации параметров некоторого процесса. Классический пример подобного устройства – регулятор Уатта для стабилизации оборотов вала паровой машины. На вал паровой машины устанавливались подпружиненные эксцентрики, рычаг от которых соединялся с краном подачи пара в машину. При росте оборотов вала эксцентрики расходились, преодолевая силу пружины (или собственный вес эксцентриков) и через рычаг поворачивали кран в положение снижения подачи пара. При спаде оборотов вала (например, при увеличении нагрузки) процесс шел в обратном направлении, сильнее открывая кран подачи пара.

Говоря техническим языком, труба подачи рабочего тела (пара), машина и выходной вал охвачены цепью отрицательной обратной связи, в которую входят эксцентрики, пружина, рычаг и кран. Связь отрицательна по той причине, что часть энергии с выхода устройства (в нашем примере – паровой машины) подается на вход (на кран подачи) с обратным знаком: при росте оборотов сигнал в цепи обратной связи отрицательного знака (на уменьшение подачи пара); при уменьшении оборотов, т.е. при отрицательной производной от числа оборотов – подает сигнал опять с обратным знаком (на увеличение подачи пара).

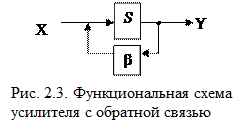Дальнейший анализ преобразователей предполагает введение математического выражения, связывающего входной и выходной сигналы цепи, охваченной отрицательной обратной связью. С указанной целью рассмотрим простейшую цепь: усилитель с коэффициентом усиления S (для линейного усилителя коэффициент усиления является его показателем чувствительности, введенным в п. 2.1) и отрицательную обратную связь с коэффициентом усиления β (рис 2.3). Поскольку речь идет о частичной передаче выходного сигнала на вход, то, очевидно, β ≤ 1.

Физически цепь обратной связи электронного усилителя может представлять собой резистивный делитель; для механического преобразователя – неравноплечный рычаг; для пневматического преобразователя – трубку с большим гидравлическим сопротивлением и т.д. Важно, чтобы в любом случае сигнал (воздействие) с выхода цепи обратной связи вычитался из входного сигнала X.

Сначала предположим, что линия с выхода цепи обратной связи разорвана. Тогда сигнал на выходе усилителя Y_ПР при входном сигнале х будет равен Y_ПР = Sּx. Подключим цепь обратной связи; сигнал на выходе изменится и примет неизвестное нам значение Y_ОС. Этот сигнал, пройдя цепь обратной связи станет равен βּY_ОС. Поскольку сигнал обратной связи вычитается из входного х, то на входе усилителя устанавливается значение сигнала х - βּY_ОС. Вот этот сигнал, усиленный в S раз, и создает выходной сигнал Y_ОС. Следовательно, можно записать следующее равенство:

Y_ОС = S(х - β·Y_ОС) = S· x - S· β·Y_ОС.

Произведя элементарные преобразования, получим окончательно

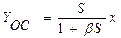. (2.5)

К каким же изменениям в преобразователе привело введение отрицательной обратной связи? Уменьшилась чувствительность преобразователя, она стала равна S_ОС = S/(1 + Sβ), и уменьшилась величина выходного сигнала (Y_ОС < Y поскольку знаменатель в (2.5) больше единицы).

Теперь, имея выражение для преобразователя с обратной связью, можно вернуться к задаче анализа погрешностей в канале преобразования измерительного сигнала.

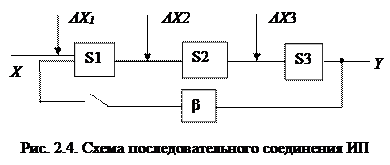Рассмотрим измерительную цепь, состоящую из нескольких преобразователей с известными характеристиками, например измерительную цепь, показанную на рис. 2.4, состоящую из трех последовательно включенных ИП с чувствительностью соответственно S₁, S₂, S₃, охваченных цепью отрицательной обратной связи с чувствительностью β.

Сначала, как и ранее, будем считать отрицательную обратную связь отключенной. Требуется найти показатели погрешности преобразования Y = f(X) в виде относительной погрешности чувствительности γ_S и погрешности нуля (дрейфа) ΔXо.

Для определения первой (мультипликативной) составляющей погрешности представим анализируемую измерительную цепь как сложный ИП, состоящий из трех последовательных звеньев, с крутизной статической характеристики (чувствительностью)

S = S₁S₂S₃. (2.6)

Выразим полный дифференциал S:

.

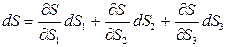Разделим обе части равенства на S и перейдем к конечным приращениям. Это дает приближенное развернутое выражение искомой относительной погрешности

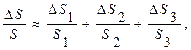
что означает: g_S = g_S1 + g_S2 + g_S3. (2.7)

(Вычисление относительной погрешности может выполняться более простым способом, основанном на том, что дифференциал от логарифма ln x равен d(ln x) = dx/x. Необходимо, следовательно, сначала прологарифмировать исходное выражение, продифференцировать результат и перейти от дифференциала к конечным приращениям. Например, логарифмируем выражение (2.6): lnS = lnS₁ + lnS₂ + lnS₃. Теперь дифференцируем и, переходя к конечным приращениям, сразу получаем: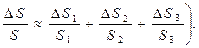

Для определения второй (аддитивной) составляющей погрешности DXо введем на вход каждого из трех элементарных ИП сигналы ΔX_i, где i = 1, 2, 3 (см. рис. 2.4), эквивалентные приведенным к входам значениям аддитивных погрешностей каждого звена. Затем трансформируем эти сигналы на вход измерительной цепи; их сумма даст

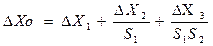. (2.8)

Выражения (2.6) и (2.7) показывают, что γ_S не зависит от порядка расположения элементарных ИП в измерительной цепи. А величина ΔХo, как видно из (2.8), зависит от порядка включения ИП: чем ближе к входу включен элементарный ИП, тем более жесткие требования надо предъявлять к нему по дрейфу нуля и помехоустойчивости. Например, если первый и второй преобразователи являются усилителями с номинальными коэффициентами усиления 10, то погрешность нуля первого преобразователя полностью войдет в результат преобразования, второго – только одна десятая часть, а третьего – вообще одна сотая.

Теперь включим в схеме обратную связь. Как показано выше, крутизна статической характеристики ИП с обратной связью S_{o c} равна

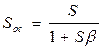, (2.9)

где β – коэффициент передачи цепи обратной связи.

Прологарифмировав (2.9), взяв производную и приведя подобные члены, придем к следующему выражению в конечных приращениях:

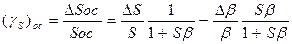; (2.10)

при условии βS » 1 полученное выражение упрощается

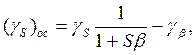
где γ_β = Δβ/β; g_S – из (2.7).

Из последнего уравнения видно, что относительная погрешность чувствительности обобщенного ИП с обратной связью определяется двумя слагаемыми. Если Sβ » 1, то первое слагаемое становится малым и, при достаточно хорошей стабильности звена обратной связи (т.е. малости слагаемого γ_β = Δβ/β), мультипликативная погрешность канала существенно понижается.

Как физически можно добиться выполнения условия Sβ » 1 при том, что β меньше единицы? Очевидно, для этого необходимо использовать усилитель в цепи прямой передачи сигнала с коэффициентом усиления S, стремящемся к бесконечности.

Обеспечить стабильность цепи обратной связи часто бывает проще, чем создавать высокостабильный ИП. Например, для измерительного усилителя цепь обратной связи может представлять собой делитель на резисторах, добиться стабильности которого неизмеримо проще, чем усилителя без обратной связи.

Становится понятным как можно понизить мультипликативную составляющую погрешности ИП – необходимо ввести отрицательную обратную связь; причем чувствительность цепи прямого преобразования S должна быть возможно большей.

Определим вторую составляющую погрешности в схеме с обратной связью, т.е. найдем выражение эквивалентного сигнала (ΔXo)ос, действующего на входе и вызывающего на выходе измерительной цепи такой же эффект, какой вызывают эквивалентные сигналы погрешности нуля ΔX₁, ΔX₂, ΔX₃.

На выходе измерительной цепи искомый эффект выражается уравнением

.

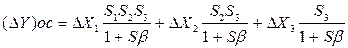Разделив обе части последнего выражения на чувствительность замкнутой измерительной цепи, получим:

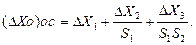(2.11)

Правые части (2.8) и (2.11) совпадают. Следовательно, обратная связь нисколько не изменяет величину аддитивной погрешности составного ИП.

Что же следует из проведенного анализа?

Во-первых, общая аддитивная погрешность последовательности ИП зависит от порядка подключения отдельных ИП, а мультипликативная – нет.

Во-вторых, мультипликативная погрешность может быть уменьшена введением отрицательной обратной связи, аддитивная погрешность – нет.

Главный вывод: при построении измерительного канала необходимо стремиться к тому, чтобы ИП имел тем меньшую аддитивную погрешность, чем он ближе подключен в канале к измеряемой физической величине.

Понятно, что наиболее жесткие требования предъявляются к первому в канале конструктивно обособленному ИП, который, повторим, называется датчиком. На датчик в максимальной степени действуют внешние дестабилизирующие факторы и неинформативные параметры измерительного сигнала (вибрации корпусов агрегатов; пульсации давлений и изменения температуры в измеряемой среде и окружающем пространстве, электромагнитные помехи и т.д.), сильно влияющие на погрешность преобразования. По указанным причинам разработка датчиков является для техники измерений наиболее сложной и актуальной задачей.

2.5. ДОПОЛНИТЕЛЬНАЯ ПОГРЕШНОСТЬ ИП

Дополнительная погрешность преобразования обусловлена, как указывалось в п. 2.1, реакцией ИП на изменения влияющих величин и неинформативных параметров входного сигнала относительно их номинальных значений. Дать полное описание указанной составляющей погрешности невозможно по нескольким причинам. Основные состоят в том, что состав влияющих факторов и неинформативных параметров индивидуален для каждого вида измерительного преобразователя, диапазона измерения и допустимой погрешности преобразования. Обычно для каждого типа ИП приводятся индивидуальные формулы, по которым можно рассчитать дополнительную погрешность от каждого вида влияющего фактора в конкретных условиях применения преобразователя.

Поскольку теоретически рассчитать влияние неинформативных параметров и влияющих величин более чем проблематично, то обычно для ИП технического применения (т.е. не для особо точных научных и метрологических работ) исходят из следующих предположений:

· погрешность от каждой влияющей величины не зависит от другой влияющей величины и значения полезного сигнала;

· погрешность линейно зависит от значения влияющей величины;

· общая погрешность от воздействия влияющих величин вычисляется по правилам объединения независимых случайных величин.

При принятых выше условиях экспериментально, на опытных образцах ИП, исследуют влияние каждого фактора отдельно и устанавливают выражения зависимости дополнительной погрешности от каждого из них.

Для примера рассмотрим измерение температуры платиновым проволочным термометром сопротивления с номинальным значением сопротивления равным 100 Ом при температуре 273,16 К (0⁰С).

Преобразователь представляет собой металлическую трубку, на конце который несколькими слоями намотана проволока из платины высокой очистки в лаковой изоляции. Концы катушки выводятся из трубки с тем, чтобы можно было подключить измеритель омического сопротивления. При нагреве (или охлаждении) проволоки ИП изменяется его сопротивление. В диапазоне температур примерно от жидкого азота (76 К) до 900 К функция преобразования имеет в первом приближении линейный вид: сопротивление датчика R зависит от температуры по закону

R = R₀ + S(T - T₀), (2.12)

где R₀ – сопротивление, соответствующее начальному значению температуры Т₀ диапазона измерения; приводятся в паспорте преобразователя;

Т – текущее значение измеряемой температуры;

S - чувствительность ИП, равная, в нашем случае, S = 0,4 Ом/К.

Далее необходимо к концам проволоки ИП присоединить, например, медными проводами, источник высокостабильного электрического тока. Тогда ток будет создавать на сопротивлении датчика падение напряжения по закону Ома, т.е. выполняется еще одно измерительное преобразование (сопротивления – в напряжение). Напряжение будем измерять вольтметром и по его показаниям судить о температуре объекта измерения.

Теперь все готово для получения информации о температуре какого-то объекта. Введем наш датчик в тепловой контакт с объектом. Сопротивление проволоки датчика увеличится, если объект имеет более высокую температуру относительно окружающей объект среды (или соответственно понизится при понижении температуры). На большем сопротивлении ток вызовет большее падение напряжения. Показания вольтметра делятся на известную величину тока питания ИП, и получается значение сопротивления датчика R в данный момент времени при данной температуре. Далее по выражению (2.12), зная R, вычисляется температура объекта T .

Приведенное выше описание преобразования температуры объекта в напряжение электрического тока является весьма грубой моделью действительных процессов. Для более детального анализа рассмотрим два случая: измерение высокой температуры (например, в трубопроводе подачи перегретого пара на турбину) и низкой температуры (жидкого водорода в трубопроводе горючего ракетного двигателя).

Первый случай. Поскольку температура в трубопроводе много выше температуры в окружающем пространстве, то по корпусу датчика и соединительным проводам происходит отток тепла. Платиновая проволока преобразователя имеет тепловой контакт и с корпусом датчика и с подводящими проводами, поэтому средняя температура (и, следовательно, сопротивление) будут меньше, чем действительная температура пара в точке нахождения преобразователя. Это первое. Во-вторых, протекающий через проволоку ток повышает внутреннюю энергию проволоки (по закону Джоуля), что приводит к росту ее температуры. В-третьих, высокая температура приводит к частичной диффузии изоляционного лака в проволоку и изменению ее функции преобразования. В-четвертых, перепад температур на проводах в местах подключения к платиновой проволоке медной приводит к появлению паразитной термо-э.д.с. (механизм ее появления будет объяснен в разделе, посвященном электропроводности металлов).

Второй случай. При низких температурах сохраняют влияние факторы теплопритока (только в этом случае сопротивление ИП оказывается завышенным), паразитной термо-э.д.с., прогрев джоулевым теплом. Но появляются и новые факторы. Отметим главные из них. Низкая температура ведет к уменьшению длины намотанной многослойной платиновой проволоки; как следствие - появление в ней внутренних механических напряжений, изменяющих функцию преобразования. Далее, температура жидкого водорода (порядка 20,3 К) ведет к уменьшению сопротивления ИП до 0,4 Ом, а чувствительность S ≤ 0,04 Ом/К. При столь малых сопротивлениях и чувствительности преобразователя начинают сильно сказываться сопротивления подводящих проводов. Ошибка в определении (или изменении) сопротивления линий в 0,01 Ом приводит к погрешности преобразования на 0,25 К, что для определения параметров ракетного топлива абсолютно недопустимо. Кроме того, на малом сопротивлении при постоянной величине тока выделяется низкое напряжение, с которым становятся сопоставимы шумы и электромагнитные наводки в подводящих проводах, искажающих действительные значения выходного сигнала датчика.

Рассмотренный пример показывает сложности, связанные с выявлением, изучением и учетом (или исключением) погрешностей от влияющих величин и неинформативных параметров физических величин. Этот процесс в технике измерения температуры проволочными термометрами сопротивления идет с 1871 г., когда их впервые применили, по настоящее время.

Для преобразователей других физических величин (как, впрочем, и для преобразователей температур на других физических эффектах) выявлению, анализу и парированию подлежат другие влияющие факторы. Часть из них можно предсказать из физических соображений, другая проявляется только при проведении экспериментальных исследований. При этом объем работ и ее сложность, как правило, превосходят разработку самого преобразователя.

2.6. ДИНАМИЧЕСКАЯ ПОГРЕШНОСТЬ ИП

Появление динамической погрешности обусловлено скоростью изменения измеряемой величины и инерционностью процесса ее преобразования в ИП. Очевидно, если величина долго не изменяется, то динамическая погрешность преобразования будет отсутствовать.

Продолжим пример предыдущего пункта с измерением температуры. Как преобразователь воспринимает измеряемую температуру? Допустим, исходная температура катушки с платиновой проволокой равна 300 К. Открывают задвижку и подают в трубу, в которой установлен наш преобразователь, пар с температурой 900 К. Пар омывает крайний слой проволоки и передает ей свою температуру. Сопротивление этого слоя проволоки вырастет, а остальных слоев останется прежним. Значение выходного параметра преобразователя (его сопротивление) в этот момент будет слабо отличаться от исходного, соответствовавшего температуре 300 К. Далее тепловой поток, проникая в более глубокие слои катушки, плавно увеличивает сопротивление ее витков, пока вся катушка не достигнет стационарной температуры 900 К. С этого момента выходной параметр ИП будет правильно отображать значение измеряемый физической величины (температуры пара).

Следовательно, с момента подачи пара и до полного прогрева преобразователя его выходной параметр с ошибкой отображал входную величину. Вот эта ошибка и называется динамической.

Предположим, при измерении температуры пара мы выяснили, что показания преобразователя стабилизировались через 0,5 с после начала подачи пара; далее можно считать, что динамическая погрешность преобразования отсутствует.

Теперь попытаемся с помощью нашего ИП измерить температуру горения смеси в цилиндре автомобильного двигателя. Цикл работы такого двигателя состоит из четырех этапов (всасывания, сжатия, горения смеси, выброса продуктов горения) одинаковой длительности, примерно по 1/400 доле секунды. Процесс горения еще короче, менее 0,001с. За такой промежуток времени катушка с проволокой преобразователя, помещенная в цилиндр двигателя, естественно, не успеет прогреться. Сопротивление провода (а, следовательно, в конечном итоге, измеренная температура) будет соответствовать некоторой средней температуре катушки провода ИП, которая на порядок ниже температуры горения смеси. Полученные результаты трудно назвать «измерительной информацией», поскольку они не отражают действительных значений измеряемой величины.

Инерционность характерна в той или иной мере всем преобразователям, отличие заключается только в механизме ее возникновения. Это может быть последовательная деформация слоев твердого вещества (например, при прогибе мембраны преобразователя давления), или волна местного уплотнения, перемещающаяся в газе или жидкости и т.д.

Каким же образом можно парировать динамическую составляющую погрешности? В технике измерений выработано несколько приемов. Во-первых, применение ИП на других принципах действия. Например, замена катушки преобразователя температуры на спай двух тонких проволочек (термоэлектрический преобразователь); замена механических элементов датчика давления (рычаги, шестеренки) нанесенной на мембрану тонкой проволокой в виде плоской фигуры (тензометрический преобразователь). Во-вторых, введение отрицательной обратной связи, рассмотренной ранее. В-третьих, ведение специальных корректирующих звеньев.

Мы не будем проводить детальный анализ динамической погрешности, поскольку количественное описание динамических характеристик ИП требует привлечения довольно сложного математического аппарата, а описание процессов прохождения сигнала через преобразователи еще сложнее. Заметим только одно. Без задержки не передается ни одно физическое воздействие, поскольку ни один носитель сигнала не может иметь скорость выше скорости света, а она конечна в любой среде.

2.7. ВЗАИМОДЕЙСТВИЕ ИП С ОБЪЕКТОМ ИЗМЕРЕНИЙ

2.7.1. Типы ИП и их особенности

В процессе измерения от физического объекта отбирается часть энергии, необходимая для преобразования ее в ИП в величину, удобную для последующего измерения или, что характерно для современных измерительных систем, удобную для передачи в пространстве с целью дальнейшего преобразования, обработки и отображения.

Измерительные преобразователи, рассматриваемые как преобразователи энергии, делятся на два типа (рис. 2.5):

- Генераторные ИП, которые дают энергию на выходе при одном энергетическом входе.

- Параметрические ИП, которые требуют двух и более энергетических входов для получения энергии на выходе. При этом основная (первичная) энергия Евх₁ поступает от измеряемой величины, а функция вспомогательной (вторичной) энергии Евх₂ заключается в том, чтобы перенести информацию, передаваемую основной энергией, на выход ИП.

В принципе, ИП могут быть построены с использованием восьми основных форм энергии: механической, гидравлической (акустической), термической, электрической, магнитной, оптической, химической, ядерной. В связи с этим теоретически может быть создано 8² = 64 типа генераторных и 8³ = 512 типов параметрических ИП. Однако в практике измерений реализовано лишь небольшое число возможных вариантов. Кроме того, у современных преобразователей выходной сигнал представлен в основном электрической формой, что сразу сокращает число комбинаций в 8 раз.

Генераторные ИП более просты по схеме и принципу действия, чем параметрические. В них для выполнения измерительного преобразования и формирования выходного сигнала ИП используется энергия измеряемой величины. В параметрических ИП измеряемая физическая величина изменяет какой-то параметр преобразователя при малых затратах энергии. А формирование выходного сигнала ИП обеспечивается энергией внешнего источника, не создавая энергетической нагрузки на исследуемый физический объект. Несмотря на относительную сложность, ИП такой конструкции обладают меньшими погрешностями преобразования и более высокой помехоустойчивостью и поэтому более распространены, чем генераторные.

Для пояснения различия между двумя типами преобразователей, рассмотрим следующий пример. Необходимо измерить давление газа в баллоне для газовой сварки (давление порядка 10⁷ Па) и давление остаточного газа в вакуумной камере для напыления микросхем (давление порядка 10^-7 Па).

Преобразовать давление газа в баллоне в механическое перемещение можно с помощью изогнутой и сплющенной по длине трубки, заваренной на одном конце (трубка Бурдона). При подаче в трубку газа через второй конец, трубка изгибается и заваренный конец перемещается. Если к нему прикрепить тяги и соединить со стрелкой на оси, то стрелка будет поворачиваться в функции от давления, т.е. давление будет преобразовано в угол поворота стрелки (рис. 2.6).

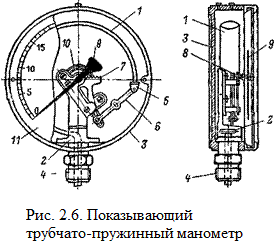Трубчатая пружина 1 открытым концом жестко соединена с держателем 2, укрепленным в круглом корпусе 3 манометра. Держатель несет на себе штуцер 4 с резьбой, служащий для сообщения прибора с измеряемой средой. Свободный конец пружины закрыт пробкой 5 с шарнирной осью и запаян. Посредством по­водка 6 он связан с передаточным механизмом, состоящим из зубчатого сектора 7, сцепленного с шестеренкой (трибкой) 8, сидящей неподвижно на оси вместе с указательной стрелкой 9. Рядом с трибкой расположена плоская спи­ральная пружинка (волосок) 10, один конец которой сое­динен с трибкой, а другой закреплен неподвижно на стойке, поддерживающей передаточный механизм. Воло­сок постоянно прижимает трибку к одной стороне зубцов сектора, благодаря чему при обратном изменении давления устраняется мертвый ход в зубчатом зацеплении передаточного механизма.

Под действием измеряемого давления трубчатая пру­жина (трубка Бурдона) частично раскручивается и тянет за собой поводок, приводящий в движение зубчато - секторный механизм и стрелку манометра, перемещающуюся вдоль шкалы 11. Манометр имеет равномерную круговую шкалу с центральным углом 270—300°.

Оценим силу, создаваемую газом при повороте стрелки. Примем, что трубка Бурдона имеет в поперечном сечении форму прямоугольника с длиной l = 6мм и шириной h = 2мм (внутренние размеры трубки). Трубка изогнута по дуге окружности в 270⁰ с радиусом по внутренней стенке R_V = 30 мм. Газ, поступивший в трубку из баллона, создает давление на стенки трубки. Поскольку площадь наружной стенки, удаленной от центра на радиус R_N = R_V + 2мм больше, чем стенки, удаленной от центра на радиус R_V, то возникает сила, стремящаяся разогнуть трубку. Эта сила равна

.

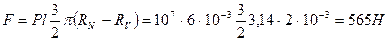Сила F преодолевает силы упругого сопротивления трубки и силы трения в узлах передачи перемещения от трубки до стрелки. Сила трения невелика и составляет примерно 0,001F, т.е. порядка 0,5 Н; по сравнению с величиной действующей силы потерями на трение можно пренебречь. Кроме того, объем трубки настолько меньше объема баллона, что его подключение к баллону заметно не изменяет давления газа в нем.

Теперь перейдем к измерению низкого давления, которое по условию равно Р = 1·10^-7 Па. Упростим расчет (нам важны не точные цифры, а порядок величин). Будем считать, что вместо трубки Бурдона используется мембрана с нулевой упругостью, не требующая силы на свой прогиб. У мембраны более эффективно используется площадь. С одной стороны мембраны – измеряемое давление, с другой – полость с еще более низким давлением, например, 1·10^-10 Па. К мембране прикреплен показывающий механизм от измерителя с трубкой Бурдона. Какова же должна быть площадь мембраны П, чтобы стрелка отклонялась от начального (нулевого) положения?

Поскольку по условию мембрана прогибается без усилия, то сила, развиваемая давлением газа должна только преодолеть трение механизма: 0,001F = P·П = 1·10^-7 П, где П - площадь мембраны. Откуда П = 5·10⁶ м². Получается, что площадь мембраны должна быть порядка 5 квадратных километров. Почему же получился такой результат? Потому, что для функционирования нашего генераторного преобразователя давления в угол поворота стрелки необходим большой запас энергии измеряемой физической величины (напоминаем, что давление есть мера потенциальной энергии газа). Совершенно очевидно, что прогиб мембраны указанной площади приведет к существенному изменению объема вакуумной камеры и результаты измерений будут далеки от действительного значения физической величины, несмотря на все затраченные усилия по выполнению измерительного преобразования.

Заменим генераторный преобразователь параметрическим. Например, на вакуумный диод. Устроен он следующим образом. К нагретой металлической нити, называемой катодом, подключают отрицательный полюс источника электрического питания. К металлической пластинке, называемой анодом, расположенной на некотором удалении от катода (порядка 10 мм), подключают положительный полюс источника питания.

Вокруг раскаленного катода образуется облако электронов, которое притягивается электростатическим полем к аноду и во внешней цепи должен возникнуть электрический ток. Однако, при высокой плотности газа (высоком давлении) ток между катодом и анодом равен нулю, поскольку электроны с катода соударяются на малой скорости с молекулами газа и, в итоге, направление их движения становится хаотическим, определяемым тепловым движением молекул газа. С понижением давления газа длина свободного пробега электронов возрастает, кинетическая энергия становится такой, что выбивает вторичные электроны из молекул газа. При этом электроны, под действием поля анод - катод движутся в сторону анода, а образовавшиеся положительные ионы – в сторону катода. Во внешней электрической цепи ток пропорционален степени разряжения, т.е. обратно пропорционален остаточному давлению.

Откуда в данном случае берется энергия преобразования? От внешнего электрического источника. Измеряемый параметр только изменяет проводимость среды в преобразователе. И объем подключаемого ИП того же порядка, что у трубки Бурдона, чем обеспечивается сохранение давления в объеме вакуумной камеры.

2.7.2. Энергетическое согласование ИП

Кроме вопроса выбора типа преобразователя, возникает вопрос эффективности использования энергии измеряемой физической величины или внешнего источника (для параметрических ИП). Задача формулируется следующим образом: каким должно быть соотношение между сопротивлениями источника сигнала и преобразователя для наиболее эффективной передачи энергии, несущей информацию об измеряемой физической величине.

Анализ оказывается различным для генераторных и параметрических преобразователей вследствие различного механизма передачи ими информации.

Рассмотрим генераторный преобразователь П₁ представленный своей э. д. с. Е(x) и своим неизменным внутренним активным сопротивлением R₁, а последующий за ним преобразова­тель П₂ представлен лишь своим входным активным сопротивлением Rн, являющимся нагрузкой для предыдущего преобразователя (рис. 2.7). В этом слу­чае мощность Рн, передаваемая от преобразователя П₁ к преобразователю П₂, равна Рн = I²Rн, где I — ток, проходящий между этими преобразователями.

Если напряжение Е и внутреннее сопротивление R₁ ИП считать заданными, а оптимизацию передачи энергии осуществлять выбором значений Rн, то очевидно, что ток I может изменяться лишь от нулевого значения при холос­том ходе Iхх = 0 при Rн = ¥, когда Pн = 0, до значения при коротком замыкании I_K3 = Е/R₁ при Rн = 0, когда вновь Рн = 0. Следовательно, максимум Рн находится при 0 < I < Е/R₁ и 0 < Rн < ¥.

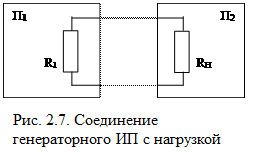Для установления условий этого максимума, учитывая, что ток равен I = E/(R₁ + R_н), запишем выражение для Р_Н как

.

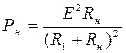Поскольку для нас представляет интерес соотношение между сопротивлением нагрузки R_Н и неизменным внутренним сопротивлением R₁, то введем параметр а = R_Н/R₁, отражающий это отношение. Вынеся в последнем выражении из знаменателя R₁ и заменив отношение сопротивлений R_Н/R₁ на параметр а, получим:

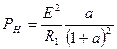. (2.13)

В выражении (2.13) первый сомножитель характеризует мощность источника информации, а второй - эффективность процесса преобразования.

Зависимость передаваемой мощности Р_Н от мощности источника информации линейна и здесь нечего анализировать: чем больше мощность источника, тем большая мощность может быть использована для преобразования измеряемой величины.

Для определения условия наиболее эффективного преобразования возьмем первую производную от второго сомножителя в (2.13) и приравняем ее нулю. В результате получается условие оптимизации: а = 1, т.е. R_Н = R₁. Другими словами, энергия генераторного преобразователя используется наиболее эффективно в информационном смысле при условии равенства внутреннего R₁ и нагрузочного R_Н сопротивлений.

Если при создании измерительного канала сильно отступить от условий оптимальности, то уменьшится мощность Рн, получаемая следующим преобразователем, и во столько же раз падает информационно-энерге­тический к. п. д. всего канала преобразования, т. е. понижается его чувствитель­ность, точность и рабочий диапазон. Для компенсации этих потерь приходится увеличивать мощность Ро, потребляемую от объекта измерения, снижать быстродействие, вводить в прибор усилители и т. д.

Соблюдение же условий согласования, обеспечивая максимум энергетического к.п.д. преобразования, не тре­бует материальных затрат, а достигается лишь оптимальным рас­четом узлов измерительных преобразователей. Поэтому согласование входных и выходных сопротивлений преобразователей широко ис­пользуется на практике.

Правило согласования отнюдь не тре­бует равенства R₁ и Rн с какой-либо высокой степенью точности. Практически согласование обеспечивается даже при а = 3…5, если это почему - либо удобнее для реализации.

Вывод условий согласования сопротивлений параметрических преобразователей значительно сложнее. Мы этого делать не будем, а приведем сразу результаты анализа.

Мощность сигнала на нагрузке возрастает с ростом мощности источника питания параметрического преобразователя и его чувствительности; максимум мощности на нагрузке Rн соответствует условию Rн = Ro/3.

В заключение необходимо подчеркнуть, что все выводы о согласовании сопротивлений делались в предположении постоянства сопротивлений источника, приемника информации и соединяющих их линий связи во всем диапазоне изменения измеряемой величины и внешних условий. Эти требования часто не выполняются. Поэтому оптимизация сопротивлений предполагает проведение предварительно соответствующих исследований преобразователей.

2.8. ИТОГИ РАССМОТРЕНИЯ ИЗМЕРИТЕЛЬНЫХ

ПРЕОБРАЗОВАТЕЛЕЙ

Всякое преобразование измерительной информации, как указывалось выше, связано с преобразованием и затратой энергии. При этом в устройствах преобразования должны реализовываться такие физические законы и эффекты, чтобы ИП отвечали комплексу весьма специфических требований.

Номенклатура требований обширна; обычно это требования по надежности и взрывозащите, климатические и габаритно - весовые ограничения, экономические и эксплуатационные требования и т.д. Все указанные параметры важны и должны учитываться при конкретной разработке ИП. Но в первую очередь необходимо использовать такие физические эффекты, которые обеспечат выполнение следующих требований:

- линейность функции преобразования;

- максимальную чувствительность;

- минимальную аддитивную составляющую погрешности;

- незначимость динамической составляющей погрешности;

- малую погрешность от воздействия влияющих на ИП факторов и неинформативных параметров физической величины;

- пренебрежимо малую погрешность от воздействия ИП на объект измерения.

Выполнить все перечисленные требования в одном устройстве, конечно, невозможно. Техническое проектирование всегда есть процесс поиска разумного компромисса. Например, для точного преобразования силы или давления в частоту электрического сигнала используют струнные преобразователи, обладающие нелинейной функцией преобразования. В примере с измерением температуры в цилиндре двигателя мы применили термоэлектрический преобразователь вместо более точного термометра сопротивления ради снижения динамической погрешности преобразования.

Еще сложнее решается вопрос обеспечения заданной погрешности преобразования. Как указывалось выше, уравнение (2.3) является иллюстративным и не пригодно для расчетов погрешности ИП. Связано это с тем, что их погрешности (основная, от влияющих факторов, динамическая и т.д.) являются случайными процессами. В общем случае величина каждой составляющей погрешности ИП и их взаимное влияние изменяются во времени случайным, непредсказуемым образом. Значительно труднее ответить на вопрос как преобразуются (трансформируются) случайные погрешности, пройдя через последовательную цепь ИП. Сказанное не означает, что ответов не поставленные вопросы нет. Ответы будут даны в курсах «Теории измерений» и «Теории, расчета и проектирования измерительных устройств».

Пока что можно констатировать только одно – чем меньше величина каждой составляющей погрешности ИП, тем меньше общая погрешность преобразования при любом методе объединения составляющих.

Задача специалиста сводится к разработке или применению ИП на таких физических эффектах, которые в процессе получения измерительной информации обеспечат заданное приближение результата измерения к действительному значению измеряемой физической величины при выполнении всех экономических, эксплуатационных и других ограничений.