Дифференциальные уравнения движения твердого тела
При поступательном движении твердого тела все его точки движутся также как центр масс. Поэтому поступательное движение тела сводится к движению любой его точки, и дифференциальными уравнениями поступательного движения будут являться проекции теоремы о движении центра масс на оси координат, где произвольной точкой будет центр масс.
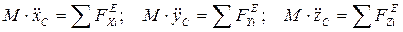 . (10.1)
. (10.1)
Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси имеет вид:

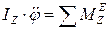 (10.2)
(10.2)
Произведение углового ускорения тела на осевой момент инерции равно сумме моментов внешних сил относительно оси вращения.
Дифференциальные уравнения плоского (плоскопараллельного) движения твердого тела может быть представлено как поступательное движение вместе с центром масс и вращательное движение вокруг оси ОZ:
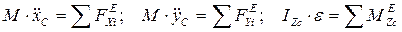 (10.3)
(10.3)
IZc –момент инерции тела относительно оси, перпендикулярной плоскости движения и проходящей через центр масс.
Дата добавления: 2015-04-29; просмотров: 2170;
