Теорема об изменении кинетического момента

Моментом количества движения материальной точки относительно центра О называется вектор

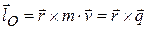, (9.1)

где 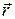– радиус-вектор материальной точки относительно точки O.

При движении точки в плоскости относительно некоторого центра О ее кинетический момент относительно данного центра может быть определен как алгебраическая величина следующим образом (поступательное движение):

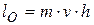, (9.2)

где h – кратчайшее расстояние между точкой O и вектором скорости .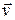

Главный момент количеств движения материальных точек механической системы относительно некоторого центра О является кинетическим моментом системы относительно данного центра О и определяется как:

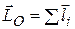. (9.3)

Кинетический момент твердого тела вращающегося вокруг неподвижной оси равен произведению момента инерции тела относительно оси вращения на его угловую скорость.

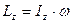. (9.4)

Теорема об изменении момента количества движения материальной точки имеет вид – производная по времени от момента количества движения материальной точки относительно некоторого центра О равна сумме моментов сил, действующих на точку относительно того же центра.

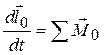. (9.5)

Теорема об изменении кинетического момента механической системы может быть выражена следующим образом

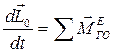. (9.6)

Производная по времени вектора кинетического момента системы относительно некоторого центра О равна главному моменту внешних сил, действующих на систему относительно того же центра.