Построение преобразователя двоично-десятичного кода в двоичный код
Двоичные числа, содержащие 4 или менее разрядов, преобразуются непосредственно, как 1 тетрада. Двоичные числа, имеющие длину более 4-х разрядов, можно преобразовать в двоично-десятичную форму с помощью сдвигающих регистров. Для этого двоичное число надо сдвигать справа налево старшими разрядами вперёд, записывая («вдвигая») его в регистр последовательно, разряд за разрядом, начиная с младшего разряда регистра. Сдвиги надо повторять до тех пор, пока младший разряд двоичного числа не запишется в младший разряд регистра, который можно рассматривать как двоично-десятичную разрядную сетку. Когда единица пересекает границу между двоично-десятичными разрядами, то возникает ошибка, так как при сдвиге значение этой единицы увеличивается с 8 до 16, тогда как для двоично-десятичного числа оно должно возрасти с 8 до 10. Следовательно, для коррекции тетрады необходимо добавлять цифру 6, так как двоично-десятичное число уменьшается на 6.
Таблица 6.4Таблица истинности преобразователя
двоично-десятичного кода в двоичный
| i | X4 | Хз | X2 | Xl | Y4 | Y3 | Y2 | Y1 |
Таблица 6.5Данные по коррекции сдвига двоично-десятичных чисел
| ДЧ | MP | ||||
| Вес | 103 | 102 | 101 | ||
| ДЦЧ | |||||
| с | |||||
| к | |||||
| ДДЧ | |||||
| ДЧ |
В таблице 6.5 приведены: ДЧ - десятичное число, ДЦЧ - двоично-десятичное число, С - сдвиг, К - коррекция, МР - младший разряд.
Если в старший разряд тетрады, имеющей множитель 10j, поступает единица, то она приобретает вес 8*10j. До сдвига эта единица имела вес 10i+1, поэтому для получения при сдвиге деления на два ей следует приписать вес 2-1*10j+1. Из этого следует, что необходимо произвести коррекцию на число 8*10j - 2-1*10j+1, т.е. вычесть число 3*10j. Если в старший разряд какой-либо тетрады поступает нуль, то коррекцию производить не нужно. Из таблицы видно, что после сдвига числа 9653 и соответствующей коррекции действительно получается число 4826, отличающееся от 9653*2-1 на единицу, которая является младшим разрядом младшей тетрады двоично-десятичного кода и младшим разрядом двоичного кода.
Если вы строите преобразователя двоично-десятичного кода в двоичный код на элементах И-НЕ, то рассуждения как и для предыдущего преобразователя. Получим схему:
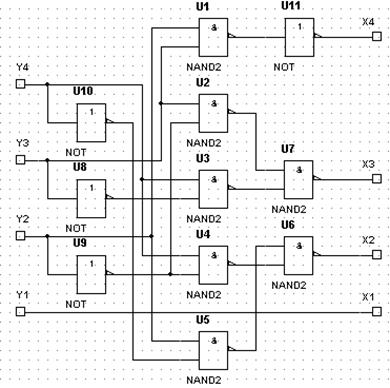
Рис. 6.32 Схема преобразователя двоично-десятичного кода в двоичный код
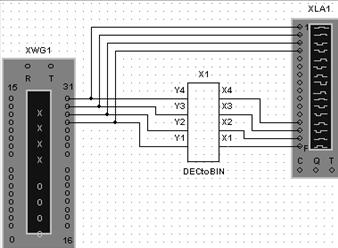
Рис. 6.33 Блок преобразователя двоично-десятичного кода в двоичный код
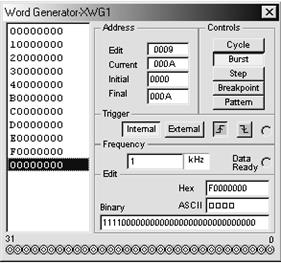
Рис. 6.34 Заданная последовательность входных сигналов
для схемы (рис. 6.18)
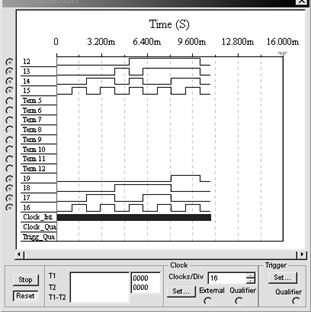
Рис. 6.35 Временные диаграммы для преобразователя двоично-десятичного кода в двоичный код
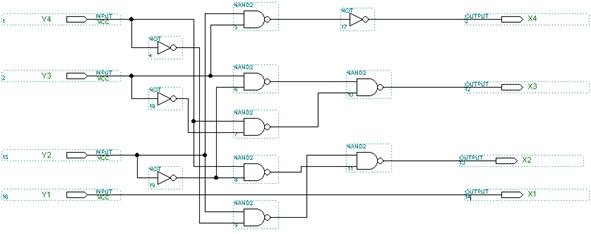
Рис. 6.36 Преобразователь двоично-десятичного кода в двоичный код
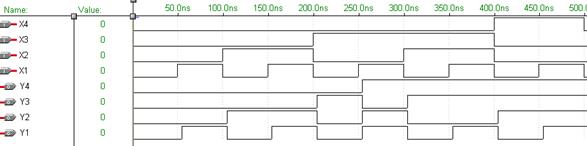
Рис. 6.36 Временные диаграммы
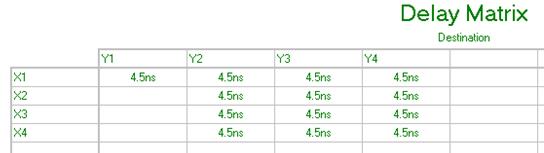
Рис. 6.37 Матрица временных задержек
Программа:
SUBDESIGN preobraz_dvoichno_desayt_v_dvoich
( X[3..0] : INPUT;
Y[3..0] : OUTPUT; )
BEGIN
IF X[3..0] <= B"0100"
THEN Y[3..0] = X[3..0];
ELSE
Y[0]=X[0];
TABLE
X[3..1] => Y[3..1]
B"101" => B"010";
B"110" => B"011";
B"111" => B"100";
END TABLE;
ENDIF;
END;
Дата добавления: 2015-04-25; просмотров: 2875;
