Взаимозаменяемость благ. Эффекты компенсации

Если функция спроса имеет вид 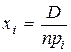(или, при неравных между собой 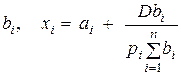), то спрос на i-й товар не зависит от цены на любой j-й товар.

Перекрестные функции спроса от цен характеризуют такие свойства товаров, как взаимозаменяемость и взаимодополняемость. Если при росте цены на товар i, при снижении спроса на i-й товар, растет спрос на j-й товар - эти товары взаимозаменяемы (например, картофель - крупы; чай - кофе). Наоборот, если спрос на j-й товар также падает, - они взаимодополняемы.

Заметим, что реальная взаимозаменяемость может искажаться общим снижением благосостояния при росте цены i-го блага: j -ое благо может заменять i-е в потреблении, но спрос на него может не расти, поскольку снизилось общее благосостояние потребителя.

Для снятия этого искажения используют понятие компенсированного изменения цены, то есть такого, которое сопровождается увеличением дохода потребителя, позволяющим ему поддерживать прежний уровень благосостояния. Практически компенсированное изменение цены изображается следующим образом (рис.10.2).

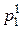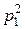Пусть цена первого блага повысилась c до тогда бюджетная прямая из положения 1 перейдет в положение 2. Точка А на линии безразличия 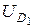, касающейся первоначального бюджетного ограничения, будет заменена новой точкой оптимума В, где новая линия безразличия 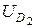, касается новой бюджетной прямой. Если мы хотим компенсировать потребителю потерю благосостояния, то увеличим его доход так, чтобы новая бюджетная прямая 3 (параллельная линии 2) коснулась в некоторой точке С прежней линии безразличия .

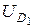Направленный отрезок АС показывает "эффект замены" при росте цены, то есть изменение структуры спроса при условии поддержания прежнего уровня благосостояния. Направленный отрезок СВ отражает "эффект дохода", то есть изменение потребительского спроса при сохранении соотношения цен благ и изменении уровня дохода. Общий результат роста цены (при отсутствии компенсации) выражается направленным отрезком АВ.

Для формального анализа компенсационных эффектов рассмотрим вначале две задачи.

Пример 10.1. Пусть целевая функция потребителя (ЦФП) зависит от двух благ 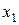и 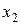следующим образом: 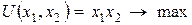. Пусть цены благ равны, соответственно, 10 и 2, а доход потребителя - 60. Тогда, согласно полученной формуле функции спроса, 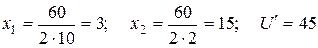. Пусть теперь р меняется с 2 до 7. Каков необходимый размер компенсации?

Чтобы приобрести прежний оптимальный набор, потребителю необходимо дополнительно (7 - 2) × 15 = 75 денежных единиц.

Однако прежняя структура потребления не будет оптимальной при новых ценах, и минимальная необходимая компенсация будет меньше, чем 75.

Пусть потребитель получает дополнительно количество денег М. Тогда при новых ценах его спрос на первое и второе блага будет равен:

.

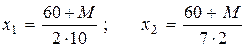Целевая функция 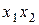будет равна 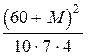, и это выражение должно равняться начальному 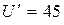. Отсюда , что существенно меньше, чем 75.

Теперь решим задачу в более общем виде. Пусть по-прежнему 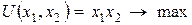; цены благ равны 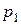, и 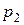, а доход 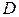. Очевидно, что

.

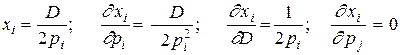Пусть теперь цена 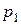выросла в К раз (К > 1), и при этом потребитель получает необходимую компенсацию. Новый размер дохода обозначим через 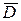, спрос- 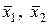. Очевидно, 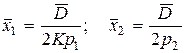и условие компенсации 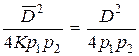, откуда .

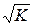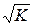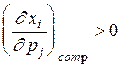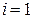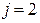Итак, спрос на первый товар в случае с компенсацией сократится в раз (а не в К раз, как без нее), а спрос на второй товар в раз вырастет. В случае роста цены второго товара ситуация будет полностью симметричной. Таким образом, при , или ,.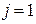

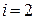
Индекс сотр означает, что перекрестная частная производная спроса рассчитывается при необходимой для поддержания прежнего уровня благосостояния компенсации дохода. Условие компенсации снимает "эффект дохода", оставляя лишь"эффект замены", что позволяет более точно определить понятие взаимозаменяемости и взаимодополняемости благ и оценивать эти характеристики.

Блага i и j называются взаимозаменяемыми, есл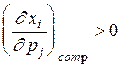и

и 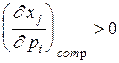(эти два условия равносильны),

и взаимодополняемыми, есл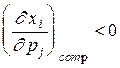и и .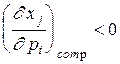

Рассчитаем теперь эти частные производные для рассматриваемой задачи, когда 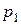растет в К раз. В этом случае приращение

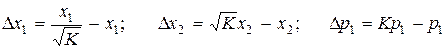. Отсюда

;

.

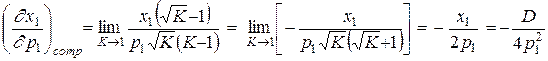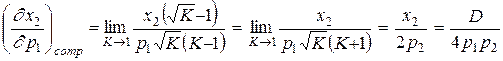Последняя величина положительна, что свидетельствует о взаимозаменяемости благ в рассматриваемой задаче.