Модель Р.Стоуна
Получим функцию спроса на примере конкретной функции потребительского предпочтения, называемой функцией Р.Стоуна и имеющей вид:
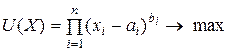 .
.
Здесь ai - минимально необходимое количество i-го блага, которое приобретается в любом случае и не является предметом выбора.
Для того чтобы набор (ai) мог быть полностью приобретен, необходимо, чтобы доход был больше количества денег, требуемого для покупки этого набора: 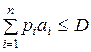 . Коэффициенты степени bi > 0 характеризуют «ценность» благ для потребителя.
. Коэффициенты степени bi > 0 характеризуют «ценность» благ для потребителя.
Модель Р.Стоуна имеет вид:
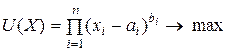 ;
;
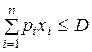 ;
; 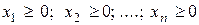 .
.
Решение находим методом Лагранжа. Приравняв нулю частные производные функции Лагранжа по переменным хi, получаем для всех i:
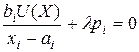 . Отсюда получаем:
. Отсюда получаем: 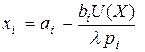 .
.
К этим условиям добавляется равенство 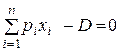 , выполнение которого эквивалентно равенству нулю частной производные функции Лагранжа по переменной l. Умножив каждое i-ое условие на l
, выполнение которого эквивалентно равенству нулю частной производные функции Лагранжа по переменной l. Умножив каждое i-ое условие на l 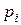 и просуммировав их по i, получим:
и просуммировав их по i, получим: 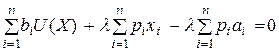 .
.
Поскольку в точке оптимума бюджетное ограничение выполняется как равенство, заменим 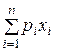 на D. Получим
на D. Получим
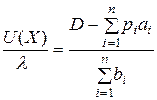
Отсюда имеем функцию спроса 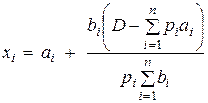 .
.
Дата добавления: 2015-04-21; просмотров: 1310;
