Примеры расчета различных цепей символическим методом
Пример 3.9. На рисунке 3.46, приведена электрическая цепь с одним источником питания, параметры которой соответственно равны: U = 100 (B), r1 = 9 (Ом), xL1 = 12 (Ом), r2 = 6 (Ом), xC2 = 8 (Ом), r3 = 10 (Ом). Требуется определить токи во всех ветвях электрической цепи символическим методом.
 |
1. Подготавливаем схему для расчета комплексов токов.
1.1. Направляем напряжение источника питания по действительной оси, т.к. комплекс вектора напряжения на входе соответственно равен:
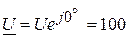(В).
1.2. Формируем комплексные сопротивления ветвей:
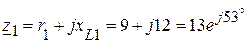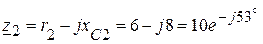(Ом),
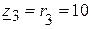(Ом),
(Ом).
1.3. Схема для определения комплексов тока имеет вид, представленный на рисунке 3.47.
2. Определяем комплексное входное сопротивление цепи.
2.1. Параллельно соединенную вторую и третью ветви, заменяем эквивалентной и определяем сопротивление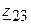 
:
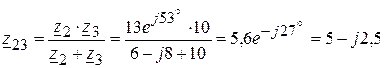(Ом).
2.2. Комплексное входное сопротивление цепи
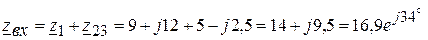(Ом).
3. Определяем комплексы токов.
3.1. Комплекс ток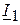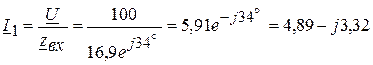а 
:
(А).
3.2. Определяем комплексы токов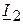 
и 
.
3.2.1. Комплексное напряжение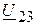 
на зажимах второй и третьей ветви:
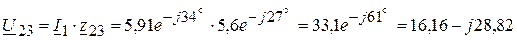(В).
3.2.2. Комплекс ток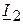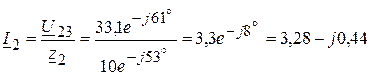а :
(А).
3.2.3. Комплекс ток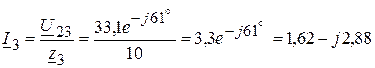а :
(А).
4. Проверяем рассчитанные комплексы токов, применяя первый закон Кирхгофа, согласно которому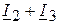 
.
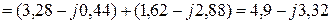Полученный результат совпадает с рассчитанным значением комплекса тока 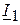. Следовательно 
.
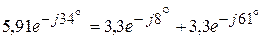Пример 3.10. На рисунке 3.48, представлена разветвленная электрическая цепь переменного тока, с параметрами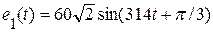 
(B), r1 = 6 (Ом), xL1 = 8 (Ом), r2 = 3 (Ом), xC2 = 4 (Ом), 
(A). Требуется определить токи во всех ветвях электрической цепи символическим методом.
1. Подготавливаем схему для расчета комплексов токов.
1.1. Формируем комплекс ЭДС и токов источников питания:
(В),
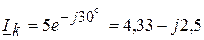(А).
1.2. Формируем комплексные сопротивления ветвей:
,
.
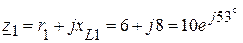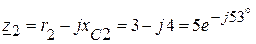1.3. Схема для определения комплексов тока имеет вид, представленный на рисунке 3.49.
2. Определим комплексы токов в ветвях методом контурных токов. Приведенная на рисунке 3.49 схема, имеет два контура. Второй контур включает в себя источник тока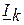 
, поэтому контурный ток второго контура определен и равен току источника тока 
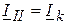. Для определения комплексных токов ветвях, достаточно определить ток первого контура 
.
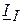2.1. Составляем уравнения для определения контурного тока.
.
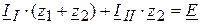2.2. Подставляем числовые значения и рассчитываем контурный ток .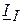
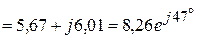(А).
2.3. Определяем комплексные токи в ветвях.
2.3.1. Ток в первой ветви 
(А).
2.3.2. Ток во второй ветви
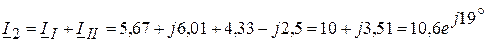(А).
Пример 3.11. Рассмотрим расчет разветвленной цепи синусоидального тока с использованием различных методов (метод непосредственного применения законов Кирхгофа, метод контурных токов, метод узловых потенциалов и др.).
На рисунке 3.50 приведена электрическая схема, с параметрами: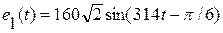 
(B), r1 = 12 (Ом), xL1 = 20 (Ом), xC1 = 11 (Ом), 
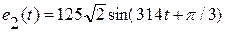(B), r2 = 8 (Ом), xC2 = 6 (Ом), r3 = 4 (Ом), 
(B), r4 = 6 (Ом), xL4 = 8 (Ом), xC5 = 5 (Ом), xL6 = 6 (Ом). Требуется определить комплексные токи во всех ветвях электрической цепи различными методами.
1. Подготовим схему для расчета комплексов тока:
1.1. Формируем комплексы ЭДС источников питания:
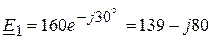(В),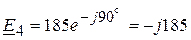 
(В), 
(В).
1.2. Формируем комплексные сопротивления ветвей:
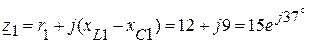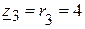(Ом);
(Ом);
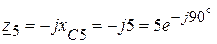(Ом);
(Ом);
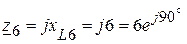(Ом);
(Ом).
1.3. Вычертим схему для определения комплексов тока (рис. 3.51):
2. Осуществляем предварительный анализ схемы.
2.1. Количество ветвей – в = 6, количество узлов – y = 4. Выбираем положительное направление токов в ветвях (рис. 3.51).
2.2. Вычерчиваем граф схемы, в котором выделяем ветви дерева и ветви связи. Для данной схемы граф имеет вид, представленный на рисунке 3.52.
Ветвями дерева приняты ветви 6,5,3. Ветви связи (1,2,4) обозначены на схеме пунктирными линиями.
2.3. Используя граф схемы, формируем независимые (главные) контуры. При формировании первого независимого контура используем 1-ю ветвь связи, дополненную 5 и 6 ветвями дерева. Соответственно, второй главный контур состоит из ветви связи 2, дополненной 3 и 5 ветвями дерева; третий главный контур состоит из ветви связи 4, дополненной 3 и 6 ветвями дерева. Положительное направление обхода контура принимаем совпадающим с направлением тока в ветви связи.
3. Решаем задачу методом непосредственного применения законов Кирхгофа (рис. 3.52).
3.1. Составляем систему уравнений по законам Кирхгофа.
3.2. По 1-му закону Кирхгофа:
(1 узел);
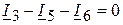(2 узел);
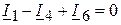(3 узел).
3.3. По 2-му закону Кирхгофа:
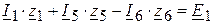(I контур);
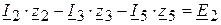(II контур);
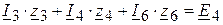(III контур).
3.4. Подставляем числовые значения в полученную систему уравнений:
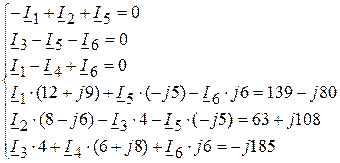
3.5. Решая данную систему уравнений, определяем токи в ветвях:
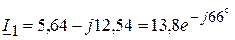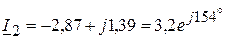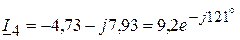(А);
(А);
(А);
(А);
(А);
(А).
4. Решаем задачу методом контурных токов (рис. 3.53).
4.1. Составляем уравнения для определения контурных токов:
;
;
.
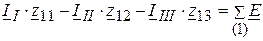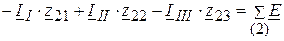4.2. Подставляем числовые значения и решаем систему уравнений:
4.2.1. Контурные сопротивления в символической форме
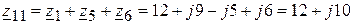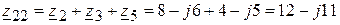(Ом);
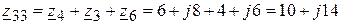(Ом);
(Ом).
Сумма сопротивлений, принадлежащих нескольким контурам
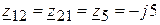(Ом);
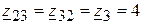(Ом);
(Ом).
Контурные ЭДС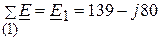 
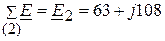(В);
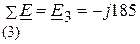(В);
(В).
4.2.2. После подстановки цифровых данных система имеет вид
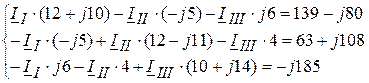
4.2.3. Решая данную систему уравнений, определяем контурные токи:
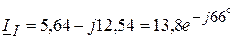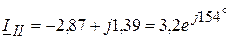(А);
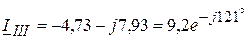(А);
(А).
4.2.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 3.53.
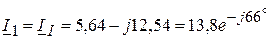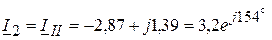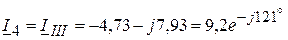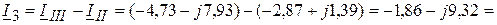
(А);
(А);
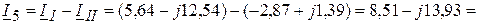
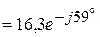(А);
(А);
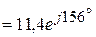(А);
(А).
5. Решаем задачу методом узловых потенциалов (рис. 3.54).
Потенциал четвертого узла принимаем равным нулю: 
. Следовательно, необходимо определить потенциалы 
, 
, 
.
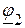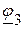5.1. Составляем уравнения для определения потенциалов , , :
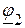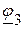5.2. Подставляем числовые значения и решаем систему уравнений.
5.2.1. Полные проводимости ветвей в комплексной форме
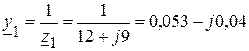(См);
(См);
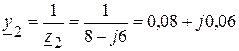(См);
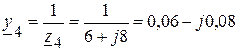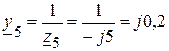(См);
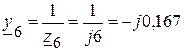(См);
(См).
5.2.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
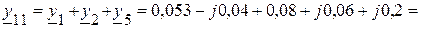
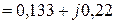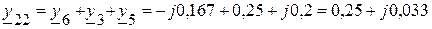(См);
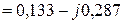(См);
(См).
Сумма проводимостей, соединяющих различные узлы
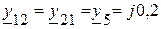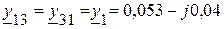(См);
(См);
(См).
Узловые токи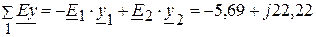 
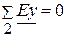(А),
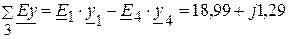(А),
(А).
5.3.2. После подстановки цифровых данных система имеет вид
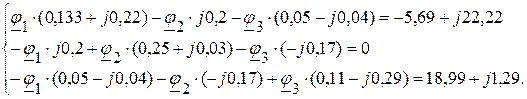
5.4. Решая данную систему уравнений произвольным методом, определяем комплексные потенциалы:
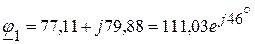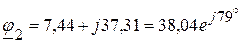(В),
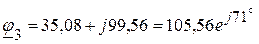(В),
(В).
5.5. Определяем токи в ветвях электрической цепи, приведенной на рис. 3.54.
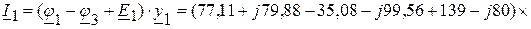
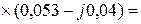
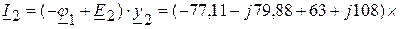
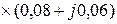
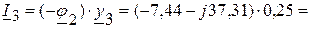
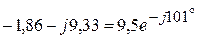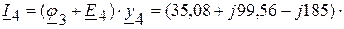
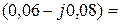
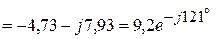(А),
(А),
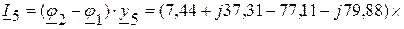
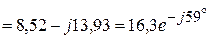(А),
(А),
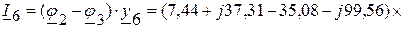
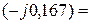
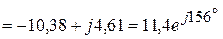(А),
(А).
6. Находим ток методом эквивалентного генератора.
6.1. Определяем напряжение холостого хода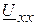 
.
6.1.1. Удаляем из исходной схемы сопротивление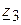 
и вычерчиваем схему активного двухполюсника (рис. 3.55).
6.1.2. Определяем токи в схеме активного двухполюсника (рис. 3.56) методом двух узлов.
Потенциал третьего узла принимаем равным нулю: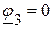 
. Следовательно, необходимо определить потенциал .
6.1.2.1. Составляем уравнение для определения потенциала :
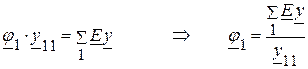
6.1.2.2. Сумма проводимостей ветвей, подключенных к первому узлу:
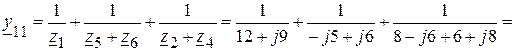
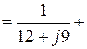
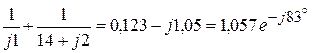(См);
Узловой ток
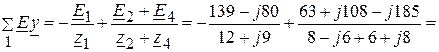
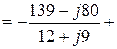
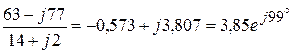(А).
6.1.2.3. После подстановки цифровых значений, определяем потенциал :
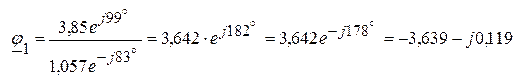(В).
6.1.2.4. Определяем токи в ветвях электрической цепи, приведенной на рисунке 3.56.
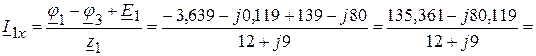
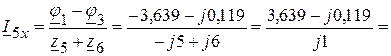
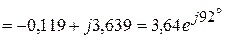(А),
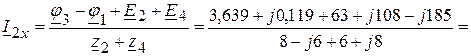
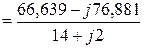
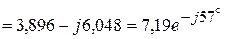(А),
(А).
6.1.3. Определяем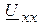 
по второму закону Кирхгофа из контура 1241
.
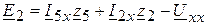Подставляем известные значения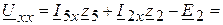 
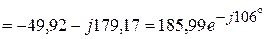(B).
6.2. Определяем входное сопротивление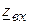 
пассивного двухполюсника.
6.2.1. Удаляем источники питания и вычерчиваем схему пассивного двухполюсника (рис. 3.57).
6.2.2. Треугольник сопротивлений 
, 
, 
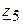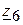преобразовываем в звезду сопротивлений (рис. 3.58,а):
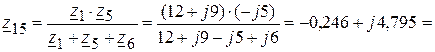
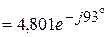(Ом),
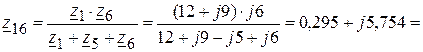
(Ом),
(Ом).
6.2.3. Последовательно соединенные элементы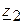 
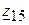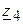и 
, 
и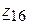 
заменяем эквивалентным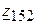и 
и 
соответственно (рис. 3.58,б):
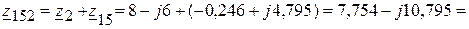
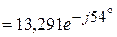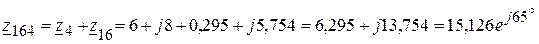(Ом),
(Ом).
6.2.4. Параллельно соединенные элементы 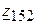и заменяем эквивалентным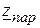 
(рис. 3.58,б):
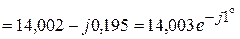(Ом).
6.2.5. Определяем входное сопротивление 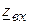(рис. 3.58,в):
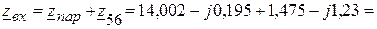
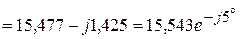(Ом).
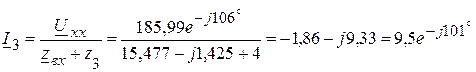6.3. Определяем ток (А).
(А).
Дата добавления: 2015-04-21; просмотров: 1364;