Модель Арбитража

В 1976 г. С.Росс предложил модель оценки доходности активов, которая получила название "Арбитражная теория оценки стоимости" (Arbitrage pricing theory - APT). В рамках модели все инвесторы имеют одинаковые ожидания относительно ожидаемой доходности активов и вероятностных распределений значений факторов риска, отсутствуют ограничения на короткие продажи. Как отмечают Р.Ролл и С.Росс, в качестве первого принципа модели выступает линейный процесс формирования доходности активов. В отличие от САРМ, в APT не делается акцент на какой-либо особый портфель, не учитывается положение об эффективности рыночного портфеля, не делаются особые предположения о функции полезности инвестора, а лишь предполагается ее монотонность и выпуклость. Модель не ограничивается одним временным периодом.

Свои рассуждения С.Росс начинает с предположения о том, что инвесторы считают: доходности активов определяются линейной моделью с факторами риска:

Коэффициент чувствительности определяется как и в модели САРМ по формуле:

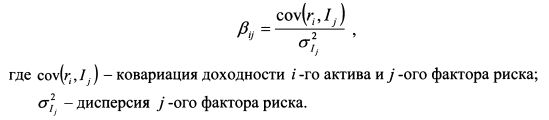
В модели предполагается, что количество активов на рынке намного больше количества факторов, влияющих на доходность активов.

Модель получила название арбитражной, так как она накладывает арбитражные ограничения на доходности активов. Это означает, что в случае нарушения равновесия на рынке, т.е. возникновения нелинейных соотношений между риском и доходностью активов, можно заработать арбитражную прибыль. В свою очередь действия арбитражеров восстановят равновесие. Арбитражная прибыль получается в результате формирования арбитражного портфеля.

С.Росс рассматривает инвестора, который владеет некоторым портфелем и анализирует варианты создания различных арбитражных портфелей на его основе. Арбитражный портфель характеризуется тем, что его формирование не связано с дополнительными издержками, так как покупка одних активов финансируется за счет средств от продажи других активов в портфеле. Таким образом, в арбитражном портфеле сумма всех удельных весов активов равна нулю:

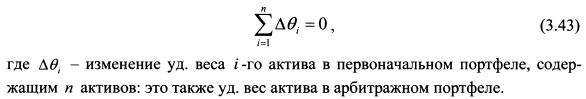
На основе уравнения (3.42) дополнительный доход, который инвестор получит от арбитражного портфеля, равен:

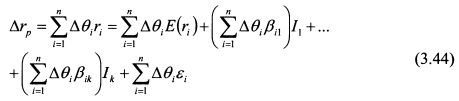
В уравнении (3.44) последнее слагаемое представляет собой специфический риск. Для широко диверсифицированного портфеля его значение практически равно нулю, поэтому им можно пренебречь.

По определению арбитражный портфель не должен быть восприимчив ни к одному фактору риска. Следовательно, удельные веса активов в портфеле можно подобрать для каждого фактора таким образом, чтобы исключить и рыночный риск. Поэтому портфель характеризуется условием:

В результате, доходность, которую получит инвестор от формирования арбитражного портфеля при нарушении равновесия на рынке, определяется только первым слагаемым в уравнении (3.44) и составляет:

В условиях равновесия доходность арбитражного портфеля должна быть равна нулю, т.е.:

Условия (3.47), (3.45) и (3.43) определяют следующий вид зависимости ожидаемой доходности актива от факторов риска:

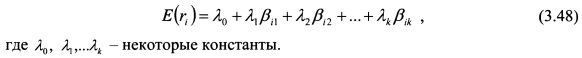
Чтобы увидеть данную зависимость, умножим уравнение (3.48) для каждого актива на значение его удельного веса в арбитражном портфеле и просуммируем полученные значения для всех активов. Для наглядности проделаем это для портфеля из трех активов при существовании двух факторов риска и, соответственно, двух коэффициентов чувствительности к факторам риска. Для каждого актива получаем результат:

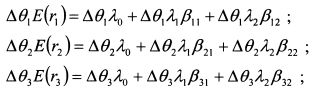
Суммируем:

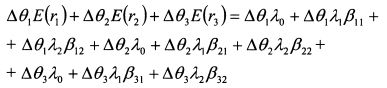
или

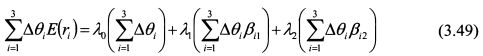
Если выполнены условия (3.43) и (3.45), то слагаемые в правой части (3.49) равны нулю, и, следовательно, выполняются зависимости (3.47) и (3.48). Зависимость (3.48) является центральным выводом модели APT.

Зависимость (3.48) можно получить и на основе стандартных рассуждений, не допускающих арбитражных ситуаций на рынке. Между риском и доходностью активов должна выдерживаться определенная закономерность. Поскольку нерыночный риск устраняется за счет диверсификации, то зависимость будет отражать только рыночный риск. Если зависимость между риском и доходностью активов не линейна, открывается возможность получить арбитражную прибыль. Проведем рассуждения для случая, когда доходности активов зависят только от одного фактора риска. Допустим, между доходностями активов и их рыночным риском, представленным коэффициентом бета, не выдерживается линейная зависимость. Пусть фактическая ситуация представлена на рисунке 4.2, т.е. бумаги располагаются на некоторой кривой. Ожидаемые доходности портфелей и их риски, измеренные коэффициентом бета, являются средневзвешенными величинами. Поэтому инвестор может образовать два портфеля. Он осуществит короткую продажу бумаги С и купит бумагу В таким образом, чтобы доходность первого портфеля составила величину E(r1). Он также осуществит короткую продажу бумаги D и купит бумагу А таким образом, чтобы доходность второго портфеля составила величину E(r2). После этого инвестор продаст менее доходный второй портфель и купит более доходный первый портфель. Арбитражная прибыль составит разницу между E(r1) и E(r2). Для корректности рассуждений необходимо учесть еще один момент. Если каждый портфель построен только из двух бумаг, то он характеризуется высоким нерыночным риском. Поэтому в рассмотренной ситуации следует формировать широко диверсифицированные портфели. Это можно сделать следующим образом.

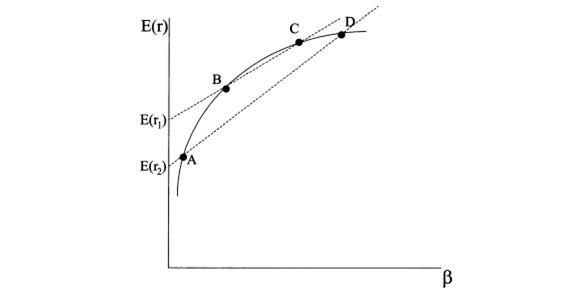
Рисунок 4.2 – Формирование арбитражного портфеля