Модель У.Шарпа

Ожидаемую доходность актива можно определить на основе индексных моделей. Их суть состоит в том, что изменение доходности и цены актива зависят от ряда показателей, характеризующих состояние рынка, или индексов.

Простая индексная модель была предложена У.Шарпом в середине 60-х годов. Цель ее разработки состояла в том, чтобы упростить процесс определения эффективной границы Марковца, сократив количество необходимых вычислений. У.Шарп назвал модель диагональной. В модели представлена зависимость между доходностью актива и значением рыночного индекса. Она предполагается линейной. Уравнение модели можно записать как:

Случайную компоненту доходности at можно разделить на две части:

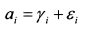
y_i является константой и представляет собой ожидаемую доходность актива при отсутствии воздействия на него рыночных факторов. ६_i - это случайная величина со средним значением равным нулю. С учетом сказанного модель принимает вид:

В формулу вводится независимая случайная переменная (ошибка): она показывает специфический риск актива, который нельзя объяснить действием рыночных сил. Значение ее средней равно нулю, дисперсия постоянна, ковариация со значением рыночного индекса равна нулю; ковариация с нерыночным компонентом доходности других активов равна нулю, т.е. 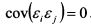. В силу центральной предельной теоремы ६ распределена нормально, поскольку на нее оказывает влияние большое количество разных факторов.

По условиям модели ожидаемое значение величины ६ равно нулю. Поэтому ожидаемое значение доходности актива E(r_i) определяется как:

Модель получила название диагональной, поскольку риск портфеля можно представить с помощью ковариационной матрицы, в которой все значения равны нулю, кроме значений, расположенных на главной диагонали. Поясним сказанное.

Доходность портфеля равна:

Подставим в формулу (3.17) формулу (3.16):

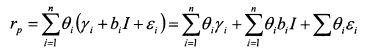
ИЛИ

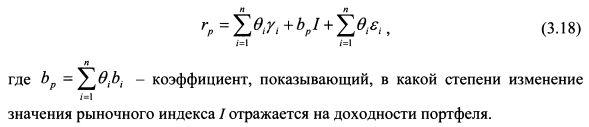
На основе формулы (3.18) дисперсия доходности портфеля равна:

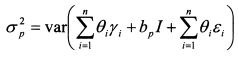
или

Формулу (3.19) можно записать в матричной форме как:

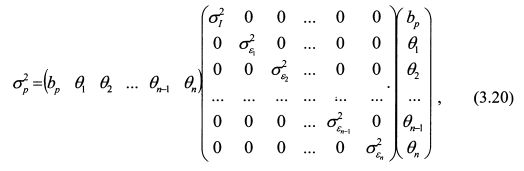
Из выражения (3.20) видно, что в ковариационной матрице по главной диагонали стоят дисперсия рыночного индекса и дисперсии специфических рисков активов портфеля. Остальные значения матрицы равны нулю.

В формуле (3.16) Дж. Трейнор заменил значение индекса показателем его доходности, чтобы оперировать однопорядковыми величинами зависимой и независимой переменных. Данную модель называют рыночной моделью. Ее уравнение имеет вид:

Если уравнение (3.21) применить для определения ожидаемой доходности портфеля, оно примет вид:

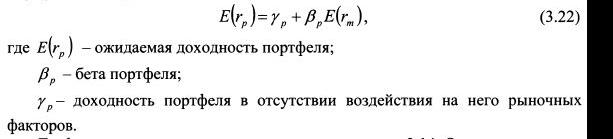
Графически рыночная модель представлена на рисунке 4.1. Она показывает зависимость между доходностью рыночного индекса (r_m) и доходностью актива (r_i и представляет собой прямую линию). Дж. Трейнор назвал ее линией характеристики. Независимой переменной выступает доходность рыночного индекса. Линия характеристики есть не что иное, как линия регрессии доходности актива на доходность рыночного индекса. Поэтому на основе метода наименьших квадратов параметры рассчитываются как:

Пример.

Средняя доходность актива А равна 20%, средняя доходность рыночного индекса - 17%, ковариация доходности актива и индекса составляет 0,04, дисперсия индекса 0,09. Определить уравнение рыночной модели.

Решение.

Бета актива А равна:

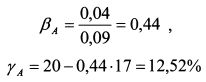
Уравнение рыночной модели имеет вид:

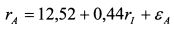
На рисунке 4.1 точками показаны конкретные значения доходности актива А и рынка для различных моментов времени в прошлом.

На рисунке 4.1 представлен случай, когда бета положительна, и поэтому график рыночной модели направлен вправо вверх, т. е. при увеличении доходности рыночного индекса доходность актива будет повышаться, при понижении - падать. При отрицательном значении беты график направлен вправо вниз, что говорит о противоположном движении доходности индекса и актива. Более крутой наклон графика говорит о высоком значении беты и большем риске актива, менее крутой наклон - о меньшем значении беты и меньшем риске.

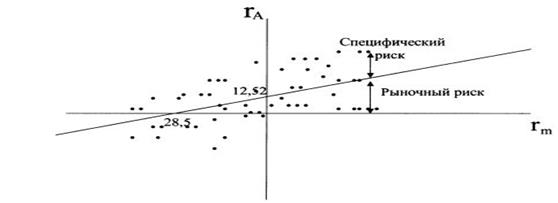
Рисунок 4.1 – Линия характеристики