Поверхность уровня

Поверхность, точки которой имеют одинаковые значения данной функции, называется поверхностью уровня (рисунок 2.3). К поверхности равного уровня относятся:

ü поверхности равного давления;

ü изотермические поверхности (поверхности равной температуры);

ü поверхности равной плотности и т.д.

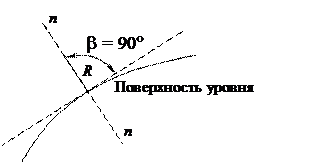
Рисунок 2.3 – Поверхность уровня

В гидравлике рассматриваются поверхности равного давления.

Принимая p = const (dp = 0) c учетом того, что для жидкости r ¹ 0 (см. рисунок 2.2), получим

.

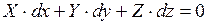Это уравнение является дифференциальным уравнением поверхности уровня (здесь X,Y,Z являются функциями координат).

Поверхности уровня обладают следующими свойствами:

Первое свойство поверхности уровня заключается в том, что две различные поверхности уровня не пересекаются между собой.

Докажем это от обратного.

Допустим, что поверхности уровня пересекаются. Тогда во всех точках линии пересечения этих поверхностей давление одновременно должно быть равно р₁ и р₂, что противоречит основной теореме гидростатики, в которой доказывается, что гидростатическое давление р одинаково по всем направлениям.Следовательно, две различные поверхности уровня не пересекаются.

Второе свойство – внешние массовые (объемные силы) направ­лены по нормали к поверхности уровня (см. рисунок 2.3).

Известно, что уравнение работы dA силы R на пути ds имеет вид

,

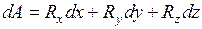где R_x, R_y и R_z – проекции силы по координатным осям Ox, Oy и Oz.

Но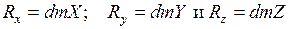

где dm – элементарная масса;

X, Y, Z – проекции ускорения силы R по тем же координатным осям.

Тогда

.

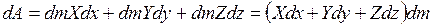Но для поверхности уровня

.

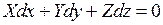Поэтому работа силы R(внешней объемной силы ) равна нулю. Следовательно, для поверхности уровня

,

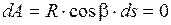где b = Ð(R,S).

Это возможно лишь при cosb = 0, т.е. внешняя сила должна быть нормальна к поверхности уровня (b = 90°).