Решение уравнения Шредингера и дискретность энергетических уровней электрона в атоме.
Состояние электрона в атоме водорода описывается волновой функцией y, удовлетворяющей стационарному уравнение Шредингера.
Решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Возможные значения Е1, Е2, Е3…, показаны на рис.23.2 в виде горизонтальных прямых. Самый нижний уровень Е1, отвечающий минимальной возможной энергии, —основной, все остальные (Еn > Е1, n = 2, 3, ...) —возбужденные. Из рисунка следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при n = ¥ E¥ = 0. При Е > 0 движение электрона являетсясвободным; область непрерывного спектра Е > 0 (заштрихована на рис. 23.2) соответствуетионизованному атому.
Собственные значения оператора квадрата момента импульса равнs
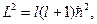 (l=0,1,2,….) (l=0,1,2,….)
| (23.5.1) |
где l-квантовое число, называемое азимутальным.
Модуль момента импульса может иметь лишь дискретные значения, определяемые формулой
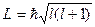 , (l=0,1,2,….) , (l=0,1,2,….)
| (23.5.2) |
Оператор проекции момента импульса на ось OZ
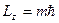 , (m=0,±1,±2,….) , (m=0,±1,±2,….)
| (23.5.3) |
где m – магнитное квантовое число. Таким образом,магнитное квантовое число m определяет проекцию момента импульса электрона на заданное направление.
Момент импульса системы, состоящей из нескольких микрочастиц, равен сумме моментов отдельных частиц. Суммарный момент, как и всякий момент, определяется
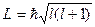 , ,
| (23.5.4) |
где l – азимутальное квантовое число результирующего момента.
Расщепление спектральных линий называется тонкой структурой. Для объяснения тонкой структуры спектральных линий, американские физики Д. Уленбек и С. Гаудсмит предположили, что у электрона помимо момента импульса L и соответствующей ему проекции момента импульса на ось OZ Lz имеется собственный механический момент импульса Ls , называемый спином электрона. Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.
Если электрону приписывается собственный механический момент импульса (спин) Ls то ему соответствует собственный магнитный момент Lsz. Согласно общим выводам квантовой механики, спин квантуется по закону:
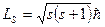
| (23.5.5) |
где s-спиновое квантовое число.
По аналогии с орбитальным моментом импульса, проекция Lsz спина квантуется так, что векторLs может принимать 2s+1 ориентации. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением:
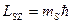
| (23.5.6) |
где ms —магнитное спиновое квантовое число; оно может иметь только два значения: тs=±1/2.
Таким образом, экспериментальные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состояния электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.
Решение задачи об энергетических уровнях электрона для атома водородоподобных систем сводится к задаче о движении электрона в кулоновском поле ядра.
Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze
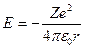 (23.5.7)
(23.5.7)
где r – расстояние между электроном и ядром.
Состояние электрона в атоме водорода описывается волновой функцией, удовлетворяющей стационарному уравнению Шредингера:
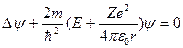 (23.5.8)
(23.5.8)
где m – масса электрона, Е - полная энергия электрона в атоме, е – заряд электрона.
Данное уравнение имеет решение, удовлетворяющее стандартным условиям, в следующих случаях: 1) при любых положительных значениях E; 2) при дискретных отрицательных значениях энергии, равных
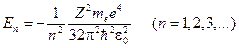 . (23.5.9)
. (23.5.9)
Случай 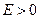 соответствует электрону, пролетающему вблизи ядра, т.е. свободному электрону. Случай
соответствует электрону, пролетающему вблизи ядра, т.е. свободному электрону. Случай 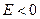 соответствует электрону, движущемуся вблизи ядра, т.е. связанному электрону. Самый нижний уровень
соответствует электрону, движущемуся вблизи ядра, т.е. связанному электрону. Самый нижний уровень 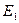 , отвечающий минимально возможной энергии, называется основным, все остальные – возбужденными. Таким образом, квантование энергии атома является следствием теории, в отличие от теории Бора, в которой квантование вводилось как постулат.
, отвечающий минимально возможной энергии, называется основным, все остальные – возбужденными. Таким образом, квантование энергии атома является следствием теории, в отличие от теории Бора, в которой квантование вводилось как постулат.
Собственные функции уравнения (23.5.8), представленные в сферической системе координат, содержат три целочисленных параметра: главное число n, орбитальное число l и магнитное число m
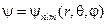 .
.
Главное число n определяет энергетический уровень электрона в атоме в соответствии с формулой (23.5.9) и может принимать любые положительные целочисленные значения.
Орбитальное число l определяет орбитальный момент импульса электрона. Согласно законам квантовой механики момент импульса квантуется по правилу
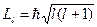 . (23.5.10)
. (23.5.10)
При заданном n орбитальное число может принимать значения
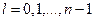 . (23.5.11)
. (23.5.11)
Магнитное число m определяет ориентацию орбитального момента в пространстве. Согласно законам квантовой механики величина проекции момента на некоторое направление z принимает дискретные значения
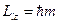
где m – магнитное квантовое число, которое при заданном l может принимать значения
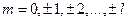 .
.
Таким образом, вектор момента импульса электрона в атоме может иметь в пространстве 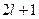 возможных ориентаций.
возможных ориентаций.
Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве.
Согласно (23.5.9) энергия электрона зависит только от главного квантового числа n. Каждому собственному значению энергии 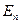 (кроме
(кроме 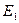 ) соответствует несколько собственных функций
) соответствует несколько собственных функций 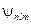 , отличающихся значениями квантовых чисел l и m. Это означает, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях.
, отличающихся значениями квантовых чисел l и m. Это означает, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях.
Состояния с одинаковой энергией называются вырожденными, а число различных состояний с каким-либо значением энергии называется кратностью вырождения соответствующего энергетического уровня.
Кратность вырождения энергетических уровней легко вычисляется путем подсчета возможных значений l и m. Каждому значению квантового числа l соответствует 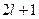 значений квантового числа m. Следовательно, число различных состояний, соответствующих данному n, равно
значений квантового числа m. Следовательно, число различных состояний, соответствующих данному n, равно
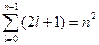 . (23.5.12)
. (23.5.12)
В атомной физике применяется условное обозначение состояний электрона с различными значениями момента импульса. Электрон, находящийся в состоянии с 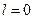 называется s-электроном (соответствующее состояние – s-состоянием), с
называется s-электроном (соответствующее состояние – s-состоянием), с  – p-электроном, с
– p-электроном, с 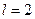 – d-электроном, с
– d-электроном, с 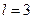 – f-электроном и далее по алфавиту. Значение главного квантового числа указывается перед условным обозначением орбитального числа l. Поскольку l всегда меньше n, возможны следующие состояния электрона:
– f-электроном и далее по алфавиту. Значение главного квантового числа указывается перед условным обозначением орбитального числа l. Поскольку l всегда меньше n, возможны следующие состояния электрона:
1s,
2s, 2p,
3s, 3p, 3d
и т.д.
Испускание и поглощение света происходит при переходах электрона с одного уровня на другой. В квантовой механике доказывается, что для орбитального квантового числа имеется правило отбора
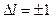 . (23.5.13)
. (23.5.13)
Это означает, что возможны только такие переходы, при которых l меняется на единицу. Правило обусловлено тем, что фотон обладает собственным моментом импульса (спином s). Его величина вычисляется по общему правилу (23.5.10), где вместо l следует использовать 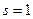 . Данное значение определяет максимальную величину проекции спина на избранное направление. Испускание или поглощение фотона, согласно закону сохранения момента импульса, приводит к изменению момента импульса атома, согласно с правилом (23.5.13).
. Данное значение определяет максимальную величину проекции спина на избранное направление. Испускание или поглощение фотона, согласно закону сохранения момента импульса, приводит к изменению момента импульса атома, согласно с правилом (23.5.13).
Учитывая число возможных состояний, соответствующих данному n, и правило отбора, рассмотрим спектральные линии атома водорода:
серии Лаймана соответствуют переходы:
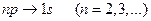 ;
;
серии Бальмера соответствуют переходы:
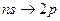 и
и 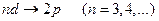 ,
,
и т.д.
Переход электрона из основного состояния в возбужденное обусловлен увеличением энергии атома и может происходить только при сообщении атому энергии извне., например, за счет поглощения атомом фотона.
Дата добавления: 2015-04-19; просмотров: 1418;
