Квантовая статистика. Фазовое пространство. Функция распределения

Квантовая статистика – раздел статистической физики, исследующий системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.

Рассмотрим систему из N частиц. Свяжем с ней многомерное пространство всех координат и импульсов частиц системы. Состояние системы определяется заданием переменных 6N, так как состояние каждой частицы определяется тройкой координат x, y, z и тройкой проекций импульса р_x, p_y, p_z. Поэтому размерность многомерного пространства равно 6N. Это пространство называется фазовым пространством. Каждому микросостоянию системы в классическом случае отвечает точка в фазовом пространстве. При квазиклассическом описании движения системы на каждое квантовое состояние системы приходится в этом пространстве элементарный объем .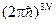

При взаимодействии с окружающей средой состояние системы меняется. Вероятность dР некоторого состояния системы (p, q) можно представить с помощью функции распределения f (p,q):

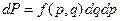(24.1.1)

По определению функции распределения

,

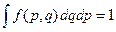где интегрирование производится по всему фазовому пространству.

При известной функции распределения f (p,q) можно определить макроскопические параметры системы. Любой макроскопический параметр L в смысле статистической физики является средним по микросостояниям

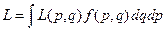. (24.1.2)

Явное выражение функции распределения для системы, находящейся в тепловом контакте с большим тепловым резервуаром было получено Гиббсом. Оно называется каноническим распределением Гиббса и имеет вид

,

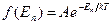где A – нормировочная постоянная, n – совокупность квантовых чисел, определяющих данное состояние.