Статистика Бозе-Эйнштейна и Ферми-Дирака.

Наиболее простым объектом для изучения является идеальный газ. Реальный газ можно считать идеальным, если взаимодействие частиц несущественно. Состояние системы невзаимодействующих тождественных частиц можно характеризовать с помощью чисел заполнения N_i, определяющих среднее число частиц в i-м квантовом состоянии.

Для систем частиц, образованных бозонами, числа заполнения могут принимать любые целые неотрицательные значения: 0, 1, 2, …. Для систем, образованных фермионами, числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых. Сумма всех чисел заполнения равна числу частиц системы. С помощью канонического (или большого канонического) распределения Гиббса можно определить числа заполнения квантовых состояний.

Числа заполнения идеального газа бозонов – бозе-газа – определяются соотношением

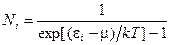. (24.2.1)

Это выражение называется распределением Бозе-Эйнштейна. Здесь N_i - среднее число бозонов в квантовом состоянии с энергией ε_i, m – параметр, который называется химическим потенциалом. Его величина определяется из условия 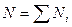, где N – число частиц в системе. Химический потенциал по своему определению является функцией числа частиц и температуры .

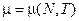Распределение фермионов по энергиям имеет вид

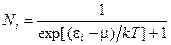. (24.2.2)

Смысл входящих в (24.2.2) величин тот же, что и в (24.2.1). Распределение (24.2.2) называется распределением Ферми-Дирака.

Если 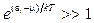, то распределения Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла-Больцмана

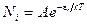, (24.2.3)

где 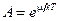. Таким образом, при малых числах заполнения ( 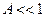) оба квантовых газа ведут себя подобно классическому газу.