Описательная статистика

Описательная статистика используется для простого обобщения данных, полученных в рамках выборочного исследования.К базовым методам описательной статистики относятся

·процентные показатели,

·меры центральной тенденции,

·меры вариации,

·парные коэффициенты связи.

I. Процентные показатели используются для того, чтобы частотное распределение по той или иной переменной привести к основе 100 (аналогично, пропорции используются для приведения данных к основе 1). В таком виде данные являются более предпочтительными в интуитивном смысле по сравнению с «сырым» частотным распределением.

Пример (успешность сдачи сессии):

Успешность Частота % Пропорции

Есть тройки 28 45,2 0,452

Нет троек, в основном четыре 11 17,7 0,177

Нет троек, в основном пять 13 21,0 0,210

На отлично 10 16,1 0,161

Всего 62 100,0 1,000

II. Меры центральной тенденции (мода, медиана и среднее арифметическое) дают информацию о типичном или центральном значении распределения.Модаговорит о наиболее часто встречающемся значении, медиана – о серединном значении, среднее арифметическое– о наиболее ожидаемом значении.

В приведенном выше примеремодойбудет вариант ответа «Есть тройки», так как его отметило 28 человек – больше, чем любой другой вариант.

Для того чтобы найти медиану, необходимо:

1) Упорядочить(по смыслу, а не по значению частоты) все варианты ответа по возрастанию или убыванию :

Есть тройки 28

Нет троек, в основном четыре 11

Нет троек, в основном пять 13

На отлично 10

2) Если количество наблюдений нечетное, необходимо найти то значение, которое будет стоять посередине этого упорядоченного ряда. Оно и будет медианой. Если же количество наблюдений четное, надо взять два значения которые стоят посередине и найти их среднее значение.

В данном случае 62 наблюдения, то посередине будет стоять 31 и 32 наблюдение. Это варианты «Без троек, в основном на четыре». Следовательно, медианойтакже будет значение «Нет троек, в основном четыре».

В данном случае расчет среднего значения не совсем корректен. Но если присвоить вариантам ответов конкретные числовые значения (например, 1, 2, 3, 4 или 3, 4, 4.5, 5), то можно осуществить расчет среднего,например:

М = (3*28 + 4*11 + 4.5*13 + 5*10)/62 = 3.815

III. Меры вариативности говорят о степени неоднородности распределения, к таким показателям относят, например:

· размах,

· коэффициент изменчивости категорий,

· стандартное отклонение и др.).

Размах (R)определяют как разницу между наибольшим и наименьшим значениями распределения. Например, если наименьше значние измеряемой в ходе эксперимента величины 147, а наибольшее – 198, то размах = 51.

Коэффициент изменчивости категорий (IQV)принимает значения в диапазоне от 0 (отсутствие изменчивости) до 1 (максимальная изменчивость), рассчитывается по формуле

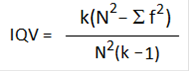
где k – количество категорий переменной, N – общее количество наблюдений в выборке, ∑f^2 – сумма квадратов частот.

Есть тройки 28 784

Нет троек, в основном четыре 11 121

Нет троек, в основном пять 13 169

На отлично 10 100

IQV = 4*(62^2 - 784-121-169-100)/ ( 62^2 (4-1)) = 0.926

Стандартное отклонение(среднеквадратичное отклонение, СКО, выборочное стандартное отклонение ) — очень распространенный показатель рассеяния в описательной статистике. Основные программы обработки данных имеют встроенную функцию вычисления стандартного отклонения. Например, в Microsoft Excel эта функция называется СТАНДОТКЛОН.

Вручную вычислить стандартное отклонение можно по формуле

STD = √ [ ( ∑(x-xi )²)/n ] , или

STD = √ [ ( ∑(x-xi )²)/( n-1) ] ,

(квадратный корень из суммы квадратов разностей между элементами выборки и средним, деленной на количество элементов в выборке ( при этом, если количество элементов в выборке превышает 30, то знаменатель дроби под корнем принимает значение n-1. Иначе используется n.)

Важно отметить, что элементы выборки в среднем отличается от среднего значения на ± STD.

IV. Парные коэффициенты связи предназначены для анализа силы и направления связей между (например, V-Крамера для номинальных шкал и Гамма для порядковых шкал).

Пример построения таблиц сопряженности

Даны таблицы исходных данных

Успешность Пол Всего

Женский Мужской

Есть тройки 16 12 28

Нет троек 20 4 24

На отлично 10 0 10

Всего 46 16 62

Таблицы сопряженности предназначены для представления данных о связи между двумя переменными. Для улучшения информативности расчитаем процентные величины в отдельности для каждого столбца. Для приведенного примера, соответствующая таблица будет выглядеть следующим образом:

Успешность Пол Всего

Женский Мужской

Есть тройки 34,8% 75,0% 45,2%

Нет троек 43,5% 25,0% 38,7%

На отлично 21,7% 0% 16,1%

Всего 100% 100% 100%

Данная таблица весьма наглядно показывает связи "оценки-студентки (девушки)", "оценки-студенты(юноши)", "оценки-студенты".