Динамика материальной точки и поступательного движения твердого тела
Первый закон Ньютона
Динамика – раздел механики, в котором изучается движение тел с учетом причин, вызывающих или изменяющих это движение. Классическая динамика базируется на трех законах Ньютона.
Первый закон Ньютона гласит: всякое тело сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.
Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции, а движение тела, свободного от внешних воздействий – движением по инерции.
Система отсчета, в которой справедлив закон инерции, называется инерциальной системой отсчета. Всякая система отсчета, движущаяся относительно инерциальной системы отсчета поступательно, равномерно и прямолинейно, является также инерциальной системой отсчета.
Инерциальная система отсчета может рассматриваться как модель, к которой реальная система отсчета имеет ту или иную степень приближения. Достаточно близка к инерциальной системе отсчета гелиоцентрическая система, начало которой совпадает с центром масс Солнечной системы, а оси координат направлены на три звезды.
Сила
Для описания механического действия тел друг на друга вводят понятие силы. Силой,действующей на тело, называют физическую величину, являющуюся мерой механического действия на это тело со стороны какого-либо другого тела, в результате которого тело приобретает ускорение или изменяет форму и размеры.
Механическое взаимодействие может осуществляться как между непосредственно контактирующими телами (например, при ударе, трении, давлении друг на друга и т. п.), так и между удаленными телами.
Особая форма материи, связывающая частицы вещества в единые системы и передающая с конечной скоростью действие одних частиц на другие, называется физическим полем или просто полем.
Взаимодействие между удаленными телами осуществляется посредством связанных с ними гравитационных и электромагнитных полей.
Пользуясь понятием силы, в механике обычно говорят о движении и деформации рассматриваемого тела под действием приложенных к нему сил. При этом конечно, каждой силе всегда соответствует какое-то определенное тело или поле, действующее с этой силой.
Сила F полностью задана, если указаны ее модуль F, направление в пространстве и точка приложения.
Прямая, вдоль которой направлена сила, называется линией действия силы. Центральными называются силы, которые всюду направлены вдоль прямых, проходящих через одну и ту же неподвижную точку - центр сил, и зависят только от расстояния до центра сил.
Поле, действующее на материальную точку с силой F, называется стационарным полем, если оно не изменяется с течением времени.
Единица силы - ньютон (Н): 1Н - сила, которая массе в 1кг сообщает ускорение 1м/с2 в направлении действия силы.
Если на тело действуют одновременно n сил 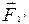
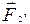 …
… 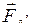 приложенных в одной и той же точке A тела, то n сил можно заменить одной силой
приложенных в одной и той же точке A тела, то n сил можно заменить одной силой 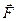 , равной их геометрической сумме
, равной их геометрической сумме
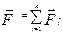
| (2.1.1) |
где 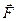 - результирующая или равнодействующая сила.
- результирующая или равнодействующая сила.
Масса. Второй закон Ньютона
Эксперимент показывает, что под действием силы 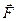 свободное тело изменяет скорость своего поступательного движения, приобретая ускорение
свободное тело изменяет скорость своего поступательного движения, приобретая ускорение 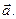 Второй закон Ньютона справедлив в инерциальной системе отсчета и устанавливает связь между ускорением тела и силами, действующими на него: ускорение, приобретаемое телом, пропорционально равнодействующей всех сил
Второй закон Ньютона справедлив в инерциальной системе отсчета и устанавливает связь между ускорением тела и силами, действующими на него: ускорение, приобретаемое телом, пропорционально равнодействующей всех сил 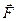 , действующих на тело, и обратно пропорционально его массе т
, действующих на тело, и обратно пропорционально его массе т
 . .
| (2.1.2) |
В ньютоновской механике, в основе которой лежат законы Ньютона, масса тела характеризует инерционные свойства тела, не зависит от положения тела в пространстве, его скорости, действия на тело других тел и т.д. Масса является величиной аддитивной, т.е. масса тела равна сумме масс всех его частей. Однако свойство аддитивности утрачивается при скоростях, близких к скорости света в вакууме, т.е. в релятивистской механике. За основную единицу массы, называемую килограммом (кг), принимают массу эталонного тела, хранящегося в международном бюро мер и весов.
Уравнение (2.1.2) описывает изменение движения протяженного тела под действием силы только при условии, что тело: 1) не деформируется, и 2) движется поступательно. В противном случае ускорения разных точек тела неодинаковы, и изменение движения всего тела (системы материальных точек) нельзя описать с помощью единого ускорения 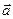 . Для материальной точки условия 1) и 2) всегда выполняются, и поэтому формулу (2.1.3) называют основным уравнением динамики материальной точки.
. Для материальной точки условия 1) и 2) всегда выполняются, и поэтому формулу (2.1.3) называют основным уравнением динамики материальной точки.
Если на материальную точку действуют несколько сил, то 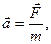 где
где 
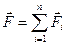 (2.1.1):
(2.1.1):
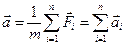 . .
| (2.1.4) |
Таким образом, если на материальную точку одновременно действуют несколько сил, то каждая из них сообщает материальной точке такое же ускорение, как если бы других сил не было – формулировка принципа независимости действия сил.
Импульс материальной точки
Импульсом или количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость:
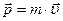
Единица измерения импульса - 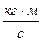 .
.
Импульс является одной из важнейших динамических характеристик, зависящей как от быстроты движения материальной точки, так и от ее инертности. Используя выражение (1.1.9) можно показать, что:
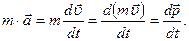
С другой стороны, согласно (2.1.2), 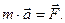 Следовательно
Следовательно
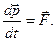
| (2.1.5) |
Уравнение (2.1.5) является одним из математических выражений второго закона Ньютона: скорость изменения импульса материальной точки равна силе, действующей на точку. Из (2.1.6) следует, что 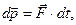 где
где 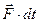 - элементарный импульс силы за малый промежуток времени dt. Таким образом, изменение импульса материальной точки за малый промежуток времени dt равно элементарному импульсу результирующей силы (за тот же промежуток времени), действующей на материальную точку.
- элементарный импульс силы за малый промежуток времени dt. Таким образом, изменение импульса материальной точки за малый промежуток времени dt равно элементарному импульсу результирующей силы (за тот же промежуток времени), действующей на материальную точку.
Соответственно изменение импульса материальной точки за время от t1 до t2: 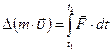 - импульс силы за это же время. Если
- импульс силы за это же время. Если 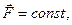 то
то 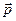 - линейная функция от времени t:
- линейная функция от времени t:
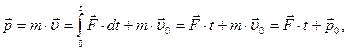
| (2.1.6) |
где υ0 – начальная скорость материальной точки (при t = 0). При 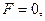
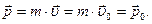 Из (2.1.6) следует, что за промежуток времени Dt = t2 - t1
Из (2.1.6) следует, что за промежуток времени Dt = t2 - t1
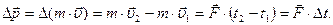
| (2.1.7) |
Если 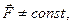 то
то
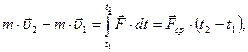
| (2.1.8) |
где  - среднее значение переменной силы за промежуток времени Dt.
- среднее значение переменной силы за промежуток времени Dt.
Третий закон Ньютона. Движение центра инерции
Механическое воздействие двух тел друг на друга всегда представляет собой их взаимодействие. На основе количественного анализа механического взаимодействия тел Ньютон установил свой третий закон динамики, который гласит: действия двух тел друг на друга всегда равны и направлены по одной прямой в противоположные стороны, то есть
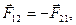
| (2.1.9) |
 |
Здесь
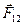 - сила, действующая на тело 1 со стороны тела 2, а
- сила, действующая на тело 1 со стороны тела 2, а 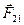 - наоборот, соответственно (рис.2.1). Третий закон Ньютона является существенным дополнением к первому и второму законам Ньютона.
- наоборот, соответственно (рис.2.1). Третий закон Ньютона является существенным дополнением к первому и второму законам Ньютона.
В механике Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс.
Центром инерции или центром масс системы материальных точек называют такую точку C, радиус - вектор которой определяется следующим выражением:
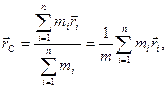
| (2.1.10,а) |
где 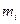 и
и 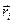 - масса и радиус-вектор i-ой материальной точки системы; m – общая масса всей системы; n – число материальных точек в системе. Соответственно декартовые компоненты центра масс
- масса и радиус-вектор i-ой материальной точки системы; m – общая масса всей системы; n – число материальных точек в системе. Соответственно декартовые компоненты центра масс 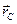 равны:
равны:
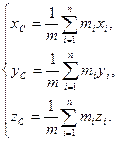
| (2.1.10,б) |
Найдем скорость движения центра инерции системы:
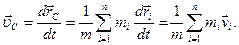
| (2.1.11) |
Геометрическую сумму импульсов всех материальных точек системы называют импульсом системы 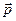 :
: 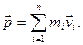 Следовательно, из (2.1.11)
Следовательно, из (2.1.11)
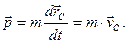
| (2.1.12) |
Тела, не входящие в состав рассматриваемой механической системы, называют внешними, а силы, действующие на систему со стороны этих тел – внешними силами. Силы взаимодействия между телами системы называют внутренними силами. Если 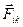 - сила, действующая на i-ую материальную точку со стороны k-ой, то результирующая со стороны всех внутренних сил, приложенных к i-ой точке, равна:
- сила, действующая на i-ую материальную точку со стороны k-ой, то результирующая со стороны всех внутренних сил, приложенных к i-ой точке, равна:
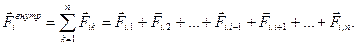
| (2.1.13) |
В уравнении (2.1.13) k пробегает значения от 1 до n, кроме i, так как i-ая точка не может действовать сама на себя.
Пусть на i-ую материальную точку действует внешняя сила 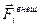 , при этом по второму закону Ньютона (2.1.6) для системы материальных точек можно записать следующие уравнения:
, при этом по второму закону Ньютона (2.1.6) для системы материальных точек можно записать следующие уравнения:
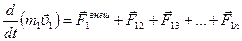
 …………………………………………..
…………………………………………..
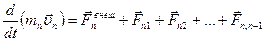
| (2.1.14) |
Складывая почленно уравнения (2.1.14), и группируя попарно силы 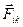 и
и 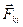 , можно получить:
, можно получить: 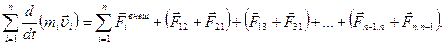 Согласно третьему закону Ньютона (2.1.9)
Согласно третьему закону Ньютона (2.1.9) 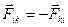 и, как следствие,
и, как следствие, 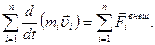
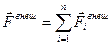 - называют главным вектором внешних сил. С другой стороны,
- называют главным вектором внешних сил. С другой стороны, 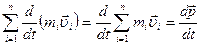 , то есть
, то есть
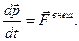
| (2.1.15,а) |
Уравнение (2.1.15,а) называют основным уравнением динамики поступательного движения системы материальных точек, которое показывает, что скорость изменения импульса механической системы равна главному вектору всех внешних сил, действующих на эту систему. В проекциях на декартовые оси выражение (2.1.15,а) примет вид:
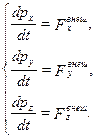
| (2.1.15,б) |
В (2.1.15,б) 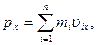
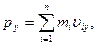
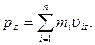 С помощью уравнения (2.1.12) можно переписать (2.1.15,а)
С помощью уравнения (2.1.12) можно переписать (2.1.15,а)
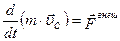 или или 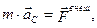
| (2.1.16) |
где  - ускорение центра инерции. Таким образом, центр инерции механической системы движется как материальная точка, масса которой равна массе всей системы, и на которую действует сила, равная главному вектору внешних сил, приложенных к системе.
- ускорение центра инерции. Таким образом, центр инерции механической системы движется как материальная точка, масса которой равна массе всей системы, и на которую действует сила, равная главному вектору внешних сил, приложенных к системе.
В общем случае движение твердого тела можно рассматривать как сумму двух движений: 1) поступательного со скоростью, равной скорости центра масс, и 2) вращательного вокруг центра инерции (С). Поэтому уравнение (2.1.16) часто называют основным уравнением динамики поступательного движения твердого тела.
Закон сохранения импульса
Механическую систему называют замкнутой или изолированной, если на нее не действуют внешние силы, то есть если она не взаимодействует с внешними телами. Для замкнутой системы главный вектор внешних сил тождественно равен нулю. Поэтому из выражения (2.1.15,а) следует закон, который называют законом сохранения импульса: импульс замкнутой системы не изменяется с течением времени, то есть
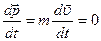 и и 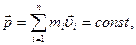
| (2.1.17) |
где 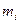 и
и 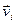 - масса и скорость i-ой материальной точки системы. Так как из (2.1.12) известно, что
- масса и скорость i-ой материальной точки системы. Так как из (2.1.12) известно, что 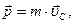 то, используя уравнение (2.1.17), можно показать, что при любых процессах, происходящих в замкнутой системе, скорость ее центра инерции сохраняется неизменной.
то, используя уравнение (2.1.17), можно показать, что при любых процессах, происходящих в замкнутой системе, скорость ее центра инерции сохраняется неизменной.
Если система не замкнута, но главный вектор внешних сил 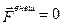 , то уравнение (2.1.17) справедливо и в открытой системе. Обычно приходится иметь дело с незамкнутыми системами, для которых
, то уравнение (2.1.17) справедливо и в открытой системе. Обычно приходится иметь дело с незамкнутыми системами, для которых 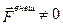 и, как следствие,
и, как следствие, 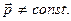 Однако если проекция главного вектора внешних сил на какую-либо ось, неподвижную относительно инерциальной системы отсчета, тождественно равна нулю, то проекция на эту же ось вектора импульса системы не зависит от времени. Например, если
Однако если проекция главного вектора внешних сил на какую-либо ось, неподвижную относительно инерциальной системы отсчета, тождественно равна нулю, то проекция на эту же ось вектора импульса системы не зависит от времени. Например, если 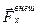 = 0, то
= 0, то 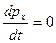 и, следовательно, рx = const – закон сохранения проекции импульса.
и, следовательно, рx = const – закон сохранения проекции импульса.
При соударении тел друг с другом они претерпевают деформации. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации или в так называемую внутреннюю энергию тел. Увеличение внутренней энергии тел сопровождается повышением температуры. Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий.
Рассмотрим применение закона сохранения импульса (2.1.17) на примере удара двух тел.
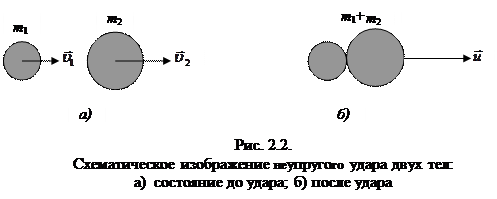 |
Ударом называется явление изменения скорости тел на конечные величины за очень малый промежуток времени, происходящее при столкновении тел. Общую нормаль к поверхностям соударяющихся тел в точке их соприкосновения называют линией удара. Удар называют прямым, если перед ударом скорости центров инерции соударяющихся тел параллельны линии удара. Удар называют центральным, если центры инерции соударяющихся тел лежат на линии удара.
Прямой центральный удар называют абсолютно неупругим, если после удара тела движутся как одно целое (рис.2.2). Если скорости двух тел до удара соответственно равны – 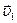 и
и 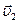 , а массы их определяются значениями m1 и m2, то общая скорость тел после абсолютно неупругого удара
, а массы их определяются значениями m1 и m2, то общая скорость тел после абсолютно неупругого удара 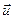 , согласно уравнению (2.1.17), может быть представлена в виде:
, согласно уравнению (2.1.17), может быть представлена в виде:
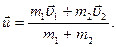
| (2.1.18) |
Дата добавления: 2015-04-19; просмотров: 2231;
