Угловая скорость
Угловой скоростью тела называют вектор 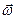 , численно равный первой производной угла j по времени, направленный вдоль оси вращения по правилу буравчика, так же как вектор
, численно равный первой производной угла j по времени, направленный вдоль оси вращения по правилу буравчика, так же как вектор 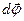 :
:
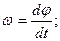 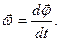
| (1.2.1.) |
Угловая скорость 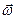 (единица измерения в СИ -
(единица измерения в СИ - 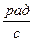 ) характеризует направление и быстроту вращения тела вокруг оси. Если
) характеризует направление и быстроту вращения тела вокруг оси. Если 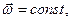 то движение называют равномерным вращением вокруг неподвижной оси.
то движение называют равномерным вращением вокруг неподвижной оси.
Скорость 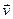 произвольной точки M тела, вращающегося с угловой скоростью
произвольной точки M тела, вращающегося с угловой скоростью 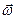 , часто называют линейной скоростью этой точки.
, часто называют линейной скоростью этой точки.
линейная скорость υ точки связана с угловой скоростью ω и радиусом R траектории соотношением
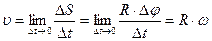 ,
,
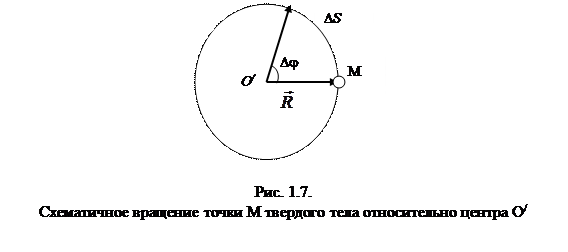 |
где DS – путь, который проходит точка за время Dt (рис.1.7.).
В векторном виде формулу для линейной скорости можно записать как векторное произведение
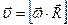 . .
| (1.2.2,а) |
Модуль линейной скорости
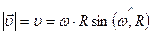 . (1.2.2,б)
. (1.2.2,б)
При равномерном вращении угловая скорость 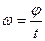 , а угол поворота
, а угол поворота 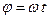 .
.
Единицей угловой скорости в системе СИ является радиан в секунду  .
.
Угловая скорость w - есть величина постоянная, она указывает, на какой угол поворачивается тело за единицу времени. В этом случае она называется круговой или циклической частотой.
Равномерное движение можно охарактеризовать также периодом обращения. Периодом вращения T называют промежуток времени, в течении которого тело равномерно вращаясь с угловой скоростью w, совершает один оборот, то есть j = 2p:
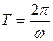
Частотой вращения n называют число оборотов, совершаемых телом за 1 секунду при равномерном вращении:
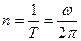 , , 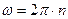
| (1.2.3) |
Единица частоты вращения – герц (Гц).
Угловое ускорение
Быстрота изменения угловой скорости характеризуется угловым ускорением 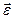 (в СИ единицей углового ускорения является
(в СИ единицей углового ускорения является 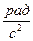 ):
):
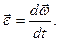
| (1.2.4,а) |
 |
При неподвижной оси вращения векторы
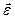 и
и 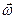 коллинеарны и направлены вдоль оси вращения. При ускоренном вращении
коллинеарны и направлены вдоль оси вращения. При ускоренном вращении 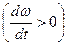 векторы
векторы 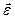 и
и 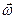 одинаково направлены, при замедленном вращении
одинаково направлены, при замедленном вращении 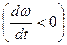 - противоположно направлены.
- противоположно направлены.
Направим ось OZ по оси вращения OO/(см. рис. 1.8), при этом проекция вектора 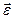 на ось OZ:
на ось OZ:
 . .
| (1.2.4,б) |
Ускорение 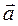 произвольной точки M тела, вращающегося с угловым ускорением
произвольной точки M тела, вращающегося с угловым ускорением 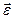 , называют линейным ускорением этой точки. Согласно выражению (1.1.12) линейное ускорение представляет собой векторную сумму тангенциального и нормального ускорений точки M твердого тела, причем,
, называют линейным ускорением этой точки. Согласно выражению (1.1.12) линейное ускорение представляет собой векторную сумму тангенциального и нормального ускорений точки M твердого тела, причем, 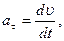 а
а 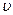 =w×R (см. (1.2.2,а)) и, как следствие,
=w×R (см. (1.2.2,а)) и, как следствие, 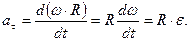 Что касается нормального ускорения
Что касается нормального ускорения 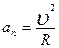 , то с учетом уравнения (1.2.2,а) можно получить:
, то с учетом уравнения (1.2.2,а) можно получить: 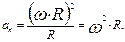 Таким образом, модуль линейного ускорения равен
Таким образом, модуль линейного ускорения равен
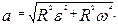
| (1.2.5) |
Из рис. 1.8 следует, что вектор тангенциального ускорения 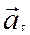 , сонаправленный с вектором линейной скорости
, сонаправленный с вектором линейной скорости 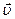 , перпендикулярен как вектору
, перпендикулярен как вектору 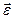 , так и вектору
, так и вектору 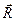 , и направлен в ту же сторону, что и результат векторного произведения
, и направлен в ту же сторону, что и результат векторного произведения 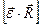 Таким образом,
Таким образом,
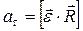
| (1.2.6,а) |
С учетом того, что  (см. рис. 1.8), можно показать:
(см. рис. 1.8), можно показать:
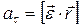
| (1.2.6,б) |
Нормальное ускорение направлено противоположно радиусу - вектору 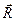 проведенному в точку M из центра окружности (по которой движется точка M) (см. рис. 1.8). Поэтому
проведенному в точку M из центра окружности (по которой движется точка M) (см. рис. 1.8). Поэтому
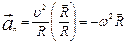
| (1.2.6,в) |
где 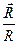 - единичный вектор, направленный по радиусу - вектору
- единичный вектор, направленный по радиусу - вектору 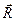
уравнения кинематики вращательного движения твердого тела относительно оси OZ OO/
1. Равномерное вращение.
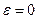 , wz = w = const > 0. При этом (см. (1.2.1))
, wz = w = const > 0. При этом (см. (1.2.1))
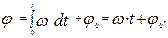
| (1.2.7) |
где j0 – значение j в начальный момент времени (t = 0).
2. Равнопеременное вращение относительно оси OZ.
ez = const. При ez > 0 – вращение равноускоренное; При ez < 0 – вращение равнозамедленное; wz = w = const > 0. Из выражения (1.2.4,б) следует, что

| (1.2.8) |
где w0 – начальная скорость. Кроме того,
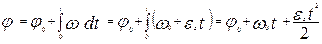 . .
| (1.2.9) |
Часто для простоты записи в выражениях (1.2.8) и (1.2.9) вместо ez используют e.
Путь, который проходит твердое тело при равноускоренном вращательном движении
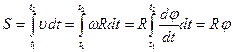 .
.
В целом полученные выше сведения по кинематике можно занести в таблицу аналогий (табл. 1).
Таблица 1
| Поступательное движение | Вращательное движение | Формулы связи |
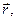 S S
| 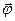
| S = R×j |
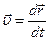
| 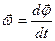
| 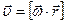
|
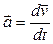
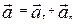
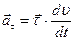

| 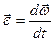
| 
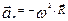
|
| Равномерное движение | ||
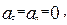 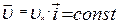
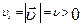
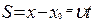
| 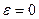 ,
wz = w = const > 0 ,
wz = w = const > 0
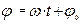
| |
| Равнопеременное движение | ||
 an = 0, at = const an = 0, at = const 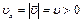
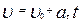
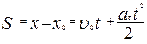
|  ez = const;
wz = w = const > 0 ez = const;
wz = w = const > 0
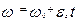
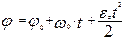
|
Дата добавления: 2015-04-19; просмотров: 1855;
