Закон Ома для однородного участка цепи. Сопротивление проводников.
Г. Ом в 1826 г. экспериментально установил закон, который называется законом Ома для однородного участка цепи:Ток, текущий по однородному металлическому проводнику, пропорционален падению напряжения на проводнике.
I= 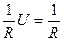 (
( 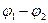 ), (12-14)
), (12-14)
где R - сопротивление проводника, измеряется в СИ в омах [Ом]; из (12-14) следует, что 1Ом =1 В/1 А.
Сопротивление проводника
R =ρl / S , (12-15)
где 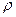 - удельное сопротивление, измеряется в СИ вОм ×м. Оно зависит от температуры:
- удельное сопротивление, измеряется в СИ вОм ×м. Оно зависит от температуры: 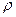 =
= 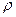
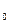
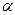 T, где
T, где 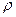
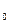 - удельное сопротивление при температуре t = 0°С,
- удельное сопротивление при температуре t = 0°С, 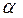 - температурный коэффициент сопротивления, близкий к 1/273 К
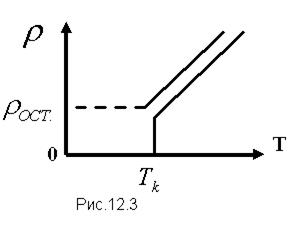
- температурный коэффициент сопротивления, близкий к 1/273 К 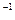 , T- термодинамическая температура; так что с ростом температуры сопротивление металлических проводников увеличивается. Качественная температурная зависимость удельного сопротивления металлического проводника представлена на рис.12.3
, T- термодинамическая температура; так что с ростом температуры сопротивление металлических проводников увеличивается. Качественная температурная зависимость удельного сопротивления металлического проводника представлена на рис.12.3
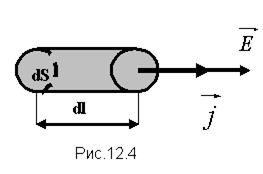
Найдем связь между векторами 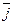 и
и 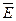 . Для этого мысленно выделим в окрестности некоторой точки проводника элементарный цилиндрический объем с образующими, параллельными векторам
. Для этого мысленно выделим в окрестности некоторой точки проводника элементарный цилиндрический объем с образующими, параллельными векторам 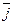 и
и 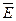 , (рис.12.4).
, (рис.12.4).
Между концами проводника длиной dl напряжение U = Edl, под действием которого через его поперечное сечение площадью dS течет ток I = jdS.
Сопротивление цилиндрического проводника, в нашем случае, равно
R = 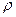
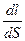 .
.
Используя закон Ома для участка цепи I = 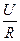 , находим:
, находим:
jdS = 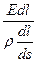 ,
,
откуда и получаем закон Ома в дифференциальной форме
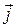 =
= 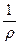
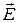 =
= 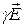 , (12-16)
, (12-16)
где 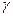 =
= 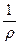 удельная электропроводность; [
удельная электропроводность; [ 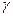 ] = 1 / (Ом м).
] = 1 / (Ом м).
Дата добавления: 2015-04-15; просмотров: 1182;
