Закон Ома для неоднородного участка цепи
На неоднородном участке цепи плотность тока пропорциональна сумме напряженностей электростатического поля и поля сторонних сил, т.е.
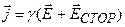 . (12-17)
. (12-17)
Рассмотрим цилиндрический проводник длиной l с площадью поперечного сечения S. Умножим обе части равенства (12-17) на перемещение dl вдоль оси проводника и проинтегрируем получившееся соотношение по длине проводника от 0 до l:
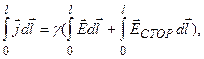
что дает
j× l = 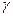 (
( 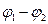 +
+ 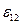 ). (12-18)
). (12-18)
Заменив j на I/S, а 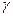 на
на 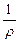 , из (12-18) получим I
, из (12-18) получим I 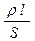 =
= 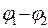 +
+ 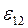 , откуда следует закон Ома для неоднородного участка цепи
, откуда следует закон Ома для неоднородного участка цепи
I = ( 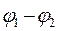 +
+ 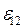 ) / R
) / R 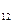 (12-19)
(12-19)
где R 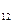 =
= 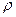 l / S - сопротивление участка цепи 12. Для замкнутой цепи
l / S - сопротивление участка цепи 12. Для замкнутой цепи 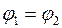 формула (12-19) запишется в виде
формула (12-19) запишется в виде
I = 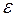 / R
/ R 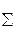 (12-20)
(12-20)
где R 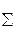 - суммарное сопротивление всей цепи;
- суммарное сопротивление всей цепи; 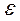 - ЭДС источника.
- ЭДС источника.
Пусть замкнутая цепь состоит из источника электрической энергии с ЭДС 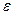 и внутренним сопротивлением r, а также внешней цепи потребителя, имеющей сопротивление R. Согласно (12-20)
и внутренним сопротивлением r, а также внешней цепи потребителя, имеющей сопротивление R. Согласно (12-20)
I = 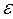 / (R + r). (12-21)
/ (R + r). (12-21)
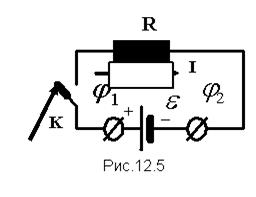
азность потенциалов на электродах источника, рис.12.5, равна напряжению на внешнем участке цепи:
U = 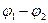 = IR =
= IR = 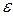 - Ir. (12-22)
- Ir. (12-22)
Если цепь разомкнуть, то ток в ней прекратится и напряжение U на зажимах источника станет равным его ЭДС, т.е. U = 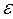 .
.
Таким образом, напряжение на внешнем участке цепи, будет равно
U = IR = 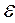 R / (R + r). (12-23)
R / (R + r). (12-23)
В пределе, когда R 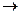 0 (источник тока замкнут накоротко), то в этом случае, в соответствии с (12-21), ток максимален
0 (источник тока замкнут накоротко), то в этом случае, в соответствии с (12-21), ток максимален
I 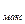 = I
= I 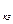 =
= 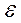 / R , (12-24)
/ R , (12-24)
а напряжение во внешней цепи равно нулю.
В противоположном предельном случае, R 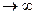 , цепь разомкнута и ток отсутствует: I=lim
, цепь разомкнута и ток отсутствует: I=lim 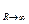 [
[ 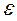 / (R+r)]=0, а напряжение на зажимах источника максимально и равно его ЭДС:
/ (R+r)]=0, а напряжение на зажимах источника максимально и равно его ЭДС:
U 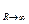 =
= 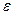 R / (R + r)=
R / (R + r)= 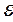 , т. к. lim
, т. к. lim 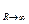 R / (R + r) = 1.(12-25)
R / (R + r) = 1.(12-25)
12.5. Закон Джоуля – Ленца. Работа и мощность тока.
Проводник нагревается, если по нему протекает электрический ток. Джоуль и Ленц установили, что количество выделившегося тепла
Q = I 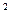 Rt, (12-26)
Rt, (12-26)
где I - ток, R - сопротивление, t - время протекания тока. Легко доказать, что
Q = I 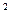 Rt = UIt = U 2 t/R = qU, (12-27)
Rt = UIt = U 2 t/R = qU, (12-27)
где q = It - электрический заряд.
Если ток изменяется со временем (т. е. в случае непостоянного тока), то
Q= 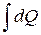 =
= 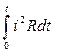 ,(12-28)
,(12-28)
где i - мгновенное значение тока.
Нагревание проводника происходит за счет работы, совершаемой силами электрического поля над носителями заряда. Эта работа
A=qU=UIt=I 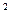 Rt = U
Rt = U 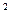 t / R . (12-29)
t / R . (12-29)
Работа А, энергия W , количество тепла Q в СИ измеряются в Дж.
Так как мощность характеризует работу, совершаемую в единицу времени, т.е. Р = 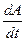 , то
, то
P=UI=I 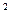 R=U
R=U 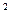 /R . (12-30)
/R . (12-30)
Мощность в СИ измеряется в ваттах: 1 Вт = 1 Дж / 1 с; откуда1 Дж = 1 Втс;
3600 Дж = 1Вт час, 3,6 •10 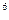 Дж = 1 кВт час.
Дж = 1 кВт час.
Формулы (12-29) и (12-30) позволяют рассчитать полезную работу и полезную мощность. Затраченная работа и мощность определяется по формулам
A 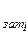 = q
= q 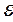 =
= 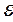 It = I
It = I  (R + r)t =
(R + r)t = 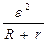 t. (12-31)
t. (12-31)
P 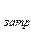 =
= 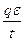 =
= 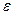 I = I
I = I 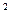 (R + r) =
(R + r) = 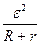 . (12-32)
. (12-32)
Отношение полезной работы (мощности) к затраченной характеризует КПД источника
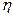 =
= 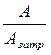 =
= 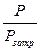 =
= 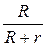 . (12-33)
. (12-33)
Из (12-33) следует, что при R®0,h®0; R®¥,h®1.Но при R 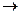
 ток I
ток I 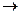 0 и поэтому А
0 и поэтому А 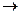 О и Р
О и Р 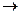 0.
0.
Определим величину R , при котором выделится максимальная мощность. Легко показать, что это наступает при R = r, тогда
PMAКС=I 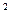 R =
R = 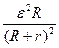 =
= 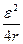 , (12-34)
, (12-34)
КПД в этом случае будет 50%.
Согласно закону Джоуля - Ленца в элементарном цилиндрическом объеме dV с площадью поперечного сечения dS и длиной dl за время dt выделится тепло
dQ =I 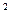 Rdt =(jdS)
Rdt =(jdS) 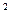
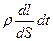 =
= 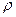 j
j 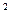 dldSdt =
dldSdt = 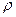 j
j 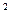 dVdt.
dVdt.
Разделив на dV и dt, найдем количество тепла, выделяющееся в единицу времени в единице объема
Q 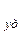 =
= 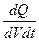 =
= 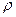 j
j 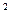 . (12-35)
. (12-35)
здесь Q 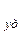 -называется удельной тепловой мощностью тока, которая в СИ измеряется в Вт/м3.
-называется удельной тепловой мощностью тока, которая в СИ измеряется в Вт/м3.
С учетом (12-16) из (12-3) следует, что
Q 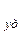 =
= 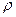 j
j 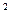 =
= 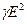 . (12-36)
. (12-36)
Формулы (12-35) и (12-36) выражают закон Джоуля - Ленца в дифференциальной форме.
Дата добавления: 2015-04-15; просмотров: 1164;
