Основные характеристики и закономерности агрегатных состояний и фазовых переходов.

Понятие фаза в термодинамике рассматривают в более широком смысле, чем агрегатные состояния. Под фазой в термодинамике понимают термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества. Иногда неравновесное метастабильное состояние вещества также называют фазой, но метастабильной. Фазы вещества могут отличаться характером движения структурных частиц и наличием или отсутствием упорядоченной структуры. Различные кристаллические фазы могут отличаться друг от друга типом кристаллической структуры, электропроводностью, электрическими и магнитными свойствами и др. Жидкие фазы отличаются друг от друга концентрацией компонентов, наличием или отсутствием сверхпроводимости и т.п.

Переход вещества из одной фазы в другую называется фазовым переходом. К фазовым переходам относятся явления парообразования и плавления, конденсации и кристаллизации и др.. В двухфазной системе фазы находятся в равновесии при одной и той же температуре. При увеличении объёма некоторая часть жидкости превращается в пар, но при этом для поддержания температуры неизменной необходимо извне передать некоторое количество теплоты. Таким образом, для осуществления перехода из жидкой фазы в газообразную системе необходимо передать теплоту без изменения температуры системы. Эта теплота идёт на изменение фазового состояния вещества и называется теплотой фазового превращения или скрытой теплотой перехода. С повышением температуры скрытая теплота перехода фиксированной массы вещества уменьшается, а при критической температуре она равна нулю. Для характеристики фазового перехода используют удельную теплоту фазового перехода. Удельной теплотой фазового перехода называется количество скрытой теплоты, приходящейся на единицу массы вещества.

Фазовые переходы с поглощением или выделением скрытой теплоты перехода называются фазовыми переходами первого рода. При этом внутренняя энергия и плотность изменяются скачком. При переходе из более упорядоченного состояния в менее упорядоченное состояние энтропия увеличивается. В таблице приведены фазовые переходы первого рода и их основные характеристики.

Таблица. Фазовые переходы первого рада и их основные характеристики.

Фазовый переход	Направление перехода	Скрытая теплота перехода	Изменение энтропии при фазовом переходе
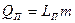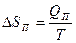Парообразование	Жидкость Þ пар	, где LП – удельная теплота парообразования, т- масса жидкости, переведённой в пар.	Энтропия возрастает ΔSП >0
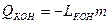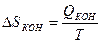Конденсация	Пар Þ жидкость	, где LКОН – величина удельной теплоты конденсации, т- масса пара, переведённого в жидкость	Энтропия убывает ΔSкр < 0
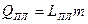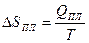Плавление	Твёрдое телоÞ жидкость	, где LПЛ – удельная теплота плавления, т- масса твёрдого тела, переведённого в жидкость	Энтропия возрастает ΔSпл > 0
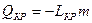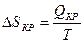Кристаллизация	Жидкость Þ твёрдое тело	, где LКР – величина удельной теплоты кристаллизации, т- масса жидкости, переведённой в твёрдое тело - кристалл	Энтропия убывает ΔSкр < 0
Сублимация (или возгонка)	Твёрдое тело Þ Пар	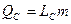, где LС – удельная теплота сублимации, т- масса твёрдого тела, переведённого в пар	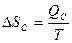Энтропия возрастает ΔSc > 0
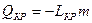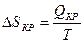Десублимация (Кристаллизация минуя жидкую фазу)	Пар Þ твёрдое тело (минуя жидкую фазу)	, где LКР – величина удельной теплоты кристаллизации, т- масса пара, переведённого в твёрдое тело - кристалл	Энтропия убывает ΔSкр < 0

Существует связь между давлением, при котором находится в равновесии двухфазная система, и температурой при фазовых переходах первого рода. Эта связь описывается уравнением Клапейрона – Клаузиуса. Рассмотрим вывод этого уравнения для закрытых систем. Если число частиц в системе постоянно, то изменение внутренней энергии, согласно первому началу термодинамики, определяется выражением: 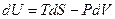. Равновесие между фазами наступит при условии, что Т₁ = Т₂ и Р₁ = Р₂ . Рассмотрим бесконечно малый обратимый цикл Карно (рис.6.8), изотермы которого соответствуют состоянию двухфазной системы при температурах Т и dT . Поскольку параметры состояния при этом изменяются бесконечно мало, изотермы и адиабаты на рис.10.2 изображены прямыми. Давление в таком цикле изменяется на величину dP . Работа системы за цикл определяется формулой: 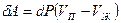. Предположим, что цикл реализован для системы масса вещества которой равна единице. Коэффициент полезного действия такого элементарного цикла Карно можно определить по формулам: 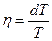или 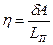, где L_П – удельная теплота парообразования. Приравнивая правые части этих равенств, и подставив выражение работы через давление и объём, получим: 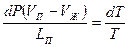. Соотнесём изменение давления с изменением температуры и получим:

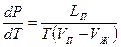(10-5)

Уравнение (10-5) называется уравнением Клапейрона – Клаузиуса. Анализируя это уравнение, можно заключить, что с ростом температуры давление увеличивается. Это следует из того, что 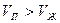, а значит и .

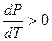Уравнение Клапейрона – Клаузиуса применимо не только к переходу «жидкость – пар». Оно применимо ко всем переходам первого рода. В общем виде его можно записать так:

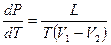(10-6)

Используя уравнение Клапейрона – Клаузиуса можно представить диаграмму состояний системы в координатах Р,Т (рис.10.3). На этой диаграмме кривая 1 – кривая сублимации. Она соответствует равновесному состоянию двух фаз: твёрдой и парообразной. Точки, лежащие слева от этой кривой характеризуют однофазное твёрдое состояние. Точки, лежащие справа, характеризуют парообразное состояние. Кривая 2 – кривая плавления. Она соответствует равновесному состоянию двух фаз: твёрдой и жидкой. Точки, лежащие слева от этой кривой характеризуют однофазное твёрдое состояние. Точки, лежащие справа от неё до кривой 3, характеризуют жидкое состояние. Кривая 3 – кривая парообразования. Она соответствует равновесному состоянию двух фаз: жидкой и парообразной. Точки, лежащие слева от этой кривой характеризуют однофазное жидкое состояние. Точки, лежащие справа, характеризуют парообразное состояние. Кривая 3, в отличии от кривых 1 и 2, ограничена с двух сторон. С одной стороны – тройной точкой Тр, с другой стороны - критической точкой К (рис.10.3). Тройная точка описывает равновесное состояние сразу трёх фаз: твёрдой, жидкой и парообразной.

Фазовые переходы второго рода. Жидкий гелий. Сверхтекучесть

Существуют фазовые переходы второго рода, при которых некоторые свойства вещества изменяются скачком. Характерной особенностью таких переходов является отсутствие теплоты перехода. К фазовым переходам второго рода относятся такие переходы как потеря ферромагнитных свойств при переходе через точку Кюри, переход проводника в сверхпроводящее состояние, переход гелия I в гелий II. Рассмотрим фазовый переход второго рода на примере жидкого гелия. Жидкий гелий замечателен тем, что это самая холодная жидкость в природе. Наиболее важной особенностью жидкого гелия является существование двух его модификаций, переходящих одна в другую при температуре 2,186 К при атмосферном давлении. Эти модификации называют Не-I и Не-II. Точка перехода Не-I в Не-II называется λ- точкой из-за вида кривой температурной зависимости теплоёмкости жидкого гелия, напоминающей букву λ (рис.10.4).

Переход Не-I в Не-II происходит без выделения или поглощения скрытой теплоты, что говорит о фазовом переходе второго рода. Свойства этих модификаций гелия различны. Не-I –бесцветная жидкость, бурно кипящая с обильным выделением пузырьков.( Не-II низкотемпературная модификация) - спокойная жидкость с отчётливой поверхностью, обладающая чрезвычайно

высокой теплопроводностью и сверхтекучестью. Сверхтекучесть Не-II открыл в 1938 году П.Л.Капица (нобелевский лауреат). Объяснение этого явления было дано в 1941 году Л.Д.Ландау на основе квантово-механических представлений о характере теплового движения в жидком гелии. Течение жидкого Не-II происходит так, как будто его вязкость равна нулю. Это значит, что он может свободно протекать через самые тонкие капилляры, щели, отверстия, непроницаемые даже для газов. В тонких капиллярах (диаметром 10^-4 ÷10^-5 см) течение жидкого Не-II уже не определяется уравнением Пуазейля и скорость течения его не зависит от разности давлений и длины капилляра. Однако, существует определённая критическая скорость, выше которой начинают действовать силы трения и движение становится вязким. Величина критической скорости повышается с понижением температуры и при самых низких температурах становится постоянной. На поверхности всякого твёрдого тела, соприкасающегося с жидким Не-II образуется тонкая движущаяся плёнка. Она движется в сторону, где температура выше. Если поверхность тела имеет одинаковую температуру, меньшую температуры λ- точки, и часть тела не погружена в жидкий гелий, то не погруженная часть поверхности покрывается тонкой плёнкой. В жидком Не-II наблюдается термомеханический эффект, который заключается в том, что, когда в тонком капилляре существует поток тепла, то в направлении, противоположном этому потоку, возникает поток жидкости.

Жидкий Не-II ещё и сверхтеплопроводен. Теплопроводность при переходе через λ- точку возрастает в 5 ^.10⁶ раз и становится лучше, чем у металлических проводников тепла.