Основной закон теплопроводности
Для распространения теплоты в любом теле или пространстве необходимо наличие разности температур в различных точках тела. Это условие относится и к передаче теплоты теплопроводностью, при которой температурный градиент в различных точках тела не должен быть равен нулю.
Связь между количеством теплоты dQ, проходящим через элементарную площадку dF, расположенную на изотермической поверхности, за промежуток времени dτ и температурным градиентом устанавливается гипотезой Фурье, согласно которой
 (22-6)
(22-6)
Минус в правой части показывает, что в направлении теплового потока температура убывает и величина grad t является величиной отрицательной. Множитель пропорциональности К называют коэффициентом теплопроводности. Уравнение (22-6) носит название основного уравнении теплопроводности, или закона Фурье. Справедливость гипотезы Фурье подтверждается опытами.
Количество теплоты, проходящей через единицу изотермической поверхности в единицу времени, называют плотностью, или вектором, теплового потока:
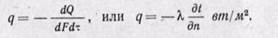 (22-7)
(22-7)
Вектор теплового потока направлен по нормали к изотермической поверхности в сторону убывания температуры. Векторы q и grad t лежат на одной прямой, по направлены в противоположные стороны.
Количество теплоты, прошедшей в единицу времени через изотермическую поверхность F, называют тепловым потоком:
 (22-8)
(22-8)
Количество теплоты, прошедшее за время т через изотермическую поверхность F конечных размеров, определяют из уравнения
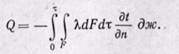 (22-9)
(22-9)
Таким образом, для определения количества теплоты, проходящей через какую-либо изотермическую поверхность твердого тела, необходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и составляет основную задачу аналитической теории теплопроводности.
Дата добавления: 2015-04-15; просмотров: 662;
