Температурный градиент

Если соединить точки тела с одинаковой температурой, то полу­чим поверхность равных температур, называемую изотермической. Изотермические поверхности между собой никогда не пересекаются.

Они либо замыкаются на себя, либо кон­чаются на границах тела.

Рассмотрим две близкие изотермические поверхности с температурами t и t + Δt (рис. 22-1). Перемещаясь из какой-либо точки А, можно обнаружить, что интенсив­ность изменения 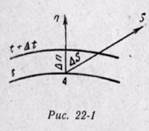температуры по различ­ным направлениям неодинакова. Если пе­ ремещаться по изотермической поверхно­сти, то изменения температуры не обна­ружим. Если же перемещаться вдоль какого-либо направления S, то будет наблюдаться изменение температуры. Наибольшую разность температур на единицу длины будем наблюдать в направлении нор­мали к изотермической поверхности. Предел отношения изменения температуры Δt к расстоянию между изотермами по нормали Δn, когда ан стремится к нулю, называют градиентом температуры:

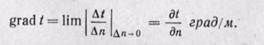(22-5)

Температурный градиент есть вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной от температуры по нормали п. За положительное направление градиента принимается направление возрастания температур.