СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ УСИЛИЯ В ТОЧКЕ ПОДВЕСА ШТАНГ
В процессе работы СК на его балансир действует три вида усилий: а) статические – масса штанг Р и жидкости G; б) динамические – усилие движущихся масс штанг Рi и жидкости Gi; в) трения – усилия от трения плунжера о цилиндр и штанг о трубы 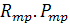 составляет 2-5% от величины статических сил.
составляет 2-5% от величины статических сил.
Общая величина сил рассчитывается по формуле:
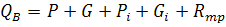 (63)
(63)
Рассмотрим и определим значения всех составляющих формулы (63).
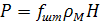 (64)
(64)
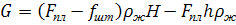 (65)
(65)
где 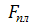 - площадь плунжера, м2;
- площадь плунжера, м2;
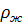 - плотность жидкости, кг/м3;
- плотность жидкости, кг/м3;
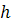 - глубина погружения насоса под динамический уровень, м;
- глубина погружения насоса под динамический уровень, м;
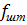 - площадь сечения штанг, м2;
- площадь сечения штанг, м2;
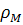 - плотность металла штанг, кг/м3;
- плотность металла штанг, кг/м3;
h0- динамический уровень, м;
Н- глубина подвеса насоса, м.
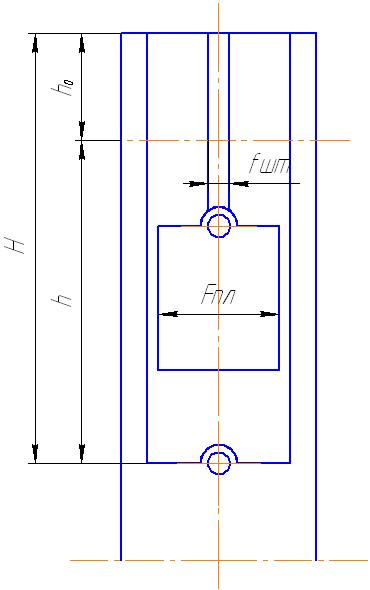
Рисунок 26- Схема подвеса насоса в скважине.
Величина статических сил 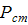 равна:
равна:
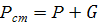 (66)
(66)
или
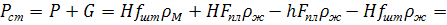
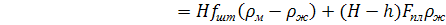 (67)
(67)
Преобразуем формулу (47), представив её в виде выражения:
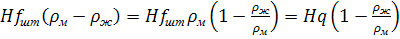 (68)
(68)
Результат обозначает массу штанг в жидкости с учетом потери их веса.
Выражение
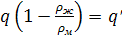 (69)
(69)
Есть масса единицы длины штанг в жидкости. Тогда формула (66) записывается:
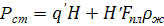 , (70)
, (70)
где H’=H-h – динамический уровень жидкости в скважине, м.
Как известно, сила инерции равна произведению массы на ускорение
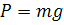 и
и 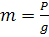
Для штанг получим
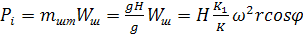 , (71)
, (71)
где 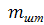 - масса штанг;
- масса штанг;
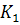 и К – плечи балансира;
и К – плечи балансира;
q- ускорение силы тяжести;
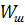 - ускорение точки подвеса штанг.
- ускорение точки подвеса штанг.
Силу инерции жидкости определяют с учетом различных площадей сечения столба жидкости в цилиндре насоса и трубах.
Для столба жидкости получим:
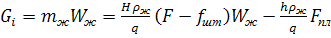 (72)
(72)
где 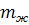 - масса столба жидкости в трубах;
- масса столба жидкости в трубах;
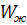 - ускорение столба жидкости в трубах.
- ускорение столба жидкости в трубах.
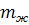 определена из формулы (67), в которой выражением
определена из формулы (67), в которой выражением 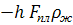 пренебрегли из-за его малости.
пренебрегли из-за его малости.
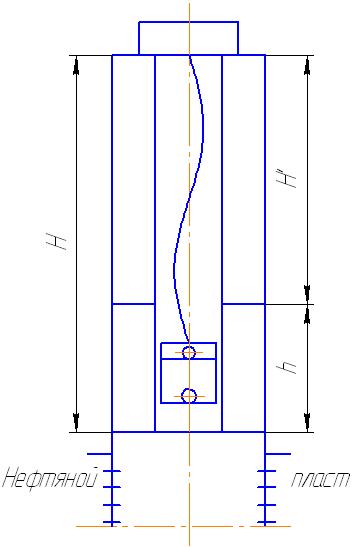
Рисунок 27-Схема изгиба штанговой колонны в скважине
Считаем, что жидкость движется безотрывно от штанг (условий безотрывности), т.е.
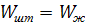 (73)
(73)
(справедливо для мелких скважин по элементарной теории расчета).
Тогда
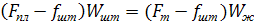 (74)
(74)
Из формулы (54):
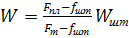 (75)
(75)
Обозначив
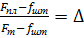 (76)
(76)
получим:
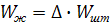 (77)
(77)
Максимальное значение силы инерции штанг и жидкости достигают при W=0, т.е. когда головка балансира начинает двигаться вверх от нижней мертвой точки.
Тогда
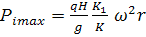 (78)
(78)
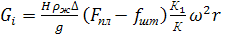 (79)
(79)
На самом деле, вследствие большой длины и упругости штанг и жидкости их массы приходят в движение не одновременно. При передаче нагрузки от труб штангам возникает колебательное движение, меняющее общую картину процесса.
Принимаем величину сил трения Rтр приближенно равной
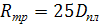 (80)
(80)
где Dпл – диаметр плунжера насоса, м.
Рассмотрим изменение сил при ходе вниз и вверх.
При ходе вниз G и Gi равны 0 и общая сила равна:
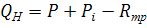 (81)
(81)
Найдем максимальную нагрузку на головку балансира из уравнения:
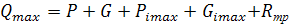 (82)
(82)
Из формулы (77) и (78):
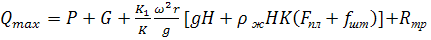 (83)
(83)
Произведем некоторые преобразования в формуле (82), имея в виду, что длина хода точки повеса штанг равна:
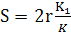 , и
, и 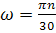
Получим:
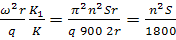 (84)
(84)
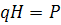 - масса колонны штанг без учета потерь массы в жидкости:
- масса колонны штанг без учета потерь массы в жидкости:
s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>G</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 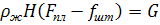 масса столба жидкости в кольцевом сечении.
масса столба жидкости в кольцевом сечении.
Обозначив массу колонны штаг с учетом потерь массы в жидкости, получим
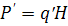 (85)
(85)
Масса столба жидкости в скважине от динамического уровня до устья равна
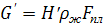 (86)
(86)
Формула для максимальной нагрузки примет вид:
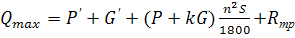 (87)
(87)
Величина Н, Н’, S – в м; Fпл, fшт – в см2.
А.Н. Адониным предложена формула:
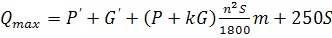 (88)
(88)
где m – кинематический показатель совершенства СК.
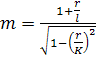
Дата добавления: 2015-04-15; просмотров: 1643;
