Расчеты по уточненной (приближенной) теории
В реальных условиях шатун имеет конечную длину и наше допущение относительно его бесконечности, позволяющее принять  и
и 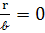 , становится ошибочным в СК с длиной хода от 3м и выше.
, становится ошибочным в СК с длиной хода от 3м и выше.
Уточненная теория так же пренебрегает кривизной движения точки «В» (движение точки «В» принимается по прямой В1ВВ2), но учитывает конечную длину шатуна.
Задача теории – установить более точные (по сравнению с элементарной ), приемлемые для практики формулы по определению пути, скорости, ускорения.
Из элементарной теории:
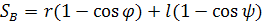
Из треугольника АОВ (рисунок 18) по теореме синусов:
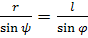 (34)
(34)
sin ψ = 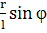 (35)
(35)
Зная sin ψ, можно определить cos ψ (sin2ψ+cos2ψ=1)
Из формулы (33), заменив sin φ на cos φ, получим:
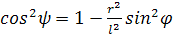 (36)
(36)
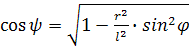 (37)
(37)
Руководствуясь правилом математики, принятом для малых величин
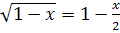 (38)
(38)
получим:
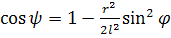 (39)
(39)
Подставляя значения  в формулу пути, получим
в формулу пути, получим
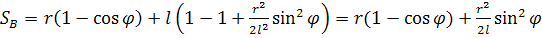 (40)
(40)
Путь 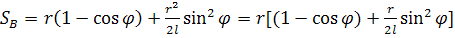 (41)
(41)
Первая производная этого выражения есть скорость
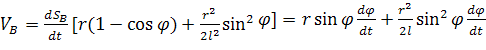 (42)
(42)
Вспомним, что
d cos=-sin; 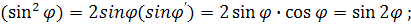
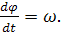
Тогда:
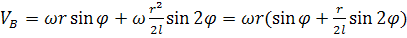 (43)
(43)
Ускорение найдем как производную от VB
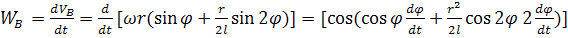 (42)
(42)
Вспомним, что 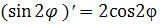
В окончательном виде формула ускорения:
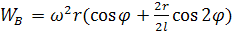 (44)
(44)
Очевидно, при равенстве плеч балансира движении точки «Д» идентично движению точки «В», а полученные формулы справедливы и для «Д».
В случае разновеликих плеч для точки «Д» в формулы следует вставить соотношение 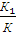 , т.е.
, т.е.
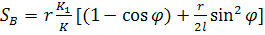 (45)
(45)
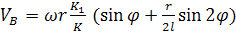 (46)
(46)
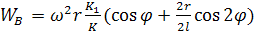 (47)
(47)
Максимальное значение пути, скорости, ускорения точки подвеса штанг соответственно опишутся следующими уравнениями:
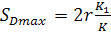 при 𝜑 =180
при 𝜑 =180 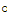 (48)
(48)
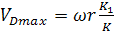 при 𝜑=90
при 𝜑=90 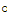 и
и 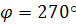 (49)
(49)
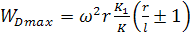 при 𝜑=0
при 𝜑=0 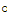 (50)
(50)
Графики ускорений по элементарной (2) и уточненной теории (1)представлены на рисунке 22.
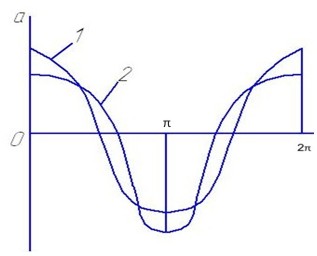
Рисунок 22- График ускорения по уточенной (1) и элементарной (2) теории.
Дата добавления: 2015-04-15; просмотров: 1072;
