Определение индексов общности
| а (число общих видов для двух списков) | b (число видов, имеющихся только во втором списке) | а + b (общее число видов во втором списке) |
| с (число видов, имеющихся только в первом списке) | d (число видов, отсутствующих в обоих списках, но имеющихся в других, в которые входит всего S видов) | с + d (число отсутствующих видов во втором списке) |
| а + с (общее число видов в первом списке) | b+d (число отсутствующих видов в первом списке) | a+b+c+d=S (всего видов) |
Сумма (а + d) называется числом совпадений качественных признаков; сумму (b + с) называют числом несовпадений; а – числом положительных и d – числом отрицательных совпадений.
Все известные индексы общности распадаются на две группы в зависимости от того, учитывают они или игнорируют число отрицательных совпадений (d). Наибольшее значение в экологических работах имеют индексы, в формулы которых входит только число положительных совпадений. В табл. 5.7.2 приведены основные индексы общности.
Предложено огромное число индексов общности, но чаще в биоценологических, фаунистических и биогеографических работах используются индексы Жаккара и Серенсена – Чекановского. Эти коэффициенты равны 1 в случае полного совпадения видов сообществ и равны 0, если выборки совершенно различны и не включают общих видов.
Индексы общности, учитывающие негативные совпадения, используются обычно при сравнении коллекций, когда известны полные видовые списки. Применение этой группы индексов в экологических и биогеографических исследованиях подвергалось серьезной критике. Ограниченное использование индексов, учитывающих отрицательные совпадения, связано с их большой зависимо стью от редких видов, которые могут не попадать в выборки.
Таблица 5.7.2
Основные индексы общности, учитывающие положительные совпадения [Песенко, 1982]
| Формула | Автор | Отношение |
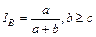
| Браун –Бланке, 1932 | а к числу видов в большем списке |
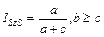
| Шимкевич,1926; Симпсон,1943 | а к числу видов в меньшем списке |
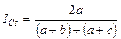
| Чекановский, 1900; Серенсен, 1948 | а к среднему арифметическому числу видов в двух списках |
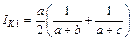
| Кульчинский, 1927 | а к среднему гармоническому числу видов в двух списках |
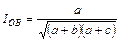
| Охайя,1957; Баркман,1958 | О к среднему геометрическому числу видов в двух списках |
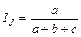
| Жаккар,1901 | а к. числу видов в объединенном списке |
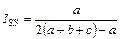
| Сокал, Снит, 1963 | а к сумме числа видов в объединенном списке и числу необщих видов |
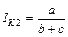
| Кульчинский, 1927 | а к числу необщих видов |
Объективные причины отсутствия были проанализированы Ю. А. Песенко [1982]. Отсутствие вида в сборах может быть результатом неподходящих условий для его существования в местах сборов, т.е. вид не может здесь жить, его ниши нет в данной местности. Вследствие некоторых исторических (географических) причин эволюция вида проходила в отдаленных от этих мест регионах, т.е. он не мог сюда попасть, хотя в данной местности и имелись подходящие для него условия. Вид может существовать в данной местности, но не попал в выборку из-за неадекватности методов сбора, или из-за редкости вида. Отсутствие вида как результат первых двух причин несет ценную информацию о фауне и местообитании, но только при исключении третьей причины, что сделать, как правило, невозможно.
Наиболее распространенными из индексов, учитывающих отрицательные совпадения, являются коэффициент простого совпадения или индекс Сокала – Майченера.
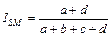
и индекс общности Барони – Урбани и Бюссера:
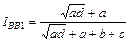 ,
, 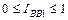
Проблема оценки достоверности этих индексов не решена. Простота вычисления, являющаяся достоинством многих индексов, оборачивается недостатком – они не включают обилие видов. Это обстоятельство привело к тому, что чаще используются модифицированные индексы, включающие оценку обилий.
Дата добавления: 2015-04-11; просмотров: 1894;
