Фазовые переходы

На простом примере можно убедиться, что свойства сети критическим образом зависят от температуры . Действительно, если величины всех синаптических связей положительны и равны между собой: (такая система эквивалентна ферромагнетику), то все уравнения системы сводятся к одному

.

Решение этого уравнения зависит от крутизны наклона функции гиперболического тангенса в начале координат. При высокой температуре уравнение имеет только тривиальное решение . Это означает, что состояния всех нейронов беспорядочно флуктуируют, принимая с равной вероятностью значения .

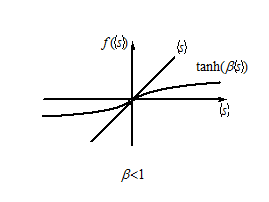
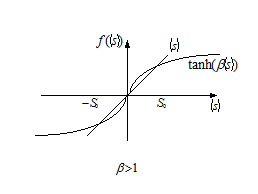
Рис. 11.5. Иллюстрация к характеру решений уравнения среднего поля в приближении высокой и низкой температур

Однако, при снижении температуры ниже точки Кюри в системе происходит фазовый переход, при котором тривиальное решение становится неустойчивым, а у уравнения среднего поля появляется еще два устойчивых нетривиальных решения .

Такое поведение характерно и для общего случая. Мы увидим далее, что в модели Хопфилда свойства ассоциативного запоминания и вызова образов проявляются в некоторой области температуры и дополнительного параметра - степени загрузки памяти. Вне этой области система переходит в неупорядоченное состояние.