Элементы нечеткой логики

Центральным понятием нечеткой логики является понятие лингвистической переменной. Согласно Лотфи Заде лингвистической называется переменная, значениями которой являются слова или предложения естественного или искусственного языка. Примером лингвистической переменной является, например, падение производства, если она принимает не числовые, а лингвистические значения, такие как, например, незначительное, заметное, существенное, и катастрофическое. Очевидно, что лингвистические значения нечетко характеризуют имеющуюся ситуацию. Например, падение производства на 3% можно рассматривать и как в какой-то мере незначительное, и как в какой-то мере заметное.Интуитивно ясно, что мера того, что данное падение является катастрофическим, должна быть весьма мала.

Смысл лингвистического значения X и характеризуется выбранной мерой - так называемой функций принадлежности (membership function) , которая каждому элементу u универсального множества U ставит в соответствие значение совместимости этого элемента с X . В нашем случае универсальным множеством является множество всех возможных величин падения производства (от 0 до 100%).

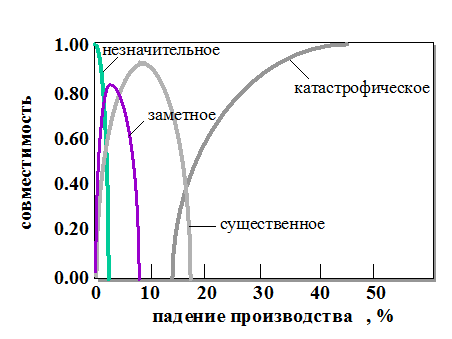
Рис. 11.2. Функции принадлежности лингвистической переменной Падение производства

Нечеткое правило связывает значения лингвистических переменных. Примером такого правила может быть, например, следующее.

Если (падение производства - катастрофическое), то (доходы от экспорта энергоресурсов-значительные).

Нечеткое подмножество универсального множества U характеризуется функцией принадлежности , которая ставит в соответствие каждому элементу число из интервала [0, 1], характеризующее степень принадлежности элемента u подмножеству A.

Носителем множества A называется множество таких точек в U, для которых величина положительна.