Извлечение правил if-then

В главе, посвященной извлечению знаний, мы уже познакомились с нейросетевыми методами извлечения правил из данных. Настало время узнать, как можно извлечь с их помощью нечеткие правила.

Рассмотрим набор нечетких правил

Если x есть A_i ,то y есть B_i ,

Каждое из них может интерпретироваться как обучающая пара для многослойного персептрона. При этом, условие (x есть A_i) определяет значение входа, а следствие (y есть B_i) - значение выхода сети. Полное обучающее множество имеет вид . Заметим, что каждому лингвистическому значению A_i, B_i соответствует своя функция принадлежности, так что каждое нечеткое правило определяет связь двух функций.

Если же правила имеют более сложный вид, типа “два входа - один выход”:

Если x есть A_i и y есть B_i , то z есть C_i ,

то обучающая выборка принимает форму ,

Существует два основных подхода к реализации нечетких правил типа if-then с помощью многослойных персептронов.

В методе Умано и Изавы нечеткое множество представляется конечным числом значений совместимости. Пусть включает носители всех , входящих в обучающую выборку, а также носители всех , которые могут быть входами в сети. Предположим также, что включает носители всех , входящих в обучающую выборку, а также носители всех , которые могут быть входами в сети. Положим

Дискретный аналог обучающего множества правил (заменяющее функциональное) имеет вид:

Если теперь ввести обозначения , то можно представить нечеткую нейронную сеть с входными ивыходными нейронами.

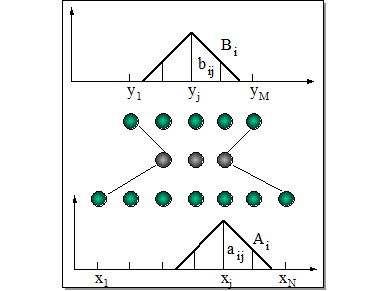
Рис. 11.3. Нечеткая нейронная сеть и треугольные функции принадлежности входных и выходных переменных

Пример 1. Предположим, что обучающая выборка включает три правила:

Если город мал, то доход от продажи бриллиантов отрицателен,

Если город средний, то доход от продажи бриллиантов близок к нулю,

Если город велик, то доход от продажи бриллиантов положителен.

Функции принадлежности определим как

(Здесь предполагается, что доход не превышает 100% или 1.0 в относительных величинах)

Тогда обучающая выборка принимает форму

{(малый, отрицательный), (средний, близок к нулю), (большой, положительный)}

Если носитель множества входов [0, 10 000 000], то для покрытия множества населения городов равномерной сеткой, захватывающей и малые города, понадобится несколько сот точек. Поэтому, ограничимся городами с населением 1 000 000 человек. Тогда можно выбрать . Носитель множества выходов [-1,1] может быть описан набором из . Таким образом, в рассматриваемом случае сеть будет иметь умеренные размеры (например 50 - ... - 5) и 3 пары в обучающем наборе.

В методе Уехары и Фуджицывместо разбиения равномерной сеткой области, покрывающей носители всех функций принадлежности, равномерно разбивается область изменения этих функций [0,1]. Здесь видна явная аналогия с переходом от интегрирования по Риману к интегралу Лебега. Остальные действия аналогичны уже описанным.