Выбор функционала ошибки
Если принять, что целью предсказаний финансовых временных рядов является максимизация прибыли, логично настраивать нейросеть именно на этот конечный результат. Например, при игре по описанной выше схеме для обучения нейросети можно выбрать следующую функцию ошибки обучения, усредненную по всем примерам из обучающей выборки:
.
Здесь доля капитала в игре введена в качестве дополнительного выхода сети, настраиваемого в процессе обучения. При таком подходе, первый нейрон, , с функцией активации даст вероятность возрастания или убывания курса, в то время как второй выход сети даст рекомендованную долю капитала в игре на данном шаге.
Поскольку, однако, в соответствии с предыдущим анализом, эта доля должна быть пропорциональна степени уверености предсказания, можно заменить два выхода сети - одним, положив , и ограничиться оптимизацией всего одного глобального параметра минимизирующего ошибку:
Тем самым, появляется возможность регулировать ставку в соответствии с уровнем риска, предсказываемым сетью. Игра с переменными ставками приносит большую прибыль, чем игра с фиксированными ставками. Действительно, если зафиксировать ставку, определив ее по средней предсказуемости, то скорость роста капитала будет пропорциональна , тогда как если определять оптимальную ставку на каждом шаге, то - пропорциональна .
Использование комитетов сетей
Из-за случайности в выборе начальных значений синаптических весов, предсказания сетей, обученных на одной и той же выборке, будут, вообще говоря, разниться. Этот недостаток (элемент неопределенности) можно превратить в достоинство, организовав комитет нейро-экспертов, состоящий из различных нейросетей. Разброс в предсказаниях экспертов даст представление о степени уверенности этих предсказаний, что можно использовать для правильного выбора стратегии игры.
Легко показать, что среднее значений комитета должно давать лучшие предсказания, чем средний эксперт из этого же комитета. Пусть ошибка -ого эксперта для значения входа равна . Средняя ошибка комитета всегда меньше среднеквадратичной ошибки отдельных экспертов в силу неравенства Коши:
Причем, снижение ошибки может быть довольно заметным. Так, если ошибки отдельных экспертов не коррелируют друг с другом, т.е. , то среднеквадратичная ошибка комитета из экспертов в раз меньше, чем среняя индивидуальная ошибка одного эксперта!
Поэтому, в предсказаниях всегда лучше опираться на средние значения всего комитета. Иллюстрацией этого факта служит Рисунок 20.
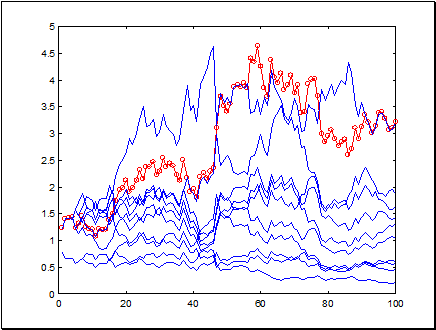
Рисунок 20. Норма прибыли на последних 100 значениях ряда sp500 при предсказании комитетом из 10 сетей. Выигрыш комитета (кружки) выше, чем выигрыш среднего эксперта. Счет угаданных знаков для комитета 59:41
Как видно из приведенного выше рисунка, в данном случае выигрыш комитета даже выше, чем выигрыш каждого из экспертов. Таким образом, метод комитетов может существенно повысить качество прогнозирования. Обратите внимание на абсолютное значение нормы прибыли: капитал комитета возрос в 3.25 раза при 100 вхождениях в рынок (Естественно, эта норма будет ниже при учете транзакционных издержек).
Предсказания получены при обучении сети на 30 последовательных экспоненциальных скользящих средних (EMA1 … EMA30) ряда приращений индекса. Предсказывался знак приращения на следующем шаге.
В этом эксперименте ставка была зафиксирована на уровне , близком к оптимальному при данной точности предсказаний (59 угаданных знаков против 41 ошибки) т.е. . На следующем же рисунке приведены результаты более рискованной игры по тем же предсказаниям, а именно - с .
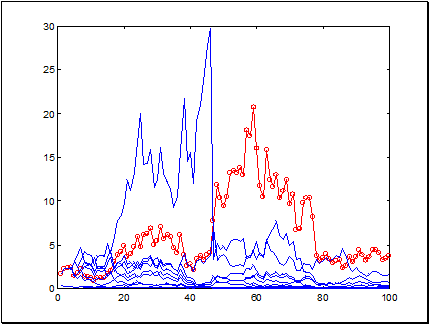
Рисунок Норма прибыли на последних 100 значениях ряда sp500 при тех же предсказаниях комитета из 10 сетей, но по более рискованной стратегии
Выигрыш комитета в целом остался на прежнем уровне (чуть увеличился), поскольку данное значение риска так же близко к оптимуму, как и предыдущее. Однако, для большинства сетей, предсказания которых хуже, чем у комитета в целом, такие ставки оказались слишком рискованными, что привело к практически полному их разорению.
Приведенные выше примеры показывают как важно уметь правильно оценить качество предсказания и как можно использовать эту оценку для увеличения прибыльности от одних и тех же предсказаний.
Можно пойти еще дальше и вместо среднего использовать взвешенное мнение сетей-экспертов. Веса выбираются адаптивно максимизируя предсказательную способность комитета на обучающей выборке. В итоге, хуже обученные сети из комитета вносят меньший вклад и не портят предсказания.
Возможности этого пути иллюстрирует приведенное ниже сравнение предсказаний двух типов комитетов из 25 экспертов (см. Рисунок 21 и Рисунок 22). Предсказания проводились по одной и той же схеме: в качестве входов использовались экспоненциальные скользящие средние приращений ряда с периодами равными первым 10 числам Фибоначчи. По результатам 100 экспериментов взвешенное предсказание дает в среднем превышение правильно угаданных знаков над ошибочным равное примерно 15, тогда как среднее - около 12. Заметим, что общее число повышений курса над понижением за указанный период как раз равно 12. Следовательно, учет общей тенденции к повышению в виде тривиального постоянного предсказания знака "+" дает такой же результат для процента угаданных знаков, что и взвешенное мнение 25 экспертов.
| 
|
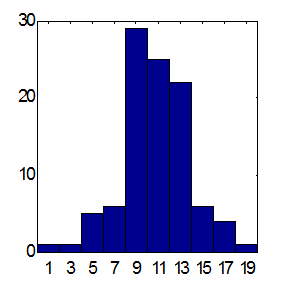
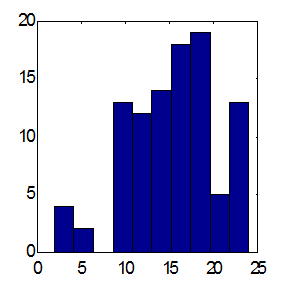
| Рисунок 21. Гистограмма сумм угаданных знаков при средних предсказаниях 25 экспертов. Среднее по 100 комитетам = 11.7 при стандартном отклонении 3.2 | Рисунок 22. Гистограмма сумм угаданных знаков при взвешенных предсказаниях тех же 25 экспертов. Среднее по 100 комитетам = 15.2 при стандартном отклонении 4.9 |
Возможная норма прибыли нейросетевых предсказаний
До сих пор результаты численных экспериментов формулировались нами в виде процента угаданных знаков. Зададимся теперь вопросом о реально достижимой норме прибыли при игре с помощью нейросетей. Полученные выше без учета влияния флуктуаций верхние границы нормы прибыли вряд ли достижимы на практике, тем более, что до сих пор мы не учитывали транзакционных издержек, которые могут свести на нет достигнутую степень предсказуемости.
Действительно, учет комиссионных приводит к появлению отрицательного члена в показателе экспоненты:
.
Причем, в отличае от степени предсказуемости , комиссия входит не квадратично, а линейно. Так, в приведенном выше примере типичные значения предсказуемости не смогут "пересилить" комиссию свыше.
Чтобы дать читателю представление о реальных возможностях нейросей в этой области, приведем результаты автоматического неросетевого трейдинга на трех финансовых инструментах, с различными характерными временами: значения индекса S$P500 с месячными интервалами между отсчетами, дневные котировки немецкой марки DM/$ и часовые отсчеты фьючерсов на акции Лукойл на Российской бирже. Статистика предсказаний набиралась на 50 различных нейросистемах (содержащих комитеты из 50 нейросетей каждая). Сами ряды и результаты по предсказанию знаков на тестовой выборке из 100 последних значений каждого ряда приведены на следующем рисунке.
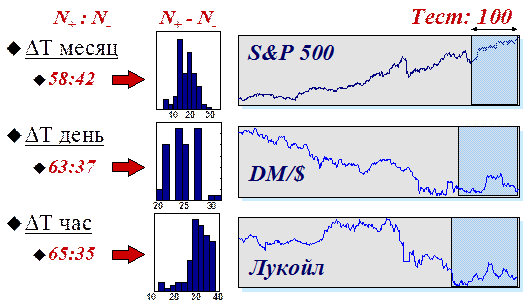
Рисунок 23. Средние значения и гистограммы количества правильно () и неправильно () угаданных знаков на тестовых выборках из 100 значений трех реальных финансовых инструментов.Эти результаты подтверждают интуитивно понятную закономерность: ряды тем более предсказуемы, чем меньше времени проходит между его отсчетами. Действительно, чем больше временной масштаб между последовательными значениями ряда, тем больше внешней по отношению к его динамике информации доступно участникам рынка, и, соответственно меньше информации о будущем содержится в самом ряде.
Далее полученные выше предсказания использовались для игры на тестовой выборке. При этом, размер контракта на каждом шаге выбирался пропорциональным степени уверенности предсказания, а значение глобального параметра оптимизировалось по обучающей выборке. Кроме того, в зависимости от своих успехов, каждая сеть в комитете имела свой плавающий рейтинг, и в предсказаниях на каждом шаге использовалась лишь "лучшая" в данный момент половина сетей. Результаты таких нейро-трейдеров показаны на следующем рисунке (Рисунок 24).
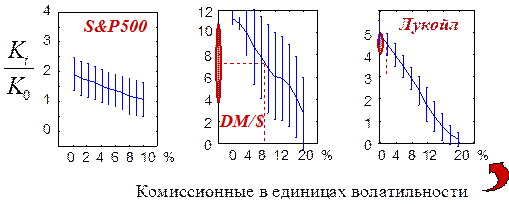
Рисунок 24 Статистика выигрышей по 50 реализациям в зависимости от величины комиссионных. Реалистичные значения комиссионных, показанные пунктиром, определяют область реально достижимых норм прибыли
Итоговый выигрыш (как и сама стратегия игры), естественно, зависит от величины комиссионных. Эта зависимость и изображена приведенных выше графиках. Там, где реалистичные значения комиссионных в выбранных единицах измерений были известны авторам, они отмечены на рисунке. Уточним, что в этих экспериментах не учитывалась "квантованность" реальной игры, т.е. то, что величина сделок должна равняться целому числу типовых контрактов. Этот случай соответствует игре на большом капитале, когда типичные сделки содержат много контрактов. Кроме того, подразумевалась залоговая форма игры, т.е. норма прибыли исчислялась к залоговому капиталу, гораздо меньшему, чем масштабы самих контрактов.
Приведенные выше результаты свидетельствуют о перспективности нейросетевого трейдинга, по крайней мере на "коротких" временных масштабах. Более того, в силу самоподобия финансовых временных рядов (Peters, 1994), норма прибыли за единицу времени будет тем выше, чем меньше характерное время трейдинга. Таким образом, автоматические нейросетевые трейдеры оказываются наиболее эффективны при торговле в реальном времени, где как раз наиболее заметны их преимущества над обычными брокерами: неутомляемость, неподверженность эмоциям, потенциально гораздо более высокая скорость реагирования. Обученная нейросеть, подсоединенная к электронной системе торгов, может принимать решения еще до того, как брокер-человек успеет распознать изменения графика котировок на своем терминале.
Заключение
Подытожим результаты этой главы. Во-первых, мы показали, что (по крайней мере, некоторые) рыночные временные ряды частично предсказуемы. Как и любой другой вид нейроанализа, предсказание временных рядов требует достаточно сложной и тщательной предобработки данных. Однако работа с временными рядами имеет свою специфику, которую можно использовать для увеличения прибыли. Это касается как выбора входов (использование специальных способов представления данных), так и выбора выходов и использования специфических функционалов ошибки. Наконец, мы показали, насколько выгоднее может быть использование комитетов нейро-экспертов по сравнению с отдельными нейросетями, и представили данные о реальных нормах прибыли на нескольких реальных финансовых инструментах.
Шарп, У.Ф., Александер Г.Дж., Бэйли, Дж. В. (1997). Инвестиции. Инфра-М.
Abu-Mostafa, Y.S. (1995). "Financial market applications of learning from hints”. In Neural Networks in Capital Markets. Apostolos-Paul Refenes (Ed.), Wiley, 221-232.
Beltratti, A., Margarita, S., and Terna, P. (1995). Neural Networks for Economic and Financial Modeling. ITCP.
Chorafas, D.N. (1994). Chaos Theory in the Financial Markets. Probus Publishing.
Colby, R.W., Meyers, T.A. (1988). The Encyclopedia of Technical Market Indicators. IRWIN Professional Publishing.
Ehlers, J.F. (1992). MESA and Trading Market Cycles. Wiley.
Kaiser, G. (1995). A Friendly Guide to Wavelets. Birk.
LeBeau, C., and Lucas, D.W. (1992). Technical traders guide to computer analysis of futures market. Business One Irwin.
Peters, E.E. (1994). Fractal Market Analysis. Wiley.
Pring, M.G. (1991). Technical Analysis Explained. McGraw Hill.
Plummer, T. (1989). Forecasting Financial Markets. Kogan Page.
Sauer, T., Yorke, J.A., and Casdagli, M. (1991). "Embedology". Journal of Statistical Physics. 65, 579-616.
Vemuri, V.R., and Rogers, R.D., eds. (1993). Artificial Neural Networks. Forecasting Time Series. IEEE Comp.Soc.Press.
Weigend, A and Gershenfield, eds. (1994). Times series prediction: Forecasting the future and understanding the past. Addison-Wesley.
Бэстенс, Д.-Э., Ван Ден Берг, В.-М., Вуд, Д. (1997). Нейронные сети и финансовые рынки. Принятие решений в торговых операциях. ТВП Научное издательство.
Извлечение знаний с помощью нейронных сетей
Искусственный интеллект, экспертные системы и нейронные сети. Извлечение правил из нейронных сетей. Алгоритм NeuroRule. Прореживание нейронных сетей. Обучение нейронных сетей с одновременным исправлением данных. Алгоритм TREPAN для извлечения деревьев решений с использованием нейронных сетей.
& Ковбойский язык очень легко понять, - заметил один ковбой. - Нужно просто заранее знать, что хочет сказать твой собеседник, и не обращать внимание на его слова.
Д.Бурстин, Американцы: демократический опыт
До сих пор нейросети рассматривались нами лишь как инструмент предсказания, но не понимания. Действительно, классический нейросетевой подход - метод черного ящика - предполагает создание имитационной модели, без явной формулировки правил принятия решений нейросетью. Вернее, эти правила содержатся в весах обученной нейросети, но понять их, переформулировав на язык “если… - то…” не представлялось возможным. В этой главе мы продемонстрируем методику, позволяющую строить подобные правила, объясняющие нейросетевые решения. Нейросети, таким образом, можно использовать не только для предсказаний, но и для извлечения знаний из баз данных.
Традиционно построение правил вывода и баз знаний считается прерогативой экспертных систем - направления искусственного интеллекта, которое претендовало в начале семидесятых годов заменить собою искусственные нейронные сети в задачах обработки информации. Экспертные системы были ориентированы именно на обработку данных с помощью некоторых правил вывода, которые предполагалось извлекать у экспертов в той или иной области знаний. Экспертные системы были призваны реализовывать цепочки рассуждений, имитирующих анализ ситуации экспертом-человеком. По сути в 70-е годы сам термин “искусственный интеллект” был синонимом разработки экспертных систем, или инженерии знаний.
Это направление, однако, столкнулось с рядом принципиальных трудностей. В частности, инженеры знаний должны были извлекать их у очень квалифицированных экспертов, которые, вообще говоря, не стремились поделиться информацией. Знания - большая ценность, и передавать их, чтобы помочь создать себе легко тиражируемую замену и, в конечном счете, обесценить себя как специалиста, стремился далеко не каждый. Но даже и при наличии соответствующего желания, эксперт не всегда мог внятно сформулировать те правила, которыми он пользуется при подготовке экспертного заключения. Очень многое в его работе связано с интуитивными качественными оценками, распознаванием ситуации в целом, то есть с не формализуемыми процедурами (мы знаем, что это как раз та ситуация, в которой особенно отчетливо проявляются преимущества нейросетевого подхода). Но даже если все трудности оказывались преодоленными, достоинства построенной экспертной системы оказывались не абсолютными, поскольку именно явная формализация правил вывода, а не компьютерная система сама по себе представляла основную ценность. В этом смысле весьма показателен опыт создания в 70-е годы в Стэнфордском университете экспертной системы MYCIN, с помощью которой врачи должны были повысить надежность диагностики септического шока. Септический шок, дававший в случае развития 50% летальных исходов у прооперированных больных вовремя диагностировался врачами лишь в половине случаев. Экспертная система MYCIN позволила повысить качество диагностики почти до 100%. Однако, после того, как врачи познакомились с ее работой, они очень быстро сами научились правильно ставить соответствующий диагноз. Необходимость в MYCIN отпала и она превратилась в учебную систему. Таким образом, основная польза проекта состояла именно в извлечении знаний в понятном для человека виде.
По мнению Стаббса, известного американского специалиста в области нейросетевых приложений, экспертные системы “пошли” только в кардиологии. Они эффективно заменили объемистые руководства по анализу электрокардиограмм, содержащие множество достаточно ясно сформулированных правил оценки их многообразных особенностей.
Нейронные сети выглядят предпочтительнее экспертных систем, позволяя одновременно анализировать множество в общем случае неточных и неполных параметров и не требуя при этом явной формализации правил вывода. Однако, объяснение тех или иных рекомендаций, полученных с помощью нейросетевого анализа, является требованием, которое обычно предъявляют специалисты, желающие использовать нейросетевые технологии. На первый взгляд здесь-то и находится их слабое место. Действительно, в такой области обработки информации, как извлечение знаний, нейронные сети стали применяться только относительно недавно. Это еще одна сфера, в которой доселе господствовал только традиционный искусственный интеллект. Рассмотрим ее более подробно.
Извлечение знаний
В последние годы созданы огромные базы данных, в которых хранится информация научного, экономического, делового и политического характера. В качестве примера можно привести GenBank, содержащий террабайты данных о последовательностях ДНК живых организмов. Для работы с подобными базами разработаны компьютерные технологии, позволяющие хранить, сортировать и визуализировать данные, осуществлять быстрый доступ к ним, осуществлять их статистическую обработку. Значительно меньшими являются, однако, достижения в разработке методов и программ, способных обнаружить в данных важную, но скрытую информацию. Можно сказать, что информация находится к данным в таком же отношении, как чистое золото к бедной золотоносной руде. Извлечение этой информации может дать критический толчок в бизнесе, в научных исследованиях и других областях. Подобное нетривиальное извлечение неявной, прежде неизвестной и потенциально полезной информации из больших баз данных и называется Разработкой Данных (Data Mining) или же Открытием Знаний (Knowledge Discovery). Мы будем использовать далее для описания этой области информатики более явный синтетический термин - извлечение знаний. Извлечение знаний использует концепции, разработанные в таких областях как машинное обучение (Machine Learning), технология баз данных (Database Technology), статистика и других.
Главными требованиями, предъявляемыми к методам извлечения знаний, являются эффективность и масштабируемость. Работа с очень большими базами данных требует эффективности алгоритмов, а неточность и, зачастую, неполнота данных порождают дополнительные проблемы для извлечения знаний. Нейронные сети имеют здесь неоспоримое преимущество, поскольку именно они являются наиболее эффективным средством работы с зашумленными данными. Действительно, заполнение пропусков в базах данных - одна из прототипических задач, решаемых нейросетями. Однако, главной претензией к нейронным сетям всегда было отсутствие объяснения. Демонстрация того, что нейронные сети действительно можно использовать для получения наглядно сформулированных правил было важным событием конца 80-х годов. В 1989 году один из авторов настоящего курса поинтересовался у Роберта Хехт-Нильсена, главы одной из наиболее известных американских нейрокомпьютерных фирм Hecht-Nielsen Neurocomputers, где можно узнать подробности о нейроэкспертных системах, информация о которых тогда носила только рекламный характер. Хехт-Нильсен ответил в том смысле, что она не доступна. Но уже через 2-3 месяца после этого в журнале Artificial Intelligence Expert была опубликована информация о том, что после долгих и трудных переговоров Хехт-Нильсен и крупнейший авторитет в области экспертных систем Гэллант запатентовали метод извлечения правил из обученных нейронных сетей и метод автоматической нейросетевой генерации экспертных систем.
Извлечение правил из нейронных сетей подразумевает их предварительное обучение. Поскольку эта процедура требует много времени для больших баз данных, то естественна та критика, которой подвергается использование нейротехнологии для извлечения знаний. Другим поводом для такой критики является трудность инкорпорации в нейронные сети некоторых имеющихся априорных знаний. Тем не менее, главным является артикуляция правил на основе анализа структуры нейронной сети. Если эта задача решается, то низкая ошибка классификации и робастность нейронных сетей дают им преимущества перед другими методами извлечения знаний.
Извлечение правил из нейронных сетей
Рассмотрим один из методов извлечения правил из нейронных сетей, обученных решению задачи классификации (Lu, Setiono and Liu, 1995). Этот метод носит название NeuroRule.
Задача состоит в классификации некоторого набора данных с помощью многослойного персептрона и последующего анализа полученной сети с целью нахождения классифицирующих правил, описывающих каждый из классов.
Пусть обозначает набор из N свойств , а - множество возможных значений, которое может принимать свойство . Обозначим через С множество классов . Для обучающей выборки известны ассоциированные пары векторов входных и выходных значений , где .
Алгоритм извлечения классифицирующих правил включает три этапа:
1. Обучение нейронной сети. На этом первом шаге двухслойный персептрон тренируется на обучающем наборе вплоть до получения достаточной точности классификации.
2. Прореживание (pruning) нейронной сети. Обученная нейронная сеть содержит все возможные связи между входными нейронами и нейронами скрытого слоя, а также между последними и выходными нейронами. Полное число этих связей обычно столь велико, что из анализа их значений невозможно извлечь обозримые для пользователя классифицирующие правила. Прореживание заключается в удалении излишних связей и нейронов, не приводящем к увеличению ошибки классификации сетью. Результирующая сеть обычно содержит немного нейронов и связей между ними и ее функционирование поддается исследованию.
3. Извлечение правил. На этом этапе из прореженной нейронной сети извлекаются правила, имеющие форму если () и () и ... и (), то , где - константы, - оператор отношения (). Предполагается, что эти правила достаточно очевидны при проверке и легко применяются к большим базам данных.
Рассмотрим все эти шаги более подробно
Дата добавления: 2015-04-10; просмотров: 1573;
