Обучение нейронной сети

Предположим, что обучающий набор данных необходимо расклассифицировать на два класса A и B. В этом случае сеть должна содержать N входных и 2 выходных нейрона. Каждому из классов будут соответствовать следующие активности выходных нейронов (1,0) и (0,1). Подходящее количество нейронов в промежуточном слое, вообще говоря, невозможно определить заранее - слишком большое их число ведет к переобучению, в то время как малое не обеспечивает достаточной точности обучения. Тем не мене, как уже отмечалось ранее, все методы адаптивного поиска числа нейронов в промежуточном слое делятся на два класса, в соответствии с тем, с малого или большого числа промежуточных нейронов стартует алгоритм. В первом случае по мере обучения в сеть добавляются дополнительные нейроны, в противоположном - после обучения происходит уничтожение излишних нейронов и связей. NeuroRuleиспользует последний подход, так что число промежуточных нейронов выбирается достаточно большим. Заметим, что NeuroRuleуничтожает также и избыточные входные нейроны, влияние которых на классификацию мало.

В качестве функции активации промежуточных нейронов используется гиперболический тангенс, так что их состояния изменяются в интервале [-1,1]. В то же время, функцией активации выходных нейронов является функция Ферми (состояния в интервале [0,1]). Обозначим через - состояния выходных нейронов при предъявлении на вход сети вектора признаков -го объекта . Будем считать, что этот объект правильно классифицирован сетью, если

,

где: если и если , а . В остальных случаях .

Минимизируемая функция ошибки должна не только направлять процесс обучения в сторону правильной классификации всех объектов обучающей выборки, но и делать малыми значения многих связей в сети, чтобы облегчить процесс их прореживания. Подобную технологию - путем добавления к функции ошибки специально подобранных штрафных членов - мы уже разбирали в Главе 3. В методе NeuroRuleфункция ошибка включает два слагаемых

,

где

функция взаимной энтропии, минимизация которой происходит быстрее, чем минимизация среднеквадратичной ошибки. Штрафная функция

уже фигурировала в лекции 3.

Здесь 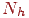- число нейронов в скрытом слое, 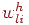- величина связи, между 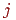-м входным и 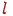-м скрытым нейронами 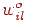- вес связи между 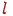-м скрытым и 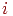-м выходным нейронами.

Использование регуляризирующего члена 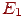приводит к дифференциации весов по величи-нам, уменьшая большинство, но сохраняя значения некоторых из них. Обучение сети произво-дится методом обратного распространения ошибки.