Метод Кинцеля. Уничтожение фрустрированных связей.

“Ложная память” имеет интересный нетривиальный смысл и в случае использования других правил обучения, минимизирующих энергию нейронных сетей.

Одно из них было предложено в 1985 году Кинцелем, который основывал свои рассуждения на реальном наблюдении, согласно которому у ребенка в первые несколько лет жизни отмирает большое число синапсов, хотя именно в это время он учится и усваивает огромное количество информации (Kinzel, 1985). Подобное явление подсказало Кинцелю следующий метод обучения. Возьмем полностью неорганизованную сеть нейронов с нулевыми порогами и связями, величины которых имеют Гауссово распределение с нулевым средним, и ликвидируем в ней все фрустрированные в векторах памяти соединения. То есть для всех запоминаемых векторов обнуляются все связи, для которых . В результате получается сеть, в которой все состояния кодируемые векторами , очевидно, будут стационарными.

Требование нефрустрированности каждой связи для всех запоминаемых векторов, конечно, очень сильное. Для слабо коррелированных образов приходится уничтожать так много межнейронных соединений, что в полученной слабосвязанной сети почти все состояния оказываются стабильными, т.е. появляется большое число “ложных” образов. (Если нейроны вообще не связаны - , то все возможные состояния сети стационарны). Положение улучшается, если запоминаемые векторы коррелированы друг с другом. Количество стационарных состояний при этом уменьшается, что было продемонстрировано Кинцелем в ходе компьютерного моделирования. Тем не менее, полное число стационарных состояний не может быть уменьшено до набора запоминаемых векторов. Минимальная память в этой сети представляет собой все возможные комбинации векторов минимального базиса, за исключением тех из них, в которых коррелируют состояния нейронов, антикоррелирующие в запоминаемых векторах. Сеть с такой минимальной памятью может быть получена с помощью простой модификации метода уничтожения фрустрированных связей, который стартует с сети, у которой величины всех синаптических связей положительны и равны между собой, и не уничтожает, а инвертирует знак связи, фрустрированной во всех запоминаемых состояний. В примере, иллюстрируемом приводимым ниже рисунком,

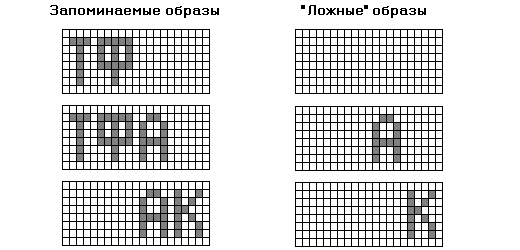
Рисунок 28. Слева - состояния, запоминаемые в сети Кинцеля . Справа - “ложные” образы.

в сети из 168 нейронов, организованных в двумерную структуру, запоминаются три образа: (ТФ__) (ТФА_)и(__АК). “Ложными” образами для сети с минимальной памятью будут при этом: пустое поле (____); (__А_); (___К) и их негативы. Невозможно раздельное появление в образе памяти (Т___) и (_Ф__), так как им соответствует один вектор минимального базиса. Невозможно также появление стационарного состояния (ТФ_К), так как в заучиваемых образах присутствие (ТФ__) исключает присутствие (___К) и наоборот.

Неустранимость ложной памяти. Запрещенные наборы,

Мы рассмотрели Хеббовское и Кинцелевское правила построения синаптических связей и убедились, что соответствующие сети демонстрируют нетривиальное отображение множества заучиваемых образов на множество аттракторов сети. В частности, ряд аттракторов далеки от заучиваемых образов и квалифицируются как ложная память. Возникает естественный вопрос о существовании такого метода обучения, который вообще бы устранял дополнительную память.

Оказывается, что ответ на него в общем случае отрицательный. Имеются такие наборы образов, что какую бы матрицу синаптических связей и пороги нейронов, гарантирующие их стационарность, мы не выбрали, в сети с неизбежностью возникнут иные аттракторы.

В частности, уже в сети из трех нейронов невозможно обеспечить стационарность только следующих четырех состояний: (0,0,0), (1,1,0), (1,0,1) и (0,1,1) или симметричного набора состояний. Такие наборы векторов, которые не могут составлять и исчерпывать память сети, называют запрещенными. Можно показать, что для сети из трех нейронов два приведенных выше множества векторов исчерпывают все запрещенные наборы образов.

В сети из четырех нейронов не реализуемы уже 40 наборов векторов, но все они могут быть получены всего из двух независимых наборов преобразованием однотипности - перестановками переменных и инверсией. Такая тенденция является обнадеживающей с точки зрения возможностей сетей к запоминанию образов, поскольку доля не реализуемых функций падает. Однако сети, аттракторы которых сконструированы заранее, могут имитировать только ассоциативную память, не создающую новой информации. Нас же сейчас интересует как раз эффект обобщения, присущий рекуррентным сетям, так же как и обычным персептронам.

Версии протитипа

Итак, структура аттракторов в модели Хопфилда может допускать различные содержательные интерпретации. В том случае, когда она совпадает со структурой запоминаемых образов, мы говорим об ассоциативной памяти (пассивной). Если, напротив, в сети формируется единственный аттрактор, в каком-то смысле являющийся прототипом этих образов, то проявляется способность сети к обобщению (generalization). В общем же случае структура аттракторов сети настолько сложна, что на первый взгляд не допускает какой-либо наглядной трактовки. Действительно, такая трактовка должна быть настолько универсальной, чтобы включать режимы запоминания и обобщения в качестве предельных случаев. Тем не менее, она возможна и опирается на рассуждения, которые приводятся в данном разделе.

Начнем с рассмотрения сети Хопфилда, в память которой, согласно правилу Хебба, записан только один образ . В этом случае синаптические связи определяются выражением

У такой сети есть только два зеркально симметричных стационарных состояния . Если она перейдет в одно из них, то величина энергии в минимуме составит

Заметим, что все связи в сети дают в энергию одинаковый отрицательный вклад и поэтому являются не фрустрированными. Напомним, что условием фрустрации связи в состоянии сети является неравенство .

Именно это условие не выполняется ни для одной связи в сети с записанным единственным образом. Мы можем трактовать подобную ситуацию так, что сеть с одним записанным в нее образом точно воспроизводит его в виде своего аттрактора (с точностью до зеркального отражения), и если мы выберем в этой сети случайную связь, то вероятность ее фрустрации будет равна нулю.

Таким образом, сеть Хопфилда идеально приспособлена для хранения единственного образа.

Рассмотрим теперь следующую систему (см. Рисунок 29). Пусть в Хопфилдовской сети-передатчике (слева) записан единственный образ , который нам неизвестен. Этот образ многократно передается в Хопфилдовскую сеть-приемник (справа) в виде сообщения через канал с шумом. При его прохождении образ искажается так, что некоторые компоненты кодирующего его вектора меняют свой знак на противоположный.

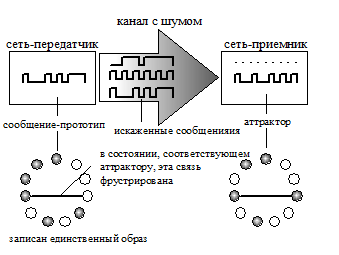
Рисунок 29. Вверху: интерпретация стационарных состояний в сети Хопфилда как локально наиболее правдоподобных версий сообщения, многократно переданного сетью-передатчиком в сеть-приемник через канал с шумом. Внизу: сети с записанным единственным сообщением прототипом (слева) и со всеми искаженными версиями этого сообщения (справа).

Задача сети-премника состоит в том, чтобы имея P полученных сообщений восстановить исходное сообщение . Исходя из полученных сообщений, оценим вероятность того, что в исходном сообщении компоненты и имеют одинаковое или противоположные значения. Для этого нужно просто подсчитать, в скольких из P сообщений произведения положительны или отрицательны и отнести это число к полному числу сообщений. Формально эти вероятности можно записать как

.

Вспоминая выражение для правила Хебба, убеждаемся что если сообщения , полученные сетью-приемником, сформируют свои связи в соответствие с ним, то тогда

.

Используя последнее соотношение, преобразуем выражение для энергии состояния в сети-приемнике к виду

.

Поскольку мы не знаем точного вида сообщения , записанного в связях сети-передатчика, то мы не знаем и величин этих связей. Однако, мы можем задаться следующим вопросом: если состояние сети-передатчика совпадает с состоянием сети-приемника , то какова вероятность, что случайно выбранная связь в сети-передатчике окажется фрустрированной. Легко увидеть, что эта вероятность равна

.

Таким образом, энергия состояния сети-приемника с точностью до постоянных множителя и слагаемого совпадает с вероятностью фрустрации случайно выбранной связи в сети-передатчике, оцененной по полученным от нее сообщениям.

Однако в сети-передатчике записано лишь одно сообщение, и вероятность фрустрации связей в ней равна нулю. Но поскольку ни сообщение, ни соответствующие ему связи сети-передатчика нам не известны, мы можем лишь пытаться найти такое состояние сети-приемника, которое хотя бы локально минимизирует эту вероятность. Подобные состояния были бы локально наилучшими версиями сообщения, посылаемого сетью-передатчиком. А так как вероятность нахождения фрустрированной связи в передатчике связана с энергией состояния в приемнике, то такими наилучшими версиями как раз и окажутся состояния, соответствующие энергетическим минимумам сети-приемника. Таким образом, все аттракторы сети Хопфилда, связи которой сформированы согласно правилу Хебба, исходя из набора обучающих векторов , могут трактоваться как наиболее вероятные версии некоторого сообщения, переданного P раз через канал с шумом и представленных заучиваемыми векторами.

Подобный подход устраняет деление состояний памяти на истинные и ложные, давая им единую интерпретацию. В такой трактовке функционирование сети Хопфилда в качестве пассивной памяти соответствует случаю, когда шум в канале очень велик, т.е. все принимаемые сетью сообщения некоррелированы. Это не дает ей возможности выделить из них сообщения и, рассматривая их как равноправные его версии, сеть генерирует аттрактор в каждой точке N-мерного пространства . Если же, напротив, шум в канале невелик, т.е. все запоминаемые векторы мало отличаются от передаваемого сообщения, в сети вырабатывается его единственная версия.

Хотя первоначально сеть Хопфилда привлекалась для объяснения свойств ассоциативной памяти, можно привести множество различных примеров ее применения и для выделения зашумленного сигнала-прототипа. В качестве одного из таких примеров мы рассмотрим один - поиск промоторов в ДНК