Энергия состояния

Нетрудно показать, что описанная выше асинхронная динамика сети сопровождается уменьшением энергии сети, которая определяется следующим образом:

.

Действительно, при изменении состояния одного -го нейрона его вклад в энергию изменяется с на . Следовательно,

.

В случае, когда нейрон имеют ненулевые пороги активации, энергия состояния приобретает вид + , но вышеприведенный вывод остается в силе.

Поскольку число нейронов в сети конечно, функционал энергии ограничен снизу. Это означает, что эволюция состояния сети должна закончиться в стационарном состоянии, которому будет соответствовать локальный минимум энергии. В Хопфилдовской модели стационарные конфигурации активностей нейронов являются единственным типом аттракторов в пространстве состояний сети. Мы можем представить динамику сети, сопоставив ее состояние с шариком, движущимся с большим трением в сложном рельефе с множеством локальных минимумов. Сами эти минимумы будут устойчивыми состояниями памяти, а окружающие точки на склонах - переходными состояниями.

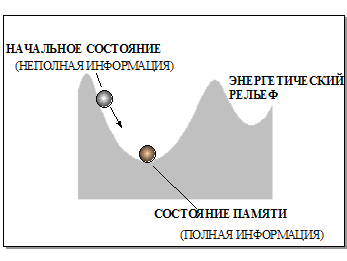
Рисунок 27. Поведение состояния в сети Хопфилда аналогично движению шарика, скатывающегося со склона в ближайшую лунку. Начальное состояние шарика соответствует вектору, содержащему неполную информацию об образе памяти, которому отвечает дно лунки.

Такая динамика определяет главное свойство сети Хопфилда - способность восстанавливать возмущенное состояние равновесия - "вспоминать" искаженные или потерянные биты информации. Восстановление полной информации по какой-либо ее части - вспоминание по ассоциации - наделяет модель Хопфилда свойством ассоциативной памяти. (Далее в этой главе мы продемонстрируем, и более общие возможности сети Хопфилда.)