Гибридное обучение
Относительная автономность базисных функций позволяет разделить обучение на два этапа. На первом этапе обучается первый - соревновательный - слой сети, осуществляя квантование данных. На втором этапе происходит быстрое обучение второго слоя матричными методами, т.к. нахождение коэффициентов второго слоя представляет собой линейную задачу.
Подобная возможность раздельного обучения слоев является основным достоинством сетей радиального базиса. В целом же, области применимости персептронов и сетей радиального базиса коррелируют с найденными выше областями эффективности квантования и понижения размерности (см. Рисунок 19).
Выводы
В этой главе мы познакомились со вторым из двух главных типов обучения - обучением без учителя. Этот режим обучения чрезвычайно полезен для предобработки больших массивов информации, когда получить экспертные оценки для обучения с учителем не представляется возможным. Самообучающиеся сети способны выделять оптимальные признаки, формируя относительно малоразмерное пространство признаков, без чего иногда невозможно качественное распознавание образов. Таким образом, оба типа обучения удачно дополняют друг друга. Кроме того, как мы убедились на примере сетей с узким горлом, между этими типами обучения существует тесная взаимосвязь: если посмотреть на ситуацию под определенным углом зрения, соответствующие правила обучения подчас просто совпадают.
Bell, A.J., Sejnowsky, T.J. (1995). "An information-maximization approach to Blind Separation and Blind Deconvolution". Neural Computation7, 1129-1159.
Bishop, C.M. Neural Networks and Pattern Recognition. Oxford Press. 1995.
Deboeck, G. and Kohonen, T. (Eds). Visual Explorations in Finance with Self-Organizing Maps. Springer, 1998.
Hebb, D.O. (1949). The Organization of Behavior. New York: Wiley.
Hertz, J., Krogh, A., and Palmer, R. Introduction to the Theory of Neural Computation. Addison-Wesley, 1991.
Kohonen, T. (1982). "Self-organized formation of topologically correct feature maps". Biol. Cybernetics 43, 56-69.
Kohonen, T. Self-Organizing Maps. Springer, 1997 (2-nd edition).
Linsker, R. (1992). Local synaptic learning rules suffice to maximize mutual information in linear network". Neural Computation4, 691-702.
Oja, E (1982). "A simplified neuron model as a Principal Component Analyzer", J. Math. Biology, 16, 267-273.
Oja, E., Ogawa, H., and Wangviwattana J., (1991) "Learning in nonlinear constrained Hebbian networks", in Artificial Neural Networks (Proc. ICANN-91), T.Kohonen et al. (Eds.). Amsterdam: North-Holland, 385-390.
Рекуррентные сети: Ассоциативная память
Сеть Хопфилда и спиновые стекла. Энергия и динамика сети. Ассоциативная память: запись и воспроизведение. Емкость памяти: термодинамический подход. Чувствительность к огрублениям и повреждениям связей. Повышение емкости памяти: разобучение. Запоминание последовательностей образов. Сеть Хопфилда с точки зрения теории информации. Выделение прототипов и предсказание новых классов.
& Самое худшее случилось - сказал сэр Дональд Акер, когда в Массачусетском Технологическом Институте соединили входы с выходами С.Лем, Не буду прислуживать
Мы уже познакомились с сетями, обучаемыми с учителем, задающим образцы правильных ответов, и обучаемыми без учителя, которые адаптируют свою структуру к данным не требуя дополнительной информации о принадлежности их к тому или иному классу. Однако до сих пор мы ограничивались сетями без обратных связей. Такие сети, будучи обучены, выдают ответ сразу после прохождения через них входного сигнала. Каждый нейрон, при этом срабатывает лишь однажды. Соответственно, достаточно глубокая, многостадийная обработка данных подразумевает наличие многих слоев, что усложняет обучение. Естественным обобщением таких однопроходных схем служат т.н. рекуррентные сети, выходы которых возвращаются обратно на их входы. Тем самым, информация пропускается через одну и ту же сеть многократно.
Новое качество, присущее рекуррентным сетям, - динамическая обработка информации.
Одной из наиболее известных моделей такого рода, которая оказала важнейшее воздействие на возрождение интереса к нейронным сетям в восьмидесятые годы, является сеть Хопфилда. В данной главе мы рассмотрим структуру и свойства этой сети, делающие ее таким привлекательным объектом как теоретических, так и прикладных исследований.
Исторический поворот в 1982 году
В 1982 году в докладах Американской академии наук была опубликована статья американского физика, специалиста в области физики твердого тела из Калифорнийского Технологического Института, Джона Хопфилда (Hopfield, 1982a). С этой работы начался бурный процесс возрождения интереса к искусственным нейронным сетям, на который так негативно повлияла в конце шестидесятых книга Минского и Пейперта. В работе Хопфилда впервые было обращено внимание на аналогию, которая существует между сетями с симметричными связями и давно известными физикам объектами - спиновыми стеклами. Кроме того, стало ясно, что такие сети служат прекрасной основой для построения моделей содержательно-адресованной памяти. И, наконец, обнаружилось, что нейронные сети могут быть успешно исследованы с помощью методов теоретической физики, в частности, статистической механики. Результатом этого обстоятельства явилось массовое внедрение физиков и физических методов в эту новую область знания.
Спиновые стекла
В кристаллической решетке атомы, обладающие магнитными моментами, могут взаимодействовать друг с другом различными способами. Если связи между моментами таковы, что стремятся сориентировать их параллельно, то в основном состоянии (состоянии минимальной энергии) все атомы в решетке ориентируют свои моменты параллельно. Такие вещества называются ферромагнетиками. Связи между атомами описываются при этом одинаковыми положительными числами и называются также ферромагнитными. Если, напротив, все связи отрицательны, то такие вещества называются антиферромагетиками. В антиферромагнетиках соседние спины ориентируются в противоположных направлениях. А вот если связи между магнитными моментами атомов имеют случайные значения знаков, то соответствующие системы называются спиновыми стеклами (см. Рисунок 24). Основная особенность системы связей в спиновых стеклах такова, что система в целом оказывается фрустрированной.
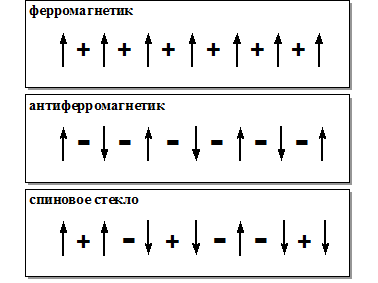
Рисунок 24. Знаки связей между спинами в ферромагнетике, антиферромагнетике и спиновом стекле
Фрустрация (“разочарование”) означает, что как бы ни сориентировались отдельные магнитные моменты атомов в спиновом стекле, всегда найдутся такие пары из них, в которых взаимодействие вносит положительный (разочаровывающий) вклад в энергию состояния (см. Рисунок 25).
Фрустрированность системы обусловливает огромное вырождение ее основного состояния. Спиновое стекло может “замерзнуть” в любом из возможных основных состояний системы, отличающемся от множества других аналогичных состояний с практически такой же энергией лишь конфигурацией системы магнитных моментов. Хопфилд предположил, что аналогичное явление может лежать в основе существования огромного числа состояний памяти, характерного для мозга. Действительно, можно рассмотреть модель полносвязной нейронной сети с рекуррентными симметричными связями между нейронами. В такой модели возбуждающим связям будут соответствовать ферромагнитные связи в спиновом стекле, а тормозным - антиферромагнитные связи.
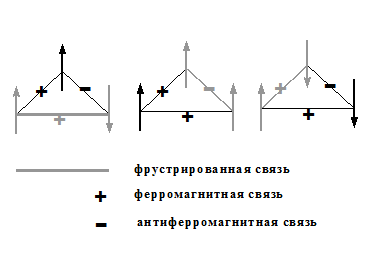
Рисунок 25. Фрустрированная система трех взаимодействующих спинов. При любых их ориентациях всегда находится такая связь , знак которой противоречит взаимной ориентации пары, что приводит к нежелательному положительному вкладу в полную энергию системы.
Подобно спиновым стеклам, такие сети будут иметь множество стационарных конфигураций активностей нейронов, являющихся аттракторами (от англ. attract - притягивать), т.е. такими состояниями, к которым сходится динамика нейросети. Именно введенная Хопфилдом динамика изменений состояний нейронов наряду с симметричностью связей между нейронами определили новизну описываемой модели.
Дата добавления: 2015-04-10; просмотров: 1779;
