Метод Флёри построения эйлерова цикла

Метод Флёри построения эйлерова цикла начинает работу с некоторой вершины х и каждый раз вычеркивает пройденное ребро. Не проходить по ребру, если удаление этого ребра приводит к разбиению графа на две связные компоненты (не считая изолированных вершин).

Опишем алгоритм построенияэйлерова цикла в связном неорграфе с четными степенями вершин, а также в орграфе с совпадающими полустепенями захода и исхода.

Замечание. Граф G=(X,V) задается множеством X своих вершин и набором реберных окрестностей всех его вершин S(x)={v |ребро v инцидентно вершине х}.

Шаг 1. Выбрать произвольную вершину х₀ÎX и положить х=x₀, z=х₀, С=x₀, D=x₀, где С - чередующаяся последовательность вершин и ребер, представляющая строящийся эйлеров цикл; D - чередующаяся последовательность, представляющая начальный отрезок цикла, который будет присоединен к текущему циклу С; х - конечная вершина в последовательности D; z - вершина на цикле С, которая служит началом D.

Шаг 2. В множестве S(x)\[V(С)ÈV(D)] выбрать произвольное ребро 1. Если S(x)=Æ, то прейти к шагу 5. Здесь V(С) и V(D) обозначают множество ребер из С и D.

Шаг 3. К D дописать ребро 1 и его конец у, т.е. положить D ={ D, 1, у}.

Шаг 4. Положить х=у и перейти к шагу 2.

Шаг 5. Присоединить к С в вершине z цикл D, т.е. положить C={C[x₀,z),D,C(z,x₀]}, где C[x₀,z) - начальный отрезок последовательности С до веpшины z, не включая z; C(z,x₀] – отрезок последовательности С от z до x₀, не включая z.

Шаг 6. Просматривая последовательность С слева направо, ищем первую такую вершину v, что S(v)\V(C)=Æ. Если такой вершины нет, то перейти к шагу 8, иначе перейти к шагу 7.

Шаг 7. Положить x=v, z=v, D=v и перейти к шагу 2.

Шаг 8. ВыдатьпоследовательностьС, которая является эйлеровым циклом.

4.12.2. Метод перебора Робертса и Флореса для построения гамильтоновых путей и контуров

Метод состоит в выполнении следующей последовательности шагов.

Шаг 1. Построить матрицу 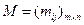, n=|X|, m=max{d(x_i)}, m_ij , x_iÎX . m_ij - есть j-я вершина (скажем, x_k), для которой в графе G=(X,Г) существует дуга (x_i,x_k) (вершины в столбцах упорядочены).

Шаг 2. Положить p=x₁ (x₁ – отправная вершина), S={x₁}.

Шаг 3. Если в столбце р существует возможная вершина (под возможной понимается вершина, еще не принадлежавшая S), то перейти к шагу 4, иначе к шагу 7.

Шаг 4. Выбрать первую возможную вершину x_k. Положить S=SÈ{x_k}, p=x_k и перейти к шагу 5.

Шаг 5. Если |S|=n-1, то напечатать гамильтонов путь S и перейти к шагу 6, иначе перейти к шагу 3.

Шаг 6. Если существует дуга (p,x₁), то напечатать гамильтонов контур (SÈ{x₁}), иначе перейти к шагу 7.

Шаг 7. Удалить последнюю включенную в S вершину x₁. Если S=Æ, то процесс заканчивается, так как все пути и контуры найдены. Останов. Иначе положить p=x_i-1 и перейти к шагу 3.

Пример. Рассмотрим граф, изображенный на рис. 4.43.