Пример. Математическая постановка задачи нахождения оптимальной последовательности выпуска изделий.

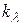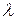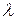Введем некоторые обозначения. Пусть {a₁…a_L} - множество всевозможных последовательностей выпуска изделия L модификаций; - количество оборудования в группе , где =1,…,N; 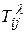- время, необходимое на переналадку единицы оборудования 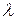-ой группы при переходе с выпуска i-ой модификации на выпуск j-ой модификации.

Пусть G - ориентированный граф, вершины которого представляют изделия, а существование дуги (х_i, х_i) означает, что изделие j может следовать за изделием i без перенастройки оборудования. Тогда, если в этом графе есть гамильтонов цикл (ориентированный цикл, проходящий через каждую вершину графа), то существует последовательность выпуска изделий, не требующая перенастройки оборудования. Если не существует циклической последовательности выпуска изделий, не требующей перенастройки оборудования, то задача сводится к нахождению последовательности выпуска изделий, требующих наименьших затрат на перенастройку оборудования.

Пусть х_ij =1, если после изделия i-ой модификации выпускается изделие j-ой модификации; х_ij=0, если после изделия i-ой модификации изделие j-ой модификации не выпускается.

С так введенными переменными ставим задачу:

Минимизировать функцию

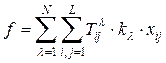(1)

при условиях

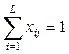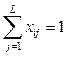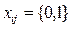, , . (2)

В качестве дополнительных ограничений необходимо наложить условие «петель», для устранения подконтуров в задаче

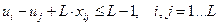(3)

Задача (1)-(3) полностью аналогична классической задаче коммивояжера:

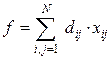(4)

при условиях

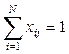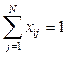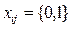, , . (5)

условие «петель»

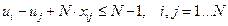(6)

В задаче коммивояжера (4)-(6) ищется оптимальная последовательность обхода «городов», а в задаче (1)-(3) оптимальная последовательность выпуска изделий. В задаче (4)-(6) матрица D с элементами 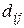является матрица расстояний между N «городами», этой матрице соответствует матрица В в задаче (1)-(3) с элементами 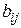, которая является матрицей времени переналадки оборудования

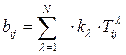
Таким образом, задачу оптимизации последовательности выпуска изделий можно решить методами решения задачи коммивояжера.

Плоские и планарные графы

Во многих случаях не имеет значения, как изобразить граф, поскольку изоморфные графы несут одну и ту же информацию. Однако встречаются ситуации, когда важно выяснить, возможно ли нарисовать граф на плоскости так, чтобы его изображение удовлетворяло определенным требованиям.

Плоским графом называется граф, вершины которого являются точками плоскости, а ребра – непрерывными линиями без самопересечений, соединяющими соответствующие вершины так, что никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины.

А б

Рис. 4.45. Плоские графы

Любой граф, изоморфный плоскому графу, будем называть планарным. Граф на рис. 4.46 является планарным, так как он изоморфен графу на рис. 4.45.б.

Рис.4.46

Очевидны следующие утверждения:

1) всякий подграф планарного графа планарен;

2) граф планарен тогда и только тогда, когда каждая его связная компонента – планарный граф.

О планарных графах говорят, что они укладываются на плоскости (имеют плоскую укладку).