Модульные свойства паттерновых сетей

Сегодня информационные и иные модульные системы, обычно, представляются графами и их разновидностями, например, сетями Петри. Однако графы мало пригодны для моделирования модульных систем по двум причинам. Они не моделируют внутренние границы модульных систем, поскольку ребра графов нельзя разъединять и затем вновь соединять. Кроме того графы не четко изображают входы и выходы (внешние границы) модульных систем. В отличие от графов, паттерновые сети разъемны и обладают ярко выраженными модульными свойствами, так как они состоят из образующих, представляющих собой логические модульные элементы. Превосходство паттерновых сетей в изображении внутренних и внешних границ открытых модульных систем, по сравнению с графами, иллюстрирует Рис.7.1.

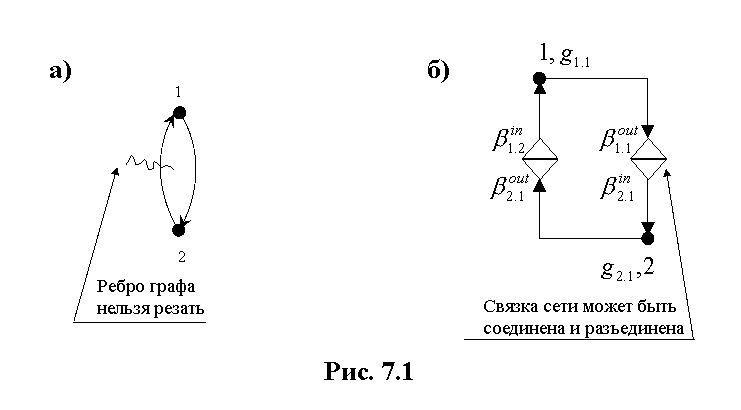
На Рис.7.1а изображен элементарный ориентированный граф. На нем показано, что ребро графа нельзя разрезать (разъединить). Ниже на Рис.7.1б изображена наглядная схема линейной ориентированной паттерновой сети, состоящей из двух линейных ориентированных образующих g1, g2. Образующая g1 имеет вершину и две связи (bonds). Вершина изображена точкой и помечена именем (идентификатором) образующей, роль которого выполняет символ g, помеченный индексом 1. Помимо вершины образующая g1 имеет две ориентированный связи - входную и выходную. Входная связь представлена треугольником и стрелкой, направленной к точке, а выходная связь стрелкой направленной от точки и треугольником. Образующая g2 имеет аналогичную наглядную схему. На рисунке выходная связь первой образующей соединена с входной связью второй образующей, в результате чего из двух соединенных треугольников образовался ромб. Ромб и две примыкающие к нему стрелки называются связкой образующих g1 и g2 или связкой паттерновой сети. Каждой связи на Рис.7.1б приписаны переменные, обозначенные символами с соответствующими нижними числовыми индексами и верхними индексами in и out. Индексы in и out означают, что переменные присвоены соответственно входным и выходным связям образующих. Четырем переменным поставлены в соответствие четыре области значений (данных), обозначенные символами D, и называемые доменами. В доменах содержатся значения, которые могут присваиваться переменным . Если двум переменным , участвующим в связке присвоены значения, удовлетворяющие условию соединения связки, то связка является истинной (замкнутой). Если переменным присвоены значения, не удовлетворяющие условию соединения связки, то связка является ложной (разомкнутой). Образующие g1 и g2 служат обобщенными моделями двух реальных модулей, каждый их которых имеет один вход и один выход. Паттерновая сеть, показанная на Рис.7.1б, моделирует два реальных модуля выход одного из которых соединен с входом другого. Несоединенные связи этой паттерновой сети изображают открытые для соединения вход и выход реальной системы, состоящей из двух соединенных модулей.

Таким образом Рис.7.1 показывает, что паттерновая сеть - это разъемная конфигурация, а граф является неразъемной структурой. В дискретной теории паттернов можно создавать образующие с различными числами входных и выходных связей и затем соединять множество таких образующих в паттерновые сети, моделирующие сложные открытые модульные системы. При этом на связках паттерновых сетей, моделирующих реальные модульные системы, можно устанавливать разные условия соединения связок. Например, одни условия соединения устанавливаются на связках паттерновых сетей, моделирующих компьютерные гипертексты, другие условия соединения – на связках паттерновых сетей, моделирующих нейросети мозга. Одно из достоинств паттерновых сетей заключается в возможности изучения и сопоставления с их помощью многообразных условий соединений выходов и входов различных реальных модулей, из которых состоят конкретные физические и логические модульные системы, существующие в природе и обществе.

На Рис.7.1 показана очень простая паттерновая сеть, состоящая всего лишь из двух образующих, причем каждая из них имеет только две связи - входную и выходную. Такая сеть может моделировать, например, две строки, видимые на экране дисплея. Далее вы увидите, что образующие могут иметь много входных и выходных связей, а паттерновые сети могут состоять из многих соединенных между собой образующих. Такими паттерновыми сетями, более сложными чем сеть Рис.7.1б, можно моделировать гипертексты, веб-курсы и иные модульные системы.

Наглядная схема простой линейной ориентированной паттерновой сети (Рис.7.1) и приведенное здесь ее словесное пояснение помогут вам понять формальные описания и наглядные схемы сложных образующих и паттерновых сетей, рассмотренных в последующих лекциях.