Параметрический вектор компонент образующих

Практика решения инженерных задач показала, что логические и физические модули с входами и выходами эффективно моделируются ориентированными образующими, определяемыми следующим параметрическим вектором компонент:

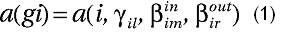
Компоненты 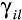, , 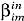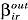параметрической образующей gi делятся на две группы. Компоненты первой группы, представленные символами с нижними индексами, называются атрибутами образующей. Если l=1, то образующая gi имеет только один атрибут 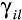. Компоненты второй группы, представленные в векторе (1) символами 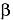, называются в общей теории паттернов показателями связей образующей. В дискретной теории паттернов показатели связей 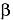и атрибуты 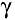вектора (1) трактуются как переменные, имеющие соответствующие области значений.

Параметры l,m,r, фигурирующие в нижних индексах переменных и образующей gi, могут принимать различные числовые значения:

l=1,2,...; m=0,1,2,...; r=0,1,2,.... В результате изменения значений параметров m,r из вектора (1) получаются векторы компонент образующих с разными числами входных и выходных связей.

Образующие, определяемые параметрическим вектором (1), представляют в обобщенной форме лишь структуры реальных модулей. Чтобы образующие моделировали не только структуры, но и информационное содержание модулей, в дискретной теории паттернов переменным 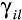, , 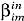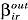вектора (1) ставятся в соответствие множества:

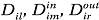(2), называемые доменами.

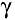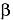В доменах помещаются данные присваиваемые переменным и векторов компонент образующих.

Для получения образующих с разными числами входных и выходных связей параметры m,r в векторе (1) заменяются конкретными числами. Одновременно эти параметры заменяются в доменах (2) такими же числами.

Очевидно, что параметрический вектор (1) и его домены (2) представляют собой параметрические образы структур и содержаний многих образующих, имеющих различные числа входных и выходных связей.

Особыми являются случаи, когда параметры m и r принимают в векторе (1) и доменах (2) значения равные нулю. В случае, когда m=0 переменная 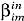и домен 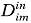исключаются из соотношений (1) и (2). В случае, когда r=0 из соотношений (1), (2) исключаются переменная 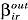и домен 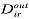. Благодаря этим условиям обнуления параметров m,r обеспечивается моделирование образующих, не имеющих входных и выходных связей.

В дискретной теории паттернов применяются три вида образующих - абстрактные, конкретные и ассоциированные.

Абстрактная образующая определяется следующим образом. Во все домены образующей помещается неопределенное значение данных, обозначаемое символом 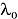. Образующая называется абстрактной, если во всех ее доменах содержится только символ 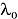и ни в одном из них нет конкретных данных, характеризующих реальные модульные объекты. Следовательно абстрактная образующая не определена на какой-либо конкретной информационной среде. Образно говоря, все абстрактные образующие определены на "пустой" информационной среде, обозначаемой символом .

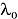Образующая, в доменах которой помимо символа 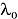помещены данные об одном или нескольких реальных модулях, называется конкретной. Абстрактная образующая превращается в конкретную после размещения в ее доменах данных о реальных модулях. Конкретные образующие занимают промежуточное положение между абстрактными и ассоциированными образующими. Домены конкретных образующих определяются в общем случае как конечные или счетные множества значений переменных 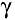и 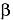. В этом они аналогичны доменам атрибутов реляционных отношений, которые определяются в теории реляционных баз данных как конечные или счетные множества значений атрибутов.

Если переменным 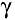и 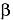конкретной образующей присваиваются взятые из доменов данные о реальном модуле, то образующая становится ассоциированной с данными и служит паттерновой моделью этого модуля.

Кратко, абстрактные, конкретные и ассоциированные образующие можно охарактеризовать следующим образом. Абстрактные образующие имеют абстрактные вектора компонент и "пустые" домены, содержащие символы 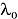. Конкретные образующие имеют абстрактные вектора компонент и домены, содержащие конкретные данные об одном или многих реальных модулях. Ассоциированные образующие имеют вектора компонент, ассоциированные с данными об одном реальном модуле и домены, содержащие конкретные данные об одном или многих реальных модулях.

Абстрактные, конкретные и ассоциированные образующие, не только представляются своими векторами компонент и доменами. Они также изображаются наглядными схемами, рисуемыми на бумаге или экранах дисплеев. Наличие у образующих наряду с формальными представлениями в виде векторов компонент также наглядных схем исключительно важно для практики.