Оценка значимости фактора

Когда основным источником погрешности являются случайные ошибки измерений, то в точках плана обычно проводятся однократные опыты. В такой ситуации ошибки различных опытов считают взаимно независимыми случайными величинами, распределенными по нормальному закону с нулевым математическим ожиданием и одинаковой, хотя и неизвестной, дисперсией. Следовательно, функция отклика в различных точках плана также распределена нормально. Ее математические ожидания неизвестны и могут быть различными. Оценка влияния фактора в этих условиях проводится на основе применения метода дисперсионного анализа, суть которого заключается в определении значимости различий между средними значениями функции отклика для разных значений исследуемого фактора [3, 7]. Такое сравнение производится не путем непосредственного сравнения средних значений, а путем сопоставления факторной дисперсии функции отклика и остаточной дисперсии, вызванной случайными причинами. Если дисперсия функции отклика, порожденная воздействием различных значений фактора, значимо превышает остаточную дисперсию, то фактор оказывает существенное влияние на функцию отклика. А это значит, что и средние значения функции отклика на разных уровнях фактора различаются существенно.

Итак, исходными данными являются:

план на латинском (греко-латинском, гипер-греко-латинском) квадрате с количеством уровней изменения факторов, равном n. Пусть уровни анализируемого фактора Р соответствую столбцам квадрата;

матрица значений функции отклика Y= |y_kj| размерностью n×n;

уровень значимости для проверки статистической гипотезы a.

Дисперсионный анализ включает следующие шаги.

1. Вычисление среднего значения функции отклика по всем опытам и среднего значения по различным уровням фактора Р

.

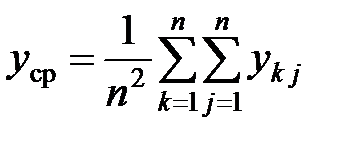
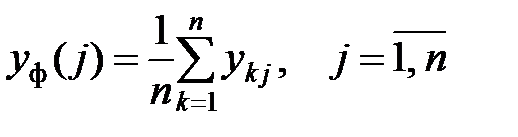2. Оценка факторной дисперсии

.

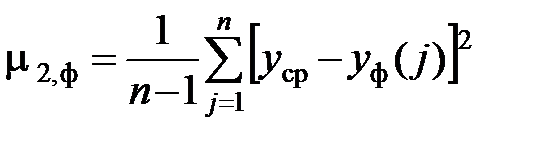3. Оценка остаточной дисперсии

.

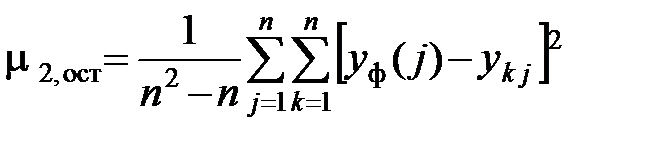4. Оценка значимости фактора Р производится на основе метода проверки статистических гипотез. Нулевая гипотеза Н₀ соответствует равенству средних значений функции отклика при различных значениях фактора. В этом случае факторная и остаточная дисперсия являются несмещенными оценками неизвестной генеральной дисперсии функции отклика и поэтому не должны существенно различаться. Очевидно, если оценка факторной дисперсии не превышает оценку остаточной дисперсии, то справедлива гипотеза Н₀. Альтернативная гипотеза Н₁ соответствует утверждению, что факторная дисперсия существенно больше остаточной дисперсии, следовательно, средние значения также значимо различаются. Проверка осуществляется на основе критерия Фишера F = μ_{2, ф} / μ_{2, ост}. Критическое значение критерия F_кр = F(a; n – 1; n² – n) находят стандартным образом, здесь n – 1 соответствует количеству степеней свободы факторной дисперсии, а n² – n – количеству степеней свободы остаточной дисперсии. Если выполняется условие F > F_кр, то фактор Р существенно влияет на функцию отклика, иначе – влияние фактора не существенно.

Критерий Фишера применим только при сравнении дисперсий нормально распределенных величин. Если такой уверенности нет, то к полученному выводу следует относиться осторожно.

В случае проведения повторных опытов в точках плана распределение средних значений функции отклика будет приближаться к нормальному с увеличением количеств опытов. И применение критерия Фишера будет достаточно обосновано.