Проверка однородности дисперсии воспроизводимости

Необходимым условием применения метода наименьших квадратов для расчета оценок коэффициентов модели является однородность оценок дисперсии воспроизводимости среднего значения функции отклика во всех точках плана. Поэтому обязательным этапом обработки должна быть проверка статистической гипотезы об однородности совокупности дисперсий воспроизводимости. В условиях различного количества опытов в точках плана применяют критерии Фишера или Бартлетта [8, стр. 12].

Если количество повторных опытов в каждой точке плана достаточно велико (больше 7), то средние значения функции отклика можно считать распределенными по нормальному закону. Проверка однородности по критерию Фишера сводится к проверке гипотезы о равенстве дисперсий двух нормально распределенных случайных величин:

из совокупности оценок дисперсии среднего значения функции отклика выбирается минимальное D_{u min} и максимальное D_{u max} значения с числом степеней свободы соответственно j_{u min} и j_{u max};

вычисляется значение критерия Фишера F = D_{u max} / D_{u min}, которое сравнивается с критическим значением F_кр = F(a; j_{u max}; j_{u min}), где a – уровень значимости (обычно a выбирают в пределах от 0,01 до 0,1). Критическая область является односторонней (альтернативная гипотеза допускает между проверяемыми оценками дисперсии соотношение D_{u max} > D_{u min}). Критическое значение определяют по специальным таблицам (например, табл. П.1 приложения) или с использование стандартных функций математических пакетов;

гипотеза об однородности оценок дисперсии воспроизводимости в различных точках плана принимается, если условие F £ F_кр выполняется, и отвергается в противном случае.

Существенным недостатком критерия Фишера является игнорирование всех оценок дисперсии воспроизводимости, кроме максимального и минимального значения.

Проверка однородности по Бартлетту учитывает оценки дисперсии воспроизводимости во всех точках плана и производится на основе вычисления критерия

.

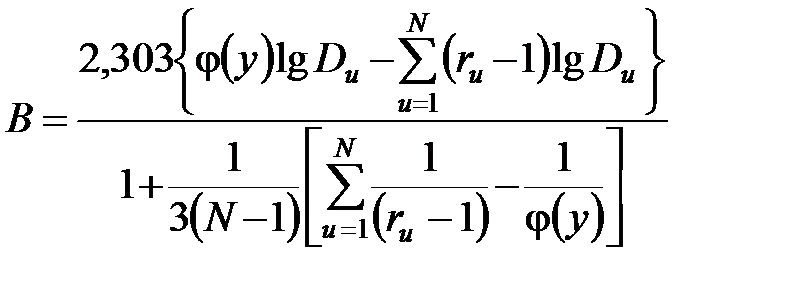Случайная величина В при справедливости гипотезы об однородности дисперсий распределена приближенно как хи-квадрат с N – 1 степенями свободы, если все r_u >3. Следовательно, критическое значение В_кр = c² (a; N – 1), оно определяется по специальным таблицам (например, табл. П.2 приложения) или с использование стандартных функций математических пакетов. Если В £ В_кр, то гипотеза об однородности принимается, при В > В_кр – отвергается.

Критерий Бартлетта чувствителен к отклонениям распределения от нормального, поэтому к результатам сравнения следует относиться осторожно, а при одинаковом объеме опытов в различных точках плана лучше применять критерий Кочрена [8, стр. 13].

Итак, если не выявлена неоднородность дисперсии воспроизводимости, то обработку результатов экспериментов можно продолжать дальше. В противном случае следует выявить и устранить причины неоднородности. Обычно неоднородность является следствием принятых решений по организации и проведению экспериментов.

Во-первых, возможно в экспериментальном исследовании не учтен некоторый существенный фактор (факторы), который изменялся в ходе опытов. Такой фактор (факторы) следует выявить, включить в модель или обеспечить его стабильность в ходе исследований и повторить опыты;

Во-вторых, количество повторных опытов в точках плана с большой дисперсией функции отклика проведено недостаточно. Действительно, дисперсия функции отклика s_u² может существенно различаться в разных точках плана. Так, дисперсия среднего количества заявок в очереди для одноканальной системы массового обслуживания при пуассоновском входном потоке и экспоненциально распределенном времени обслуживания равна r / (1 – r)², где r – загрузка системы. Иначе говоря, эта дисперсия заведомо неоднородна при изменении загрузки. В частности, изменение загрузки от 0,8 до 0,9 приводит к увеличению дисперсии в 4,5 раза. Поэтому для обеспечения однородности дисперсии воспроизводимости среднего значения в точке плана при r = 0,9 следует провести в 4,5 раза больше повторных опытов по сравнению с точкой плана, в которой r = 0,8.

Итак, неоднородность можно снизить за счет уменьшения интервала варьирования факторов или увеличения количества опытов в соответствующих точках плана. Изменение интервалов варьирования влечет необходимость повторения опытов во всех точках плана. Поэтому из указанных способов снижения неоднородности следует выбрать тот, который требует меньшего количества новых опытов.

После того, как установлена однородность дисперсии воспроизводимости, можно приступать к вычислению оценок коэффициентов функции отклика. Оценки коэффициентов функции отклика вычисляются по формулам (3.1). Результаты вычислений этих оценок всегда отличаются от нуля. Но это не значит, что они являются значимыми, т.е. сами коэффициенты не равны нулю. Проверку значимости оценок обычно осуществляют после проверки адекватности модели.