Оценки коэффициентов функции отклика в дробном факторном эксперименте
Применение дробных реплик ведет к смешиванию оценок параметров модели, а их построение предполагает исключение из рассмотрения некоторых взаимодействий факторов. Оценки смешиваются в связи с тем, что каждый из р столбцов дробного факторного плана совпадает с некоторым произведением основных факторов.
Запись плана в виде 2k– p не дает полной характеристики регулярной дробной реплики, так как основные эффекты можно приравнять к различным эффектам взаимодействия. Правило смешивания, определяющее коррелированные основные эффекты и эффекты взаимодействия, удобно описывать с помощью определяющего контраста реплики. Определяющий контраст полуреплики получается путем умножения генерирующего соотношения на его же левую часть, а так как для любой кодированной переменной xi2 =1, то левая часть формулы определяющего контраста всегда равна единице и обозначается I. В частности, для ДФП типа 23 – 1 и генераторе x3 = x1x2 имеет место определяющий контраст I = x1 x2 x3 (генератор умножается на переменную x3, следовательно, x3 x3 = I = x1 x2 x3).
Чтобы определить, с какими параметрами смешана оценка коэффициента данного фактора, следует умножить обе части определяющего контраста на этот фактор. Учитывая равенство xi2 =1, получим порядок смешивания оценок коэффициентов при использовании конкретного плана. Для плана 23 – 1 и определяющего контраста I = x1 x2 x3 порядок смешивания факторов следующий:
x1 = x12 x2 x3 = x2 x3; x2 = x1 x22 x3 = x1 x3; x3 = x1 x2 x32 = x1 x2 .
Оценки коэффициентов линейной модели для этого плана эксперимента не могут быть получены раздельно и будут смешанными:
b1*= b1 + b23 ; b2*= b2 + b13 ; b3*= b3 + b12 .
Планы типа 2k–р являются ортогональными для моделей с взаимодействиями. Поэтому для вычисления оценок коэффициентов получаются простые формулы, как и для ПФЭ
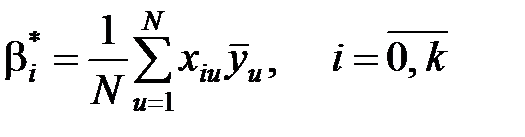 .
.
Планы дробных реплик строят различным образом, но так, чтобы соблюдались основные свойства матрицы планирования. Например, ДФП 23–1можно представить одной из двух полуреплик, генераторами которых являются x3 = x1 x2 и x3 = – x1 x2 соответственно. Определяющие контрасты этих полуреплик: x32 = I = x1 x2 x3 и x32 = I = – x1 x2 x3 .
Смешивание факторов задается соотношениями:
а) первая полуреплика x1 = x2 x3 , x2 = x1 x3 , x3 = x1 x2 ;
б) вторая полуреплика x1 = – x2 x3 , x2 = – x1 x3 , x3 = – x1 x2 .
Коэффициенты линейного полинома полуреплик:
а) β1* = β1 + β23 ; β2* = β2 + β13 ; β3* = β3 + β23 ;
б) β1* = β1 – β23 ; β2* = β2 – β13 ; β3* = β3 – β23 .
Реализовав обе полуреплики, путем сложения и вычитания значений коэффициентов βi* можно получить раздельные оценки для линейных эффектов и эффектов взаимодействия. Такой вариант плана, по сути, соответствует ПФЭ.
Разрешающая способность полуреплик (возможность раздельного определения коэффициентов уравнения) зависит от генерирующих соотношений. Так, если для плана 24 – 1 выбрать генерирующее соотношение x4 = x1 x2, то получим реплику с контрастом I = x1 x2 x4 и разрешающей способностью x1 = x2 x4 и т.д. Здесь линейные эффекты определяются совместно с парными взаимодействиями. Очевидно, что в первую очередь следует пренебречь взаимодействием более высоких порядков из-за их более низкой вероятности существования по сравнению с парными. У полуреплики с контрастом I = x1 x2 х3 x4 или равноценным I = – x1 x2 х3 x4 линейные эффекты будут определяться совместно уже только с тройными взаимодействиями. Это повышает точность оценок параметров модели, так как величина смещения в оценке коэффициента потенциально уменьшается. С ростом количества независимых переменных растет разрешающая способность полуреплик, позволяя оценивать раздельно сначала линейные эффекты, затем парные, тройные взаимодействия и т.д. Но при этом растет и избыточность экспериментов.
Реплики можно строить высокой степени дробности, тем самым сокращая количество экспериментов. Пусть необходимо изучить влияние пяти переменных и известно, что все эффекты взаимодействия пренебрежимо малы. Для линейного приближения следует определить шесть коэффициентов, что потребует применения плана с количеством точек не менее шести. Ближайшее большее число, соответствующее целой степени 2, равно восьми, это дает возможность получить дробную реплику, эквивалентную ПФЭ 23, т. е. реплику 25 – 2 или четвертьреплику. Для построения четвертьреплики необходимы два генерирующих соотношения. В целях построения такой реплики целесообразно пожертвовать тройным и одним из двойных взаимодействий. Пусть этим двойным взаимодействием будет x1x2. Тогда можно построить четыре различные четвертьреплики, каждая из которых задается двумя генерирующими соотношениями:
а) x4 = x1 x2 , x5 = х1 x2 x3 ;
б) x4 = x1 x2 , x5 = – х1 x2 x3 ;
в) x4 = – x1 x2 , x5 = х1 x2 x3 ;
г) x4 = – x1 x2 , x5 = – х1 x2 x3 .
Определяющие контрасты каждой четвертьреплики задаются двумя соотношениями:
а) I = х1 x2 x4 , I = х1 x2 x3 x5 ;
б) I = х1 x2 x4 , I = – х1 x2 x3 x5 ;
в) I = – х1 x2 x4 , I = х1 x2 x3 x5 ;
г) I = – х1 x2 x4 , I = – х1 x2 x3 x5 .
Из этой совокупности четвертьреплик следует выбрать только одну, например, выберем реплику, задаваемую первой парой генерирующих соотношений. Матрица планирования ДФП получается из матрицы ПФЭ 2k–p для k – p основных факторов добавлением р столбцов, элементы которых вычисляются по соответствующим генерирующим соотношениям, табл. 3.3.
Таблица 3.3
| Матрица планирования | Вектор результатов | |||||
| х0 | х1 | х2 | х3 | х4 | х5 | |
| + | – | – | – | + | – | y1 |
| + | + | – | – | – | + | y2 |
| + | – | + | – | – | + | y3 |
| + | + | + | – | + | – | y4 |
| + | – | – | + | + | + | y5 |
| + | + | – | + | – | – | y6 |
| + | – | + | + | – | – | y7 |
| + | + | + | + | + | + | y8 |
Для полной характеристики разрешающей способности четвертьреплик вводят обобщающие определяющие контрасты, третий компонент которых получается путем перемножения попарно первых двух контрастов. Для выбранной четвертьреплики обобщающий определяющий контраст I = х1 x2 x4 = х1 x2 x3 x5 = x3 x4 x5 .
Все совместные оценки находятся путем умножения обобщающего определяющего контраста последовательно на х1, х2 и т.д. В рассматриваемом случае совместные оценки задаются соотношениями:
x1 = x2 x4 = x2 x3 х5 = x1 x3 x4 х5,
x2 = x1 x4 = x1 x3 х5 = x2 x3 x4 х5,
. . . . . . .
x5 = х1 x2 x4 х5= x1 x2 х3 = x3 x4 .
Оценки коэффициентов линейного полинома задаются соотношениями:
β1* = β1 + β24 + β235 + β1345 ,
β2* = β2 + β14 + β135 + β2345 ,
и т. д.
Разрешающая способность выбранной четвертьреплики невысокая – все линейные эффекты определяются совместно с парными взаимодействиями. Этой репликой можно пользоваться для оценки линейных эффектов при условии равенства нулю соответствующих парных взаимодействий. Если такой уверенности нет, то следует применить полуреплику (что требует в два раза большего количества точек плана эксперимента по сравнению с четвертьрепликой) с генерирующим соотношением x5 = х1 x2 x3 x4 , пользуясь которым, можно разделить все линейные эффекты и парные взаимодействия.
Построение обобщающего определяющего контраста для реплик более высокой степени дробности производится аналогично четвертьреплике: исходные контрасты сначала перемножаются попарно, получаются контрасты первого уровня; затем контрасты первого уровня снова перемножаются попарно, получаются контрасты второго уровня и так далее, пока не будет исчерпана возможность перемножения. Если получается два и более одинаковых контрастов, то из них оставляется только один. Обобщающий определяющий контраст составляется путем перечисления выражений для всех сформированных контрастов.
Взаимодействие факторов, выбранных в качестве генераторов плана, может быть значимым или незначимым. Для построения дробных реплик следует выбирать незначимые взаимодействия, которые выбираются по физическим соображениям на основе априорных сведений. Следует учитывать, что ДФЭ позволяет получить несмещенную оценку градиента функции отклика тогда и только тогда, когда ее обобщающий определяющий контраст больше трех. Наличие смещения в оценке градиента увеличивает количество шагов оптимизации, вносит систематическую ошибку в описание функции отклика.
Дата добавления: 2015-03-09; просмотров: 796;
