Проверка адекватности модели

Проверка адекватности математической модели данным эксперимента проводится только в случае ненасыщенного планирования на основе сопоставления дисперсии воспроизводимости среднего значения функции отклика s² (y) и дисперсии адекватности. Оценка дисперсия адекватности характеризует отклонения между результатами наблюдений и значениями, формируемыми по функции отклика

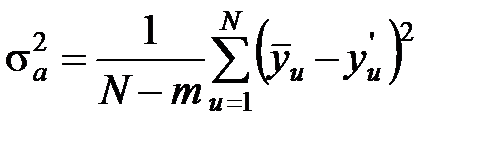, N > m,

где m – количество оцениваемых коэффициентов модели; 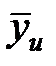– среднее значение результатов наблюдения в u-й точке плана; y^'_u – значение отклика в этой же точке, предсказанное на модели. Количество степеней свободы дисперсии адекватности j_a = N – m. При насыщенном планировании нет степеней свободы и сумма отклонений равна нулю.

Проверка адекватности сводится к проверке гипотезы об однородности оценки дисперсии воспроизводимости s² (y) с количеством степеней свободы j(y) и оценки дисперсии адекватности. Проверка осуществляется по критерию Фишера аналогично рассмотренной выше проверке однородности дисперсий воспроизводимости. Оценки дисперсий в формуле расчета критерия расставляются так, чтобы его величина была больше единицы, критическая область является двусторонней.

Если вычисленное значение критерия меньше критического, то нет оснований для сомнений в адекватности модели. Однако положительный исход статистической проверки не гарантирует достоверной адекватности, а тем более истинности модели, хотя и не противоречит такому предположению. Когда гипотеза отклоняется, следует вывод о неадекватности модели, следовательно, она заведомо не является истинной. Дальнейшее применение неадекватной модели обычно нецелесообразно, и надо принять меры по ее совершенствованию.

Причиной неадекватности могут являться: ошибки в организации и проведении опытов, например неконтролируемое изменение неучтенных в модели факторов; погрешности в задании исходных данных и в измерении результатов; большой размах варьирования факторов и другие причины. Иначе говоря, анализ причин неадекватности требует серьезного изучения сущности исследуемого процесса и методов его исследования.