Моделирование системы дыхания

Моделированию системы дыхания посвящено большое число работ [Петровский Б.В. и др., 1968; Дарбинян Т.М. и др., 1969; Gray, 1945; Horgan, 1968]. Рассмот­рим некоторые из этих моделей, наиболее подходящие для ИВЛ.

Одна из первых моделей дыхания — модель Грея — ис­следует альвеолярную вентиляцию, Ро₂, Рсо₂ и рН крови в ответ на вдыхание углекислого газа. Для выведения закона работы управляющей системы было принято пред­положение, что каждый из трех показателей химического состава крови: Ро₂, Рсо₂ и рН — оказывает независимый и суммарный эффект на альвеолярную вентиляцию и что эти эффекты суммируются. Используя это предположение, был эмпирически выведен закон системы регуляции дыхания в виде приведенной выше статической характери­стики.

Изучение переходных процессов в системе дыхания про­водилось на основе модели Гродинза (1966). В ней ста­тические характеристики управляемой системы полагались нелинейными и описывались системой дифференциальных уравнений второго порядка.

Другой подход к моделированию системы дыхания раз­вивается Д.М. Александером (1968), Б.В. Петровским и соавт. (1968), Л.Л. Шиком (1968). Суть его состоит в том, что при моделировании систему дыхания рассматривают не как изолированную, а во взаимосвязи с другими системами организма. Так, модель, описанная Б.В. Пет­ровским (1968), включает в себя системы кровообраще­ния, дыхания, тканевого обмена по нескольким веществам, систему регуляции сосудистого тонуса и др. Модель позволяет воспроизводить многие патологические эффек­ты, возможные в системах организма. Включенная в эту более общую модель, модель системы дыхания близка к модели [Horgan, 1968] в отношении зависимостей, опре­деляющих концентрации кислорода и СО₂ в артериальной крови, и задана системой уравнений, в которой три урав­нения задают условия переноса кислорода кровью, ис­пользуя кусочно-линейную аппроксимацию кривой диссо­циации гемоглобина. Они учитывают распределение кровотока по различным органам. Еще два уравнения влияют на развитие материального баланса для легких.

Все рассмотренные модели системы дыхания представ­ляют легкие, как жесткую емкость, через которую воздух протекает со скоростью, определяемой химическим соста­вом крови. Ни в одной из моделей не сделано попытки учесть отдельные фазы дыхательного и сердечного циклов. В более простых моделях изучение динамики СО₂ сводит­ся к изучению массообмена между «резервуарами» для СО₂; в более развитых моделях система дыхания явля­ется частью комплекса, охватывающего несколько систем организма. Во многих моделях влиянием О₂ и рН кро­ви на управление дыханием пренебрегают, сводя его к влиянию Рсо₂, и, несмотря на это, получают удовлетво­рительные результаты. Некоторые важные физиологиче­ские эффекты (например, влияние Рсо₂ на кривую диссо­циации оксигемоглобина) не учтены ни в одной из упомя­нутых моделей. Индивидуальные значения физиологических констант, от которых зависит поведение модели, мо­гут быть учтены только в результате изучения каждого конкретною организма. Последнее осложняет проверку адекватности модели и снижает ее ценность для решения задачи управления.

Главными трудностями при рассмотрении ИВЛ с точ­ки зрения управления являются изменяемость парамет­ров исследуемого объекта, их взаимосвязанность, а так­же нелинейный характер связей между переменными. При этом синтез системы автоматического управления наталкивается еще и на ограничения в выборе величины и ви­да управляющего воздействия, т.е. величины и скорости изменения вентиляции. В настоящее время намечаются два пути преодоления упомянутых трудностей.

Первый путь — принятие большого количества упро­щающих допущений и пренебрежение некоторыми свойст­вами объекта, обусловленное стремлением получить мо­дель, пригодную для реализации системы управления. В ряде задач, относящихся к биологическим объектам, это приводит к тому, что остаются неучтенными сущест­венные свойства объекта. Поэтому системы управления, построенные на основании таких моделей, в некоторых случаях не справляются с возложенными на них задачами [Сомс М.К. и др., 1962; Frumin, 1959; Rentsch, 1966].

Второй путь — усложнение модели, обусловленное стрем­лением к возможно более точному учету всех связей в объекте для достижения наибольшей адекватности. Это часто приводит к тому, что синтез управления на основе полученной модели существующими средствами теории управления становится затруднительным, а в некоторых случаях и невозможным [Алсксандер Д.М. и др., 1968; Гродниз Ф.С., 1966; Horgan, 1968].

Существуют, однако, другие возможности моделирова­ния биологического объекта, которые в явной форме не требуют выбора компромиссного решения между адекват­ностью модели и реализуемостью управления [Беллман Р., 1966]. Основная идея подобных методов заключается и сочетании статистических и детерминистских методов моделирования биологических объектов.

Одним из вариантов такого подхода является представ­ление объекта линейным дифференциальным уравнением со случайными коэффициентами, заданными своими зако­нами распределения [Бурлаков Р.П., Юшкин А.В., 1970]. Такой подход не игнорирует неизвестные свойства моде­лирующего объекта, в частности нелинейность и зависи­мость параметров объекта от неизвестных исследователю причин или от влияния одних параметров на другие. С другой стороны, на основе такой модели возможно ре­шить задачу синтеза управления, так как в настоящее вре­мя интенсивно разрабатываются методы построения си­стем управления, малочувствительных к изменению в из­вестных пределах параметров объекта [Нмельяиов В., 1967; Петров Б., 1968]. К недостаткам такого подхода следует отнести то, что модель в меньшей степени спо­собствует пониманию свойств объекта, чем, скажем, мо­дель, построенная по принципу усложнения уравнений.

В связи с изложенным нам представляется целесообраз­ным при моделировании процесса ИВЛ для решения за­дачи управления использовать идею описания объекта ли­нейным дифференциальным уравненном со статистически заданными коэффициентами.

Все изложенное выше в основном определило то об­стоятельство, что при моделировании ИВЛ мы описывали объект линейным дифференцнальным уравнением, коэф­фициенты которого заданы законами распределения.

Построение такого рода полустохастнчсской модели, имея ряд преимуществ, требует наличия и обработки боль­шого количества экспериментального материала.

Модель канала вентиляции —Рсо₂при ИВЛ. Было аппроксимировано 100 кривых Iэ=Рсоз (t), полученных вэксперименте на животных, и 107 экспериментальных кри­вых, полученных при ИВЛ у людей во время оператив­ного вмешательства по различным поводам. По результатам аппроксимации были построены гистограммы для коэффициентов дифференциального уравнения.

Здесь уместно привести основные допущения, при кото­рых модель можно считать адекватной объекту, а систе­ма управления, построенная на основании этой модели, будет обеспечивать заданное качество. Первое из этих до­пущений касается физиологической стороны отбора инфор­мации и предполагает соответствие (приближенное ра­венство) альвеолярного и артериального Рсо₂. При воз­никновении патологии, приводящей к нарушению этого соответствия в зависимости от вида патологии, система будет поддерживать Рсо₂, не соответствующее заданию, либо вообще окажется неработоспособной.

Второе допущение предполагает, что модель может отразить то изменение Рсо₂, которое может быть ском­пенсировано изменением минутной вентиляции. Точно так же и система управления может отработать лишь такое отклонение Pco₂. которое в состоянии скомпенсировать соответствующим изменением минутной вентиляции.

Третье допущение предполагает, что за время переход­ного процесса изменением коэффициентов дифференци­ального уравнения, описывающего объект, можно прене­бречь. Следует отметить, что это допущение в неявной форме предполагает кусочно-линейную линеаризацию ста­тической характеристики объекта.

О моделировании влияния ИВЛ на гемодинамику. По­скольку условия работы системы кровообращения при ИВЛ значительно отличаются от условий самостоятель­ного дыхания, то при выборе режима вентиляции необхо­димо уменьшить, насколько это возможно, вредное влия­ние ИВЛ на гемодинамику пациента. С другой стороны, полученная выше модель канала вентиляция — Рсо₂, да­вая возможность выбирать лишь величину вентиляции, оставляет произвольным способ ее задания. Приведенные выше данные о том, что система регуляции спонтанного дыхания задает способ вентиляции из условия минимума энергетических затрат на дыхание, при ИВЛ вряд ли сле­дует использовать, так как здесь расходуется энергия внешних источников.

Применяя известные модели системы кровообращения и дыхания, Бабский Е.Б. (1947), Петровский Б.В. (1968), Гайтон А. (1969), Horgan (1968) преобразовали блок-схе­му объекта в такой вид, чтобы в ней были учтены полу­ченные нами экспериментальные факты влияния ИВЛ на параметры гемодинамики (рис. 23). Блок V_D отражает наличие объема мертвого пространства и в соответствии с вышеприведенным выражением преобразует общую ми­нутную вентиляцию в альвеолярную. Блоки V_D и «диф­фузия» характеризуют модель ИВЛ, отражающую влия­ние вентиляции на артериальное Рсо₂.

Блок Р_т отражает возникновение давления в трахее (Рт) в результате вдувания определенного дыхательного объема Vt в легкие:

Рт =К'•С•V_T+ К"•R• dV_T/d•t

где С и R — соответственно растяжимость грудной клетки и легких и сопротивление дыхательных путей.

Блоки «Кровоток в легких», Pnii — давление в правом предсердии и Кмк — сопротивление в малом круге крово­обращения отражают влияние ИВЛ через Рт на гемо­динамику.

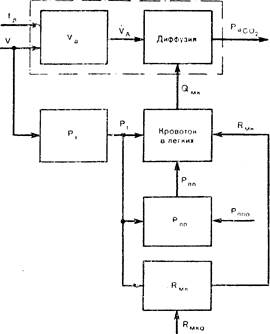
23. Блок-схема модели ИВЛ с учетом влияния режима ИВЛ на гемодннамнку. Объяснение в тексте.

Использование этой блок-схемы при синтезе системы управления ИВЛ требует прежде всего достаточного экс­периментального материала для аппроксимации переда­точных функций блоков конкретными зависимостями с численно заданными коэффициентами. При этом следует помнить, что необходимо выявить «критерий невмеша­тельства в гемодинамику» пациента, что является больше медицинской, чем технической, задачей. Однако для того чтобы уменьшить отклонения параметров гемодинамики от физиологических норм, т.е. направить процесс управ­ления ИВЛ в желаемом направлении, достаточно качест­венно рассмотреть предложенную модель. Ясно, что, уменьшая дыхательный объем, можно уменьшить и от­клонения от физиологических норм и параметров гемоди­намики. Наименьшую величину дыхательного объема в этом случае будет определять объем мертвого простран­ства.

Не следует забывать, что понятие мертвого пространст­ва в физиологии дыхания не ограничивается определением какого-либо объема легких, не участвующего в газообме не. На величину Vd влияют неравномерность вентиляции по отношению к кровотоку, нарушения диффузии и др. Измерение функциональной величины Vd в условиях ИВЛ чрезвычайно затруднительно.

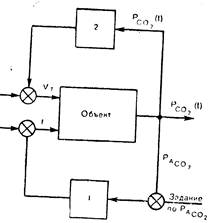
24. Блок-схема системы уп­равления ИВЛ с учетом уменьшения вредного влия­ния на гемодинамику. Объ­яснение в тексте:

1 — контур управления частотой дыхания по Рсо₂; 2 — устрой­ство управления дыхательным объемом с анализатором фор­мы капнограммы.

Для определения величины минимально допустимого объема дыхания при автоматически управляемой ИВЛ можно использовать капнограмму — кривую изменения концентрации СО₂ во время дыхательного цикла. Известно, что наличие горизонтального участка капнограммы в конце выдоха свидетельствует о достаточном промывании мертвого пространства и, кроме того, дает информацию о значении Рсо₂ в альвеолярном газе при отсутствии соот­ветствующих патологий.

Таким образом, можно представить следующую блок-схему системы управления ИВЛ (рис. 24), уменьшающей вредное влияние ИВЛ на гемодинамику пациента. Устрой­ство 2, анализирующее форму капнограммы Pco₂ (t). дис­кретно уменьшает дыхательный объем, пока кривая Рсо₂ имеет плато в конце выдоха и увеличивает его, если плато отсутствует, воздействуя тем самым на быстродействую­щий контур управления 1 частотой дыхания по Рсо₂. Контур 1, отработав это возмущение, установит новое значе­ние f, соответствующее заданному значению Рсо2, после чего устройство 2 вновь анализирует форму капнограм­мы. Этот процесс длится до тех пор, пока при заданном Рсо₂ минутная вентиляция будет осуществляться с ми­нимальным, но достаточным для получения значения Рсо₂ дыхательным объемом и соответственно увеличенной ча­стотой дыхания.

АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ ИСКУССТВЕННОЙ ВЕНТИЛЯЦИЕЙ ЛЕГКИХ С ИСПОЛЬЗОВАНИЕМ БИОЛОГИЧЕСКОЙ ИНФОРМАЦИИ

Практически все известные аппараты ИВЛ с автома­тическим управлением на основе использования биологи­ческой информации построены по принципу стабилизации заданного значения Pco₂. И медицинские специалисты, и инженеры являются сторонниками построения таких си­стем автоматического управления, которые в возможно большей степени заменяли бы утраченные по различным причинам функции систем организма, управляющих са­мостоятельным дыханием в нормальных условиях.

Существует по крайней мере две причины, которые за­трудняют решение этой проблемы. Первая из них состоит в том, что современные знания о системе дыхания и ме­тоды автоматического управления и отбора информации для его осуществления пока не позволяют еще решать та­кие задачи. Вторая и главная причина состоит в том, что патологические состояния, вынуждающие переходить на искусственную вентиляцию легких, чрезвычайно разнооб­разны. Воздействия же, которыми создатели аппаратуры располагают при искусственной вентиляции легких, определяются величинами ряда параметров вентиляции и воз­можностями изменения состава газовой смеси. Поэтому и постановка задачи автоматического управления ИВЛ име­ет смысл, когда имеющиеся в распоряжении методы воз­действия в состоянии оказать влияние на необходимые параметры организма в нужном направлении. Другими словами, управление функциями организма во время анесте­зиологического и реанимационного пособия значительно шире и разнообразнее воздействий, оказываемых на орга­низм самыми совершенными методами ИВЛ.

Несмотря на изложенное выше, проблема автоматиза­ции процесса ИВЛ остается весьма актуальной уже по­тому, что ее решение снимает с врача часть сложных за­дач, которые ему приходится решать в ходе анестезиоло­гических и реанимационных мероприятий.

Одна из систем управления ИВЛ по содержанию СО₂ в альвеолярном или выдыхаемом газе реализована в ап­парате ИВЛ РОА-1 [Сомс М.К. и др., 1962].

При проектировании этой системы авторы считали ста­тическую характеристику пациента в рабочем диапазоне линейной:

Pco₂ = f(v)

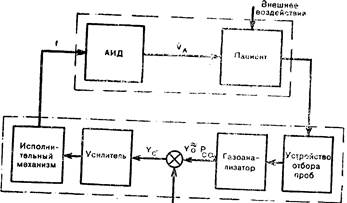
25. Блок-схема аппарата РОА-1. Объяснение в тексте.

Эта система (рис. 25) состоит из объекта управления с данной статической характеристикой управляющей систе­мы, включающей сравнивающе-задающее устройство, уси­литель, исполнительный механизм, устройство для получе­ния пробы альвеолярного газа и оптико-акустический га­зоанализатор.

Величина альвеолярного Pco₂, которую врач считает не­обходимым поддерживать у больного, задается при помо­щи сравнивающе-задающего устройства. Оно сравнивает сигнал задания Yi (заданное значение Р_Aсо₂) с сигналом газоанализатора Y₀ (фактическое значение Р_Aсо₂) и вы­рабатывает сигнал ошибки: Yc, (сигнал рассогласования):

Yc=Yi-Y₀

Сигнал ошибки подается на магнитный усилитель, кото­рый в зависимости от знака и величины Yc преобразовы­вает его в переменное напряжение с различной амплиту­дой и фазой. Это напряжение определяет скорость и на­правление вращения исполнительного механизма, который вращает элемент, задающий значение вентиляции на ап­парате искусственного дыхания. В этом аппарате вентиля­ция регулируется путем автоматического изменения часто­ты дыхания, а дыхательный объем устанавливается вруч­ную один раз на весь процесс регулирования.

Система управления аппарата РОА-1 реализует инте­гральный закон управления за счет применения в качестве исполнительного механизма реверсивного двигателя, управляемого магнитным усилителем, на вход которого подан сигнал рассогласования между заданной и изме­ряемой величинами Рсо₂ в альвеолярном газе.

Так как отбор пробы артериальной крови — процедура достаточно сложная и далеко не всегда необходима во время ИВЛ, то в этом аппарате, как и в других известных системах управления ИВЛ по Рсо₂ вместо Рсо₂ в артери­альной крови используется Рсо₂ в альвеолярном газе. У больных с отсутствием патологической неравномерности распределения вентиляции относительно легочного кровотока и с отсутствием значительного артериально-венозного шунта величина альвеолярного Рсо₂ находится в соответствии с величиной артериального Рсоз и ниже ее на 1 — 3 мм рт. ст. Это объясняется тем, что обмен углекис­лоты между кровью и альвеолами происходит очень быст­ро и при очень небольших градиентах напряжения СО2.

Такой прием позволяет применить в системе управления в качестве измерительного устройства обычный оптико-акустический газоанализатор, снабженный устройством отбора пробы, которое обеспечивает поступление в газо­анализатор смеси из последней трети объема выдоха. При этом считается, что дыхательный объем всегда установлен врачом таким, что к моменту наступления последней тре­ти выдоха мертвое пространство уже «промыто», и через устройство отбора проходит газ, концентрация СО2 в ко­тором равновесна с концентрацией Рсо₂ в артериальной крови. Для синтеза системы управления принята модель объекта с постоянными коэффициентами, не учитывающая возможности изменения параметров объекта. Такая воз­можность при ИВЛ, однако, имеется и при переходе от одного пациента к другому, и при проведении ИВЛ у одно­го и того же пациента, состояние которого не однозначно.

Другой системой управления ИВЛ по Рсо₂ в артериаль­ной крови является аппарат Лейпцигского научно-техни­ческого центра «Медицинмеханик» [Rentsch, 1966]. В этой системе для управления используется измерение Рсо₂ в альвеолярном газе, измеряемое инфракрасным газоанали­затором. В системе «Медицинмеханик» применен пневма­тический регулятор, реализующий пропорциональный за­кон управления. Модель, по которой производится синтез системы управления, как и предыдущая, не учитывала возможности изменения параметров объекта. Проверка устойчивости и выбор между обеспечением устойчивости и уменьшением величины статической ошибки регулиро­вания производились экспериментально на модели легких.

Несмотря на то, что авторы этой разработки подчеркивали зависимость качества управления от постоянной вре­мени и времени запаздывания у больного, от мертвого про­странства аппарата и от уровня Рсо₂, при построении ап­парата «Медицинмеханик» эти особенности объекта не были учтены. Очевидно, что при работе с пациентом, ха­рактеристики которого могут изменяться, эта система мо­жет иметь и неудовлетворительные (например, неустой­чивые) процессы регулирования.

Система автоматического управления ИВЛ по Рсо₂ [Фрумин М.X., 1958; Frumin, 1959] предусматривает ус­тановку частоты дыхания вручную и снабжена интеграль­ным регулятором, управляющим дыхательным объемом в зависимости от уровня Рсо₂ в альвеолярном газе. При синтезе этой системы управления возможность изменения параметров управления объекта также не учитывалась.

Перечисленные системы построены по принципу управ­ления интенсивностью вентиляции легких на основе ис­пользования информации о Pco₂ в альвеолярном газе. Недостатком такого подхода является то, что при некото­рых видах патологии (например, увеличенном венозно-артериальном шунте или ярко выраженной неравномерности легочной вентиляции по отношению к кровотоку) системы автоматического управления ИВЛ с таким отбором ин­формации окажутся неработоспособными по причине значительного несоответствия величин альвеолярного Рсо₂ и артериального Рсо₂.

Работы ряда авторов [Дарбинян Т.М. и др., 1965, 1969; Чеботарь А.И., 1966; Юревнч В.М., 1966, 1967] показа­ли, однако, что в большинстве случаев Рсо₂ в пробе аль­веолярного газа соответствует Рсо₂ в артериальной крови и почти всегда ниже этой величины на 1 — 3 мм рт. ст. Поддержание артериального Рсо₂ при ИВЛ с такой точ­ностью вполне допустимо. Описанные системы автомати­ческого управления ИВЛ, дающие подобную точность под­держания Рсо₂ на модели легких при настройке, в ряде случаев не могли обеспечить се при работе системы ап­парат — пациент. Более того, наблюдались неустойчивые или очень затянутые процессы регулирования, вследствие того, что модели, по которым производился синтез всех этих систем управления, не учитывали возможности изме­нений параметров объекта, влияния чистого запаздыва­ния, ограничений управляющего воздействия, помех и др. Поэтому представляется важным, хотя бы с удовлетво­рительной для практики точностью, решить задачу, в ко­торой перечисленные выше осложняющие обстоятельства учтены в комплексе. В работе А.В. Юшкниа (1970) была показана возможность подобного решения при помощи комбинирования методов нелинейного программирования и метода статистических испытаний. Преимущества такого подхода состоят в том, что трудности решения задачи син­теза системы управления, осложненной запаздыванием, помехами, ограничениями и т.п., переносятся в область вопросов сходимости алгоритмических методов поиска экс­тремума, точности воспроизведения объекта методами сто­хастического моделирования, объема памяти машины, вре­мени решения задачи и т.д. В связи с этим при синтезе системы управления ИВЛ пришлось решать ряд вопросов, связанных с численной реализацией алгоритма, модели­рующего объект управления и управляющие устройства.

Моделирование системы автоматического регулирования.Блок-схема алгоритма, осуществляющего стохастическое моделирование контура объект — регулятор и поиск пара­метров устройства управления, представлена на рис. 26. Алгоритм представляет собой математическую модель объекта, охваченную контуром управления с введением не­обходимых ограничений и запаздывания. Вся эта схема охвачена алгоритмом поиска, предназначенным для вы­числения некоторого функционала качества управления с осреднением по множеству наборов параметров модели объекта и способным влиять на параметры управляю­щего устройства в направлении изменения функционала к его экстремальному значению.

Блок ГПЧ — генератор псевдослучайных чисел с равно­мерным законом распределения в диапазоне 0 — 1. Блоки T₁, Т₂, Т₃, К, А являются фильтрами законов распреде­ления, выдают последовательности случайных величин, т.е. коэффициенты дифференциального уравнения модели объекта при ИВЛ соответственно закону распределения каждой из них. Блок Т₁/Т₂ реализует дополнительную фильтрацию Т₂ и T₁ с целью воспроизведения корреляции между ними. Блоки W₁ (р) и W₂ (р) реализуют линейную часть модели ИВЛ. Все вышеуказанные блоки, кроме ГПЧ (пунктир), образуют модель канала вентиляция — Рсо₂ при ИВЛ.

Блок ограничений и управляющий блок моделируют уравнения контура управления с учетом ограничений пре­делов и скорости изменения минутной вентиляции.

Аппарат ИВЛ с автоматическим управле­нием, построенный на основе моделирования. Анализ результатов испытаний модели системы управления ИВЛ позволил построить аппарат ИВЛ (рис. 27) с использованием биологической информации для управления — РОА-2.

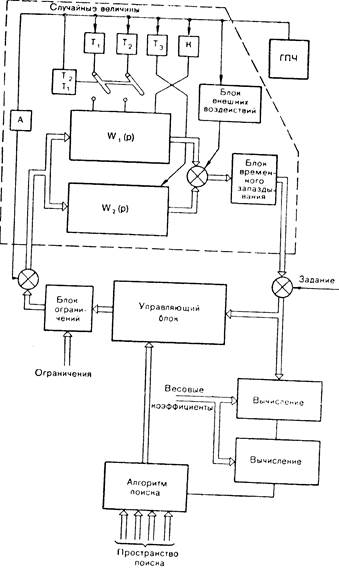
26. Блок-схема алгоритма моделирования системы управле­ния ИВЛ. Объяснение в тексте

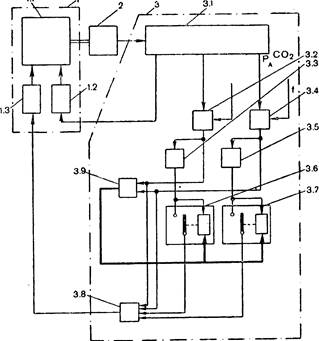
27. Блок-схема аппарата РОЛ-2. Объяснение в тексте.

Газовая смесь из блока искусственного дыхания 1 по­ступает в газоанализатор 2. Сигнал с выхода газоанали­затора (капнограмма) поступает в цифровую часть 3.1 блока регулирования 3, где вычисляется значение парци­ального давления углекислоты в альвеолярном газе Р_Асо₂, значение производной от Р_Асо₂ и определяется на­личие или отсутствие плато на каппограмме.

Контур управления дыхательным объемом 3.1, 1.2 ра­ботает следующим образом. При наличии на капнограмме плато цифровая часть блока регулирования 3.1 вырабаты­вает сигнал, который в течение следующего дыхательного цикла включает исполнительный механизм 1.2 в линии управления величиной дыхательного объема аппарата ИВЛ 1.1 в сторону уменьшения величины дыхательного объема; при отсутствии плато исполнительный механизм 1.2 увеличивает дыхательный объем. Таким образом, ве­личина дыхательного объема поддерживается иа мини­мально допустимом уровне, достаточном, чтобы промыть мертвое пространство пациента.

Остальная часть блок-схемы (см. рис. 27) образует кон­тур управления величиной минутной вентиляции.

Сигнал, соответствующий значению Р_Асо₂, поступает на операционный усилитель 3.4, где сравнивается с заданным уровнем Р_Асо₂. Рассогласование между заданным и те­кущим значением Р_Асо₂; (X₁), а также производная от это­го рассогласования (Х₂), получаемая на выходе опера­ционного усилителя 3.2 после вычитания постоянной со­ставляющей, используется для управления величиной минутной вентиляции в сети переменной структуры, образо­ванной операционными усилителями 3.3 и 3.5, обеспечи­вающими инвертирование рассогласования X₁ и производ­ной X₂; сумматорами 3.8 и 3.9; блоками знака произве­дения 3.6 и 3.7, обеспечивающими коммутацию сигналов инверторов 3.3 и 3.5 на вход сумматора 3.8 в зависимости от знака произведения входных сигналов на их входах.

Управляющее воздействие, получаемое на выходе опера­ционного усилителя 3.8, отрабатывается исполнительным механизмом 1.3 в линии управления величиной минутной вентиляции блока ИВЛ.

Значения коэффициентов усиления в операционных уси­лителях, образующих управляемую сеть переменной струк­туры, выбраны таким образом, что при изменении харак­теристик объекта во всем диапазоне в системе возникает скользящий режим, обеспечивающий независимость качества управления величиной минутной вентиляции от ха­рактеристик объекта управления.

Опыт клинического применения аппаратов РОА-2 пока­зал безусловную необходимость развития этого направле­ния техники на основе углубления знаний в первую оче­редь о самом процессе ИВЛ, его биологических особенно­стях. Одновременно была реализована идея снижения влияния ИВЛ на гемодинамику за счет уменьшения дыха­тельного объема и повышения частоты дыхания, вызываю­щая в настоящее время большой интерес у клиницистов.